LCA --- 常规的三种算法
模板题,后面的三种方法都可以做,模板也是基于这道题的
最常用的就是倍增:
1:LCA – 倍增(在线算法)比RMQ和tarjan算法都好写, 并且复杂度不高, 预处理nlogn, 询问logn.
up[i][j] 代表i的第2^j个祖先是谁. maxx[i][j] 表示i到其第2^j个祖先的路径上的最大值.
那么询问树上任意两点之间路径的最大值就可以在logn的时间内求出来.
模板:
const int maxn = 1e5 + 5;
int up[maxn][23], maxx[maxn][23];
int dep[maxn], dis[maxn];
int cnt, head[maxn];
int n, m, q;
struct node {
int to, next, w;
}e[maxn<<1];
void init() {
Fill(head,-1); Fill(dis,0);
Fill(up,0); Fill(dep,0);
cnt = 0; Fill(maxx, 0);
}
void add(int u, int v, int w) {
e[cnt] = node{v, head[u], w};
head[u] = cnt++;
}
void dfs(int u,int fa,int d) {
dep[u] = d + 1;
for(int i = 1 ; i < 20 ; i ++) {
up[u][i] = up[up[u][i-1]][i-1];
// maxx[u][i] = max(maxx[up[u][i-1]][i-1], maxx[u][i-1]);
}
for(int i = head[u] ; ~i ; i = e[i].next) {
int to = e[i].to;
if(to == fa) continue;
dis[to] = dis[u] + e[i].w;
up[to][0] = u;
// maxx[to][0] = e[i].w;
dfs(to, u, d+1);
}
}
int LCA_BZ(int u,int v) {
int mx = 0;
if(dep[u] < dep[v]) swap(u,v);
int k = dep[u] - dep[v];
for(int i = 19 ; i >= 0 ; i --) {
if((1<// mx = max(mx, maxx[u][i]);
u = up[u][i];
}
}
if(u == v) return u;
for(int i = 19 ; i >= 0 ; i --) {
if(up[u][i] != up[v][i]){
// mx = max(mx, maxx[u][i]);
// mx = max(mx, maxx[v][i]);
u = up[u][i];
v = up[v][i];
}
}
// return max(mx, max(maxx[u][0], maxx[v][0]));
return up[u][0];
}
int kth(int u, int v, int k) { // 算u到v的路径的第k个结点.
--k; int f = LCA_BZ(u, v);
if (dep[u] - dep[f] < k) {
k = dep[v] - dep[f] - k + dep[u] - dep[f];
swap(u, v);
}
for (int i = 19 ; i >= 0 ; i --) {
if (k & (1 << i)) u = up[u][i];
}
return u;
}
void solve() {
scanf("%d%d",&n,&m);
init();
for(int i = 1 ; i < n ; i ++) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
add(u, v, w); add(v, u, w);
}
//maxx[1][0] = 0;
dfs(1, -1, 0);
while(m--) {
int u, v;
scanf("%d%d",&u, &v);
int res = dis[u] + dis[v] - 2 * dis[LCA_BZ(u,v)];
printf("%d\n", res);
}
} //理解离线算法的核心: 在dfs过程中, 一定会遍历到每两个点的的LCA, 并且由于顺序问题, 一定不会遍历到他们的LCA的祖先, 所以就可以当遍历到第二个相关的点时就可以直接求出了他们LCA了.
tarjan离线这篇博客讲的很好
2: LCA – tarjan 算法 (离线算法), 是把所有询问都存下来, 一次性回答完, 比较好懂, 复杂度O(n+q),就是麻烦再要把答案排好序输出. 其他的还好.
有什么不懂的地方看看那篇博客.
@@@模板
const int maxn=1e5+5;
int head_node[maxn],head_query[maxn];
bool vis[maxn];
int dis[maxn],pre[maxn];
int cnt_node,cnt_query;
int n,m;
struct node
{
int to,next,w;
}s[maxn*2];
struct query
{
int u,to,next,lca;
}ans[maxn*10];
int Find(int x)
{
return pre[x] == x ? x : pre[x] = Find(pre[x]);
}
void Un(int u,int v)
{
u = Find(u);
v = Find(v);
if(u != v)
pre[v] = u;
}
void init()
{
Fill(head_node,-1);
Fill(head_query,-1);
Fill(vis,false);
Fill(dis,0);Fill(s,0); Fill(ans,0);
for(int i=1;i<=n;i++)
pre[i] = i;
cnt_node = cnt_query = 0;
}
void add_node(int u,int v,int w)
{
s[cnt_node].to = v;
s[cnt_node].w = w;
s[cnt_node].next = head_node[u];
head_node[u] = cnt_node++;
}
void add_query(int u,int v)
{
ans[cnt_query].u = u;
ans[cnt_query].to = v;
ans[cnt_query].next = head_query[u];
head_query[u] = cnt_query++;
}
void tarjan(int u)
{
vis[u] = true;
for(int i=head_node[u]; ~i; i = s[i].next){
int v = s[i].to;
int w = s[i].w;
if(!vis[v]){
dis[v] = dis[u] + w;
tarjan(v);
Un(u,v);
}
}
for(int i=head_query[u]; ~i ; i = ans[i].next){
int v = ans[i].to;
if(vis[v]){
ans[i].lca = ans[i^1].lca = Find(v);
}
}
}
void solve()
{
scanf("%d%d",&n,&m);
init();
for(int i=0;i1;i++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
add_node(u,v,w);
add_node(v,u,w);
}
for(int i=0;i<m;i++){
int u,v;
scanf("%d%d",&u,&v);
add_query(u,v);
add_query(v,u);
}
tarjan(1);
for(int i=0;i2){
int res = dis[ans[i].u] + dis[ans[i].to] - 2 * dis[ans[i].lca];
printf("%d\n",res);
}
} !!!解释版
const int maxn=1e5+5;
int head_node[maxn],head_query[maxn];
bool vis[maxn];
int dis[maxn],pre[maxn];
int cnt_node,cnt_query;
int n,m;
struct node
{
int to,next,w;
}s[maxn*2];
struct query
{
int u,to,next,lca;
}ans[maxn*10];
int Find(int x) //并查集.
{
return pre[x] == x ? x : pre[x] = Find(pre[x]);
}
void Un(int u,int v)
{
u = Find(u);
v = Find(v);
if(u != v)
pre[v] = u;
}
void init()
{
Fill(head_node,-1);
Fill(head_query,-1);
Fill(vis,false);
Fill(dis,0);Fill(s,0); Fill(ans,0);
for(int i=1;i<=n;i++)
pre[i] = i;
cnt_node = cnt_query = 0;
}
void add_node(int u,int v,int w) //建立搜索边.
{
s[cnt_node].to = v;
s[cnt_node].w = w;
s[cnt_node].next = head_node[u];
head_node[u] = cnt_node++;
}
void add_query(int u,int v) //建立答案边.
{
ans[cnt_query].u = u;
ans[cnt_query].to = v;
ans[cnt_query].next = head_query[u];
head_query[u] = cnt_query++;
}
void tarjan(int u)
{
vis[u] = true;
for(int i=head_node[u]; ~i; i = s[i].next){
int v = s[i].to;
int w = s[i].w;
if(!vis[v]){
dis[v] = dis[u] + w;
tarjan(v);
Un(u,v); //表示v的爸爸的是u.
}
}
for(int i=head_query[u]; ~i ; i = ans[i].next){ //check每一个询问,看是否可以回答.
int v = ans[i].to;
if(vis[v]){
ans[i].lca = ans[i^1].lca = Find(v);
//因为存的时候相关的边时挨着存的,也就是^1的关系.
}
}
}
void solve()
{
scanf("%d%d",&n,&m);
init();
for(int i=0;i1;i++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
add_node(u,v,w); //双向边
add_node(v,u,w);
}
for(int i=0;iint u,v;
scanf("%d%d",&u,&v);
add_query(u,v); //存询问.方便一次性全部输出答案.
add_query(v,u);
}
tarjan(1);
for(int i=0;i2){
int res = dis[ans[i].u] + dis[ans[i].to] - 2 * dis[ans[i].lca];
printf("%d\n",res);
}
} ST在线这篇博客讲的很好
3: LCA-RMQ 在线算法(即问一个答一个)借用上面那张图(一般不用)
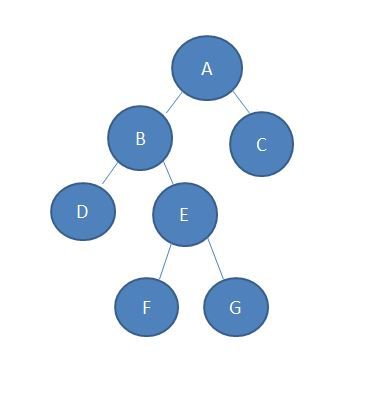

看完这幅图, 我觉得你就应该懂了. 给出代码实现: (注意不是很懂某些地方为什么处理时, 请看看那篇我推荐的博客和解释版) 关键在于如何充分利用深度与遍历序列下标的关系!!! 因为深度所对应的位置的pre就是我们要求的那个点.
@@@模板
const int maxn=4e4+5;
int head[maxn], first[maxn] ;
int pre[2*maxn], deep[2*maxn];
int dis[maxn];
int dp[maxn*2][25];
bool vis[maxn];
int n,m;
int cnt,tot;
struct node
{
int to,next,w;
}s[maxn*2];
void init()
{
Fill(vis,false); Fill(head,-1);
Fill(first,0); Fill(dp,0);
Fill(deep,0); Fill(pre,0);
cnt = tot = 0;
}
void add(int u,int v,int w)
{
s[cnt].to = v;
s[cnt].w = w;
s[cnt].next = head[u];
head[u] = cnt++;
}
void dfs(int u,int dep)
{
vis[u] = true; pre[++tot] = u;
first[u] = tot; deep[tot] = dep;
for(int i=head[u] ; ~i ; i=s[i].next){
int v = s[i].to; int w = s[i].w;
if(!vis[v]){
dis[v] = dis[u] + w;
dfs(v,dep+1);
pre[++tot] = u;
deep[tot] = dep;
}
}
}
void RMQ_ST(int len)
{
for(int i=1;i<=len;i++)
dp[i][0] = i;
for(int j=1;(1<for(int i=1;i+(1<1<=len;i++){
int a = dp[i][j-1] , b = dp[i+(1<<(j-1))][j-1];
dp[i][j] = deep[a] < deep[b] ? a : b ;
}
}
}
int Find(int l,int r)
{
int k = log2(r-l+1);
int a = dp[l][k], b = dp[r-(1<1][k];
return deep[a] < deep[b] ? a : b ;
}
int LCA(int u,int v)
{
int x = first[u], y = first[v];
if(x > y) swap(x,y);
int res = Find(x,y);
return pre[res];
}
void solve()
{
init();
scanf("%d%d",&n,&m);
for(int i=1;iint u,v,w;
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
add(v,u,w);
}
dfs(1,1);
RMQ_ST(2*n-1);
while(m--){
int u,v;
scanf("%d%d",&u,&v);
int res = dis[u] + dis[v] - 2*dis[LCA(u,v)];
printf("%d\n",res);
}
} !!!解释版
const int maxn=4e4+5;
int head[maxn], first[maxn] ;
int pre[2*maxn], deep[2*maxn]; //pre保存的是遍历的节点序列.deep是对应pre的每一个节点所在的深度.
int dis[maxn];
int dp[maxn*2][25]; //保存的信息是最小深度的位置关系了,这样才方便查询.
bool vis[maxn];
int n,m;
int cnt,tot;
struct node //存边的信息.
{
int to,next,w;
}s[maxn*2];
void init()
{
Fill(vis,false); Fill(head,-1);
Fill(first,0); Fill(dp,0);
Fill(deep,0); Fill(pre,0);
cnt = tot = 0;
}
void add(int u,int v,int w)
{
s[cnt].to = v;
s[cnt].w = w;
s[cnt].next = head[u];
head[u] = cnt++;
}
void dfs(int u,int dep) //遍历这棵树
{
vis[u] = true; pre[++tot] = u; //记下每一个对应的pos.
first[u] = tot; deep[tot] = dep;
for(int i=head[u] ; ~i ; i=s[i].next){
int v = s[i].to; int w = s[i].w;
if(!vis[v]){
dis[v] = dis[u] + w;
dfs(v,dep+1);
pre[++tot] = u;
deep[tot] = dep;
}
}
}
void RMQ_ST(int len) //len就是最长dfs遍历的长度,就是2*n-1.
{
for(int i=1;i<=len;i++) //存的是遍历的序列,后面更新时是把dp更新成了deep的位置,即tot,
dp[i][0] = i; //所以越往后面dp就是求的位置区间的一个最小值,也就是我们所要求的.
for(int j=1;(1<for(int i=1;i+(1<1<=len;i++){
int a = dp[i][j-1] , b = dp[i+(1<<(j-1))][j-1];
dp[i][j] = deep[a] < deep[b] ? a : b ;
}
}
}
int Find(int l,int r) //这个询问仅仅是返回一个位置,即LCA所在序列数组的位置,pre[res]才是LCA的标号
{
int k = log2(r-l+1);
int a = dp[l][k], b = dp[r-(1<1][k]; //保存的是编号,因为deep与pre数组同时保存了深度和编号
//所以可以通过直接返回放回对应深度的位置就行了, 不懂的话请具体看看那幅图.
// printf("@@@@%d %d %d %d\n",deep[a],deep[b],a,b);
return deep[a] < deep[b] ? a : b ;
}
int LCA(int u,int v) //求u,v的LCA.
{
int x = first[u], y = first[v];
if(x > y) swap(x,y);
int res = Find(x,y);
return pre[res];
}
void solve()
{
init();
scanf("%d%d",&n,&m);
for(int i=1;iint u,v,w;
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
add(v,u,w);
}
dfs(1,1);
RMQ_ST(2*n-1);
while(m--){
int u,v;
scanf("%d%d",&u,&v);
int res = dis[u] + dis[v] - 2*dis[LCA(u,v)];
printf("%d\n",res);
}
}