一道好题：机房小测-Tarjan判断必经点

转自 http://blog.csdn.net/izumi_hanako/article/details/78376731

说在前面

没什么好说的=w=（但是要保持格式）

---

题目

（原样例实在是太水了,我自己出了几组，在程序末尾）

---

解法

一个很经典的模型：”一张无向图从1走到N的必经点”
考试的时候写出来的程序在逻辑上有点问题，不过me的代码自带容错性，卡不掉的hhhhhh。不过还是决定把这个问题记录下来，以后方便复习。

可以发现，必经点一定是1到N路径上的某一个点（路径上每个点只能经过一次，不能1->u->v->u->N），me称之为路径点。那么只需要将所有这样的点先用一边dfs标记出来，然后再跑一遍tarjan求割点就好了。
相当于是要把图上的”枝丫点”给撇开不管，找剩下的图中的割点。

然而这样的”路径点”并不能用像下面这样的dfs去预处理：

bool acc[100005] ;
void dfs_acc( int u , int f ){
    if( u == N ) acc[u] = true ;
    for( int i = head[u] ; i ; i = p[i].pre ){
        int v = p[i].to ;
        if( v == f ) continue ;
        dfs_acc( v , u ) ;
        acc[u] |= acc[v] ;
    }
}

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10

这个dfs的思路很简单，却存在漏洞。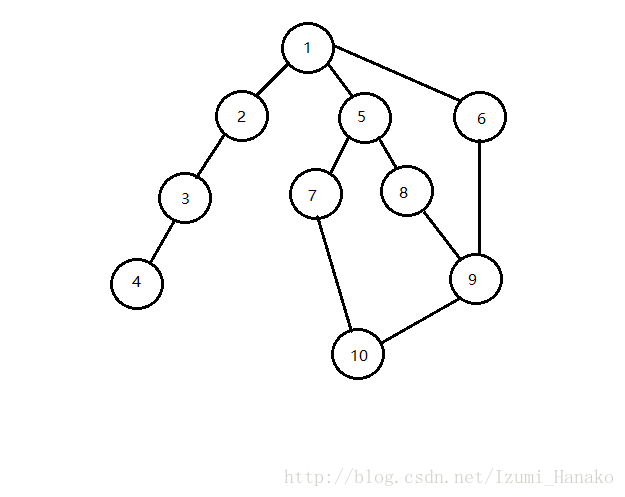

因为dfs是有先后顺序的。比如上面这个图，dfs顺序可能如下：
1->5->8->9->6->1->return，如果在9号节点先进入的是6号节点，那么6号节点就无法被标记为”路径点”。因此是无法先用一边dfs预处理的。

正确的做法是在tarjan的时候，无论点是不是路径点，都进去dfs一遍。如果在某一个u->v的时候有lowv ≥ dfn[u]，并且v可以到达N点，u才是必经点。正确性是显然的，如果是v导致了u被判为割点，并且v还能到N点，那么说明N一定在v的子树内。这种情况下，1点必须经过u点才能走到N，可以感性理解一下。

因此严谨的逻辑是：先判断割点，再看导致该点被判为割点的点是否是”路径点”，如果是，那么该点就是割点。
而不严谨的逻辑是：先判断该点是路径点，再跑tarjan求割点。（其实这个逻辑是对的，但是实现过程会出错）

---

自带大常数的代码

#include 
#include 
#include 
using namespace std ;

int T , N , M , tp , head[200005] , cnt ;
struct Path{
    int pre , to ;
}p[4*200005] ;

void In( int t1 , int t2 ){
    p[++tp].pre = head[t1] ;
    p[ head[t1] = tp ].to = t2 ;
}

inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}

bool iscut[200005] , acc[200005] ;
int dfn[200005] , dfs_c ;

int dfs( int u , int f ){
    int lowu = dfn[u] = ++dfs_c ;
    for( int i = head[u] ; i ; i = p[i].pre ){
        int v = p[i].to ;
        if( v == f ) continue ;
        if( !dfn[v] ){
            int lowv = dfs( v , u ) ;
            lowu = min( lowu , lowv ) ;
            if( lowv >= dfn[u] && acc[v] )
                iscut[u] = true ;
        } else lowu = min( dfn[v] , lowu ) ;
        acc[u] |= acc[v] ;
    }
    return lowu ;
}

void solve(){
    acc[N] = true ;
    dfs( 1 , 0 ) ;
    for( int i = 2 ; i < N ; i ++ )
        if( iscut[i] ) cnt ++ ;
    printf( "%d\n" , cnt ) ;
    for( int i = 2 ; i < N ; i ++ )
        if( iscut[i] ) printf( "%d " , i ) ;
    printf( "\n" ) ;
}

void clear(){
    dfs_c = tp = cnt = 0 ;
    memset( head , 0 , sizeof( head ) ) ;
    memset( dfn , 0 , sizeof( dfn ) ) ;
    memset( acc , false , sizeof( acc ) ) ;
    memset( iscut , false , sizeof( iscut ) ) ;
}

int main(){
    freopen( "home.in" , "r" , stdin ) ;
    freopen( "home.out", "w" , stdout) ;
    T=read();
    while( T -- ){
        clear() ;
        N=read(),M=read();
        for( int i = 1 , u , v ; i <= M ; i ++ ){
            u=read(),v=read();
            In( u , v ) ; In( v , u ) ;
        }
        solve() ;
    }
    return 0 ;
}

/*
5
4 3
1 2
2 3
3 4

5 5
1 2
2 3
3 4
4 5
4 1

20 22
1 2
2 3
2 4
3 5
3 6
4 7
4 8
5 9
9 10
8 11
11 12
5 13
5 14
6 14
7 15
8 15
8 16
13 17
14 18
15 18
16 19
18 20

5 5
1 2
2 3
3 5
1 4
4 5

5 5
1 2
2 3
3 4
4 5
4 1
*/

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43
• 44
• 45
• 46
• 47
• 48
• 49
• 50
• 51
• 52
• 53
• 54
• 55
• 56
• 57
• 58
• 59
• 60
• 61
• 62
• 63
• 64
• 65
• 66
• 67
• 68
• 69
• 70
• 71
• 72
• 73
• 74
• 75
• 76
• 77
• 78
• 79
• 80
• 81
• 82
• 83
• 84
• 85
• 86
• 87
• 88
• 89
• 90
• 91
• 92
• 93
• 94
• 95
• 96
• 97
• 98
• 99
• 100
• 101
• 102
• 103
• 104
• 105
• 106
• 107
• 108
• 109
• 110
• 111
• 112
• 113
• 114
• 115
• 116
• 117
• 118
• 119
• 120
• 121
• 122
• 123
• 124
• 125
• 126
• 127
• 128
• 129
• 130