最小割常见模型
易知,根据最大流最小割定理,最小割就等于最大流的,所以遇到一些题目,
只需要把它转化成一种最小割的模型,然后就可以通过一些最大流算法来解决例如Dinic,ISAP等。这里就不详细讲这些算法了,
要是想了解算法也可以,这里给出地址
是关于Dinic算法的,
直接讲最小割的模型吧。
有很多模型可以通过最小割解决,这里主要讲以下几种,
其实二分图最大匹配只是一个铺垫,它并不属于最小割的模型,而是整个网络流的模型
还有一种是最大密度子图,由于比较复杂,作者暂时还没学会,所以以后补充:
- 二分图
- 最大匹配
- 最小点权覆盖
- 最大点权独立集
- 最大权闭合图
- 最大密度子图(暂不讲)
###一、二分图最大匹配
很多人可能都会用匈牙利算法来解决这类问题,
但其实也可以用网络流来做,不过还是重新讲回最大匹配的定义。
(要是会匈牙利的话就直接跳过这段叙述看后面吧)
二分图最大匹配是指给定一个二分图,
二分图意思就是给定两个集合的点,同一个集合的点没有相连的边,只有连向另一个集合的边。
形象的说就是有一个班,排成两队,左边是男生,右边的是女生,
老师开始异想天开,现在要进行排座位,
老师为了增强异性间的交流,想让更多的男生找到女同桌。
于是规定一些指定的男生可以和指定的女生坐(二分图中的边),没有指定的即是不允许。
二分图最大匹配的意思是,在这里即希望能让尽量多的男生找到女同桌。
此时男生个数即使最大匹配数。
例如说,现在这个班有三个男生,三个女生
(这只是假设,现实中不可能那么少人)
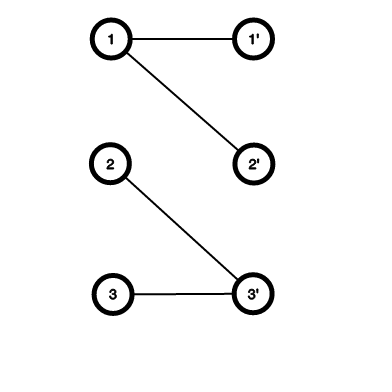
那么,以下的图表示的意思就是:(x代表男生,x’代表女生)
老师允许1号男生和1号或2号女生坐,2号男生可以和3号女生坐,3号男生也可以。
我们知道,最后排完之后,一个男生最多只可能和一个女生坐,一个女生最多也就只能和一个男生坐。
抽象的讲就是,最后两边的点最后只能选择一条边出去。
也就是1号男生只能在1号和2号女生里面选一个作为同桌,
3号女生只能在2号和3号男生里面的一个作为同桌。
这时,当1号男生选择1号女生,2号男生选择3号女生时,
满足最大匹配,此时匹配数为2(当然,还有很多情况也还满足)
我们知道,最大流意思是源点源源无尽地向有容量限制的水管(边)灌水,求汇点所能灌到水的最大数目。
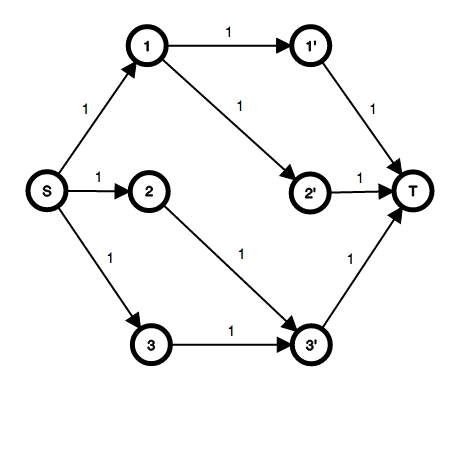
把最大匹配转化成最大流,这道题其实就是有很多个源点(男生),向汇点(女生)灌水,求最大流。
为了方便计算,我们要先把二分图内的无向边转化成有向边,表示从左边流到右边,权值为1,这样的话最大流就好算,直接就是二分图最大匹配个数。
####技巧I:多源点多汇点的问题,可以建立超级源点和汇点来解决
建立一个超级源点,源点连接左边,那么这个时候因为左边的点最后只能够选择一条边,所以此时源点到左边点的边权为1,>1的话即代表左边的点可以选择多条边流过去。
例如为3的话,因为二分图原来的连线权值为1,那么这个时候左边点(男生)可能会选择3个右边点(女生),这就变成二分图多重匹配了,是不合理的。
同理,右边点到汇点的边权也是1。
这样跑一遍最大流,所得的值就是二分图的最大匹配。
相关推荐题目:
1、poj 2446 ChessBoard
详细题解
简要思路:
黑白染色,黑色和白色的方格为二分图的两部分,
除了有障碍的之外,黑色的方格和相邻的白色方格相连。
填12的方格,即选择一条黑色和白色的方格的连边。
问最多放多少12,即是二分图最大匹配。
2.各种二分图最大匹配的题目……不一一列举
###二、二分图最小点权覆盖
这个的意思是,在二分图中的点都有一个权值,其中选定一些点,使这些点能够覆盖所有边,即满足所有边的其中一个点是选定点的一个,同时让点权的和尽量的小。
例如给定一个二分图:
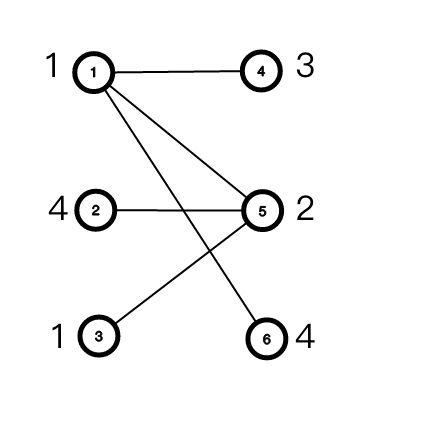
此时最好就是选择编号为1、5的点,最小点权覆盖即为1+2=3。
对于这种题目,我们一般把最小点权覆盖转化成最小割。
####技巧II:对于有点权限制的题目,可以转化成边权满足限制条件
所以构造源点,连接源点和左边的点,边权为该点的点权,汇点同理,原来相邻的点的边变成有向边,边权为inf
这样跑出来的最大流结果就是最小点权覆盖,详细证明如下:
我们知道如果存在最小割,那么任何形如S-u-v-T的线路上必定是不通的(即有割从中经过,否则不满足割的性质)
因为是求最小割,而u-v的边权是inf,因此割不会从此经过,也就是从
s-u,v-t中选一个经过。
选了一条边之后,边上除了源点和汇点的另外一个点即视为选中,
所以当有割时,任意一个s-u-v-t的线路肯定是u或者v被选中,
也就是满足所有边都覆盖。
当是最小割时,点权覆盖也为最小。
所以最小割=最小点权覆盖,
同时又最大流最小割定理可知,最大流=最小割,所以这类题目可以跑一下网络流最大流来完成。
###二分图最大点权独立集
最大点权独立集的定义是,在二分图中选定一些点,使这些点不被边直接相连的同时满足点权和最大。
其实,点权独立集与点权覆盖是恰好互补的。
意思即是点权独立集所选的点是所有点除了点权覆盖的点之外的点。
也就是独立集+覆盖集=总点权和,
所以独立集取max时,覆盖集为最小,
即最大点权独立集=所有点权和-最小点权覆盖,
按点权覆盖的那个图来说,
最大点权独立集即选点2、3、4、6,
等于4+1+3+4=12
证明如下:
证明独立集与覆盖集互补,
设图为G=(V,E),其中有一个点的集合V1和V2为V-V1,
V 1 , V 2 ⊆ V V1,V2 \subseteq V V1,V2⊆V
V1为覆盖集当且仅当V2为独立集
1、充分性:覆盖集=>独立集,
若V2不是独立集,即存在 u , v ∈ V 2 u,v \in V2 u,v∈V2,使得 ( u , v ) ∈ E (u,v) \in E (u,v)∈E,此时 u , v ∉ V 1 u,v \notin V1 u,v∈/V1,所以(u,v)这条边没有被覆盖集覆盖,矛盾。
2、必要性:独立集=>覆盖集,
若V1不是覆盖集,即存在 u , v ∉ V 1 u,v \notin V1 u,v∈/V1,也就是 u , v ∈ V 2 u,v \in V2 u,v∈V2,所以(u,v)这条边在独立集当中,矛盾
证毕.
一般这两类会放在一起,题目有很多:
1、Hdu 1569 方格取数(二)
简要思路:黑白染色然后直接求
2、Hdu 3820 Golden Eggs
简要思路:与上题,差不多,但一个方格有金、银两种状态,进阶版。
3、poj 3308 Paratroopers(好题!推荐)
简要思路:流只能相加,不能想乘,所以把a*b转化成exp(ln(a)+ln(b)),
也就是源点连接代表行的点,权值为ln(所需代价),汇点同理,
每有一个外星人,连接其所在行代表的点,和列代表的点。
最后求了最大流ans之后,输出exp(ans)即可。
注意:一个小细节,poj交G++时printf double要用"%f",C++用"%lf"
###最大权闭合图
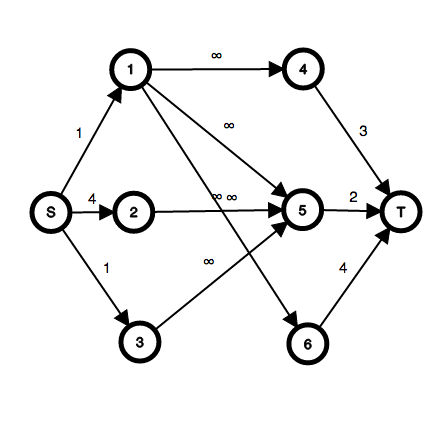
闭合图是指在图中选一个子图使得子图中点连出边的终点还在子图中。(也可以叫做闭包,译名不同)
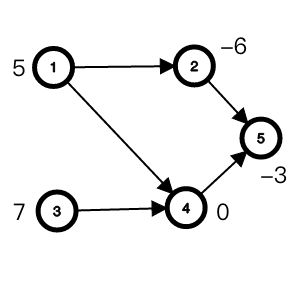
例如上图就有9个闭合图(含空集):∅,{3,4,5},{4,5},{5},{2,4,5},{2,5},{2,3,4,5},{1,2,4,5}和{1,2,3,4,5},
其中最大权闭合图**(可以叫做最大权闭包)**就是点权最大的闭合图是{3,4,5},权和为4。
对于求最大权闭合图,我们一般将其转化为最小割,
(把点权转化成边的限制的思路)
建立源点,汇点,把原图上边的权值改为无限大。
设简单割[S,T]将网络N的点集 V N V_{N} VN划分为点集 S S S及其补集
T ( T = V − S ) T (T=V −S) T(T=V−S),满足 s ∈ S , t ∈ T s∈S,t∈T s∈S,t∈T。设闭合图为 V 1 V_{1} V1,则它在 V V V中的补集为 V 2 ( V 2 = V − V 1 ) V_{2}(V_{2} =V−V_{1}) V2(V2=V−V1)。
记$V_{+} 为 为 为V$ 中点权为正的点集, V − V_{-} V− 为 V V V中点权为负的点集。
源点连 V + V+ V+的点, V − V- V−的点连汇点,边权为点权的绝对值。
此时最大权闭合图为 ∑ u ∈ V + \sum_{u\in V+} ∑u∈V+减去最小割的值,
等等会说明为什么。
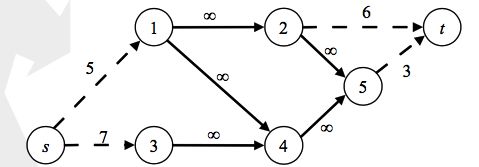
为什么呢?首先,建图把原图边的权值改为∞。
所以最小割只会经过源点和汇点连的边,即该最小割为简单割(简单割定义是割经过每条边都和源或汇关联)
但如何将闭合图和简单割一一对应呢?
1、充分性
即 S = V 1 ⋃ s , T = V 2 ⋃ t S=V_{1}\bigcup {s},T=V_{2}\bigcup {t} S=V1⋃s,T=V2⋃t,求证(S,T)构成简单割,
若不构成,即存在 u , v ∈ E u,v\in E u,v∈E,且 u ∈ S − { s } = V 1 , v ∈ T − { t } = V 2 u\in S-\{s\}=V_{1},v\in T-\{t\}=V_{2} u∈S−{s}=V1,v∈T−{t}=V2,使得(S,T)含不与源汇相连的边,此时闭合图有边(u,v)连到外面,不符合定义。所以(S,T)构成简单割
2、必要性
即证 V 1 = S − { s } V_{1}=S-\{s\} V1=S−{s}是闭合图。对于任意一条由 u ∈ V 1 u\in V_{1} u∈V1引出的边 ( u , v ) ∈ E (u,v)\in E (u,v)∈E,由于简单割[S,T]不含E中的任何边,故 v ∉ T − { t } = V 2 v\notin T-\{t\}=V_{2} v∈/T−{t}=V2,即 v ∈ V 1 v\in V_{1} v∈V1,符合闭合图的定义。
所以只要存在简单割,就必存在闭合图,反之亦然。
因为最小割是简单割,所以当取最小割时,也会存在闭合图。
(若把源点连的边简称为源边,汇点连的边为汇边,点也同理)
此时闭合图的点权和应为S所经的所有原图上的点的点权和,也就是最小割经过某条源边时,意味着不选中那条边不为源点的端点(S无法流经),经过某条汇边时,意味着选中那条边不为汇点的端点(说明汇边无法通过),即该端点 ∉ T \notin T ∈/T,即 ∈ S \in S ∈S。
因为那些汇点原本权值为负,而这里转化成汇边的权值取了绝对值。
也就是闭合图为 S u m 割 未 经 过 的 源 边 − S u m 割 经 过 的 汇 边 Sum_{割未经过的源边}-Sum_{割经过的汇边} Sum割未经过的源边−Sum割经过的汇边
那么设割经过的源边的边权和为 x \mathcal x x,经过的汇边的边权和为 y \mathcal y y,所以割等于(x+y)
则 S u m 割 未 经 过 的 源 边 − S u m 割 经 过 的 汇 边 = ∑ u ∈ V + − ( x + y ) Sum_{割未经过的源边}-Sum_{割经过的汇边}=\sum_{u\in V+}-(x+y) Sum割未经过的源边−Sum割经过的汇边=∑u∈V+−(x+y)
也就是闭合图等于所有点权为正的点的点权和减去割的,
所有源边边权和为 S u m x \mathcal Sum_{x} Sumx
则割为 x + y \mathcal x+y x+y,
闭合图为 = S u m x − ( x + y ) \mathcal=Sum_{x}-(x+y) =Sumx−(x+y)
所以割为最小割时即(x+y)取最小值时,闭合图 V 1 V_{1} V1满足点权和最大。
所以我们就可以理解上文这样做的原因了。
最大权闭合图一般适用于一些反应事件发生关系的题目当中,例如一件事情是否发生依赖于其他事情(选课)。
推荐题目:
1、Hdu 3061 Battle
模版题,不多说
2、poj 2987
其实和上一题差不多,只不过要输出在满足利润最大情况下,最少被解雇的人数,此时其实就是求最大权闭合图的点数,从源点DFS,遍历到的点(不包括源点)个数就是答案。
##总结
最小割能应用的范围是无穷无尽的,很多你想不到的题目都能转化成最小割来做。
所以最大流的算法并不难,重点是在把整个题目转化成最小割的模型再用算法解决。希望你们在看完这个blog能够对其有更深刻的理解。
同时,福利来啦!!以上所推荐的题目,都有相应的源码提供给大家参考学习。
源代码
还有相关的论文,里面涉及了很多最小割模型的证明:
资源地址