网络流最大流讲义
学了接近一个半月的网络流,也该做个总结吧。
- 定义
- 网络流与最大流
- 网络流性质
- 最大流算法Dinic
- 概念
- 算法步骤
- BFS
- DFS
- 模拟
- 反向边的存储和查询
- 模版题
定义
网络流与最大流
网络流是指给定一个有向图,和两个点–源点S和汇点T,点之间有连边,
每条边有一个容量限制,可以看作水管,网络流就是指由S点流到T点的一个可行流。
最大流就是指所有可行流里面最大的流。
通俗的讲,就是由若干个运货点,一个是起点,一个是终点,有一些运货点由路相连,每条路有容量限制,走过那条路时运送的货物不能超过其中的容量限制,求最大流就是求从起点运送尽量多的货物到终点,到达终点的货物个数。
网络流性质
同时,网络流也有三个性质:
1、容量限制: f[u,v]<=c[u,v]
2、反对称性:f[u,v] = - f[v,u]
3、流量平衡: 对于不是源点也不是汇点的任意结点,流入该结点的流量和等于流出该结点的流量和。
网络流必须满足这三个性质
第一个很容易理解,就是运送的货物不能够超出限制
第二个也很容易理解,v向u流入x,v减少,u增加,如果从反方向看,就意味着
u减少-x,v增加-x,也就是u向v流入-x
第三个就是除了源点和汇点的运货点不能够囤货,收到货物就要发出去。
最大流算法Dinic
最大流的算法有很多,有EK,Dinic,ISAP等
现在就介绍一种时间效率很高的算法–Dinic,
概念
其实EK,Dinic都有一个统一的思路–找增广路,
相信同学们在学二分图的时候已经听过这个名词,
增广路的意思是在当前网络之后找到一条能够从源点到汇点能运更多货物的路径。当一条边被增广之后(即它是增广路的一部分,或者说增广路通过这条边),这条边还能通过的流量,叫做剩余流量,修改之后的图称为残量网络。
所以这类算法的思路就是,一直找增广路,找到没有为止
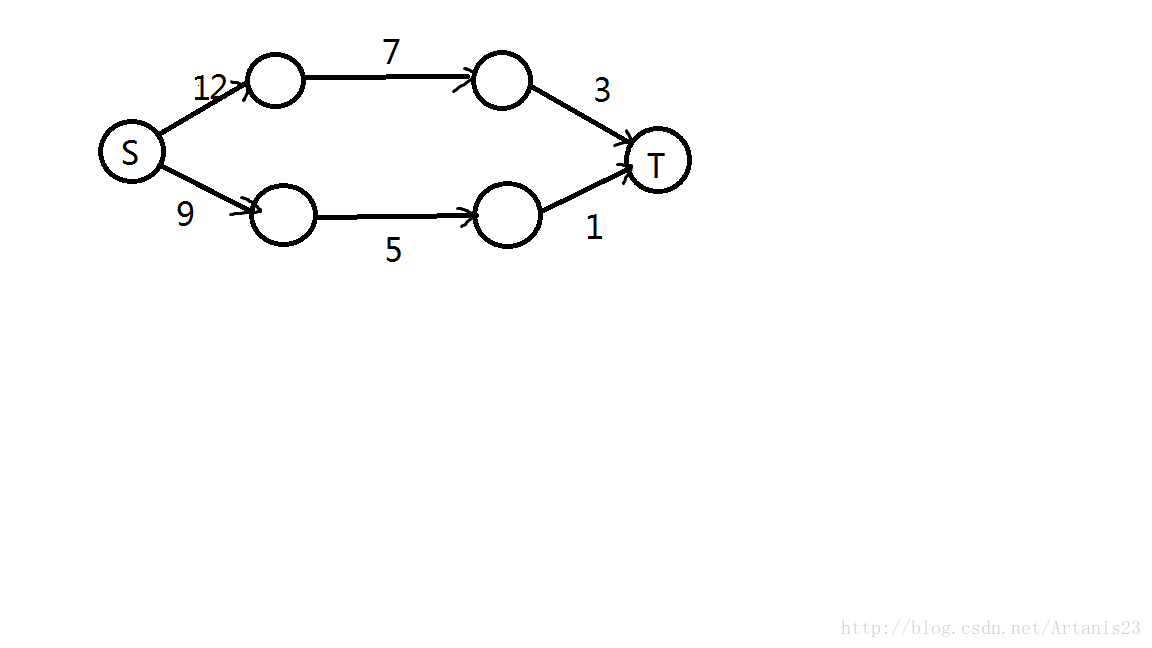
但是如果走完增广路,有更优的流法怎么办?例如说:
又图可知,最大流为4,
但在这个图里面,若算法选择了红色路径为增广路,
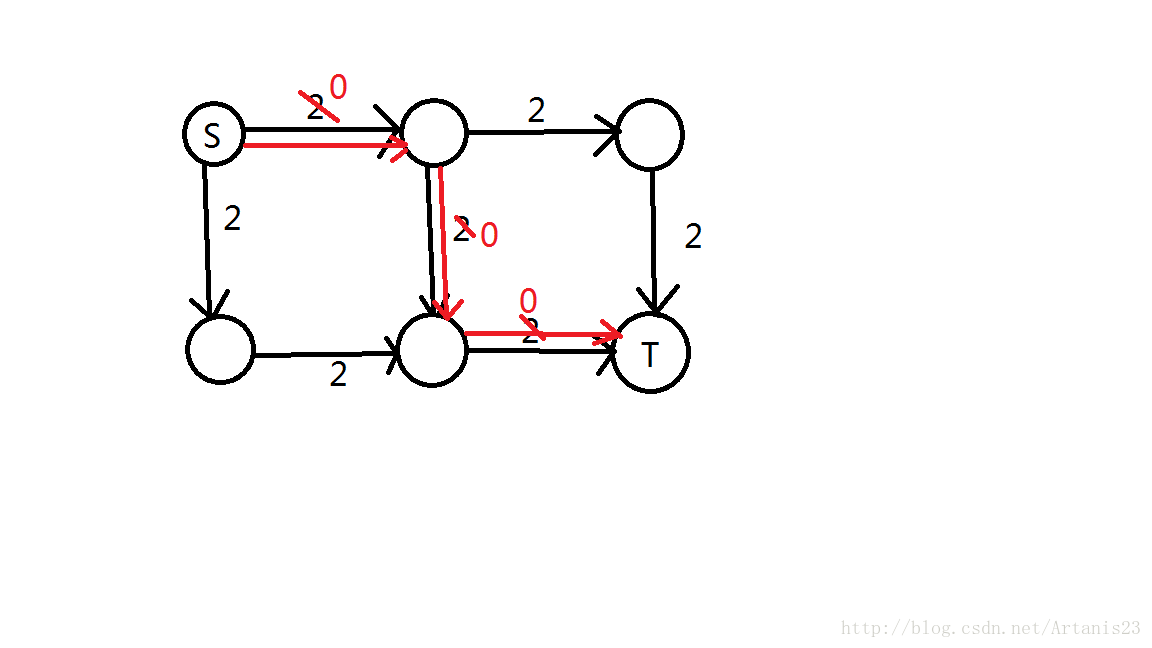
此时流为2,这样走之后就找不到增广路了,因此最大流为2,显然不对。
所以我们不能够单纯的寻找,需要给程序提供一个反悔的机会,
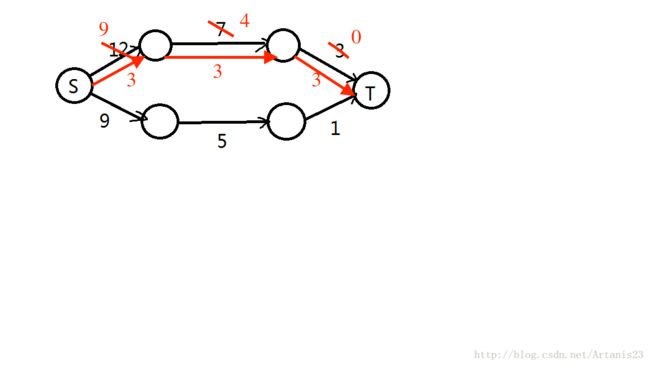
在这里我们引入一个反向弧的概念,也就是在增广的同时,给增广路上的边的反向边容量增加所增广流量:

意思是,程序可以反悔,把所流的流量流回去。
按照这个步骤,继续执行下去,程序就会找到另一条增广路,从而得到正确答案。
将原本红色的增广流量流回去到1点,然后换一条路径到-2-T,此时蓝色就可以走4-T增广,其实是一种“偷梁换柱”的手法。
引入反向弧后,就能解决这个问题。
算法步骤
Dinic算法是在找增广路 前提下加了几个优化,
先给一个步骤,后面详细解释:
1.用BFS建立分层图
2.用DFS的方法寻找一条由源点到汇点的路径,获得这条路径的流量x.
根据这条路径修改整个图,将所经之处正向边流量减少x,反向边流量增加x
重复步骤2,直到DFS找不到新的路径时,重复步骤1
1、BFS
为了避免走重复的路径,
首先从S点BFS,将整个图分成若干层,变成层次图,S点为第0层,
定义dis[u]为u所在的层数,也就是至源点的最短距离。
(tips:如果u点到下一个节点v的边剩余容量为0,则算法忽略此边,因为剩余容量为0已经无法增广)
例如说:
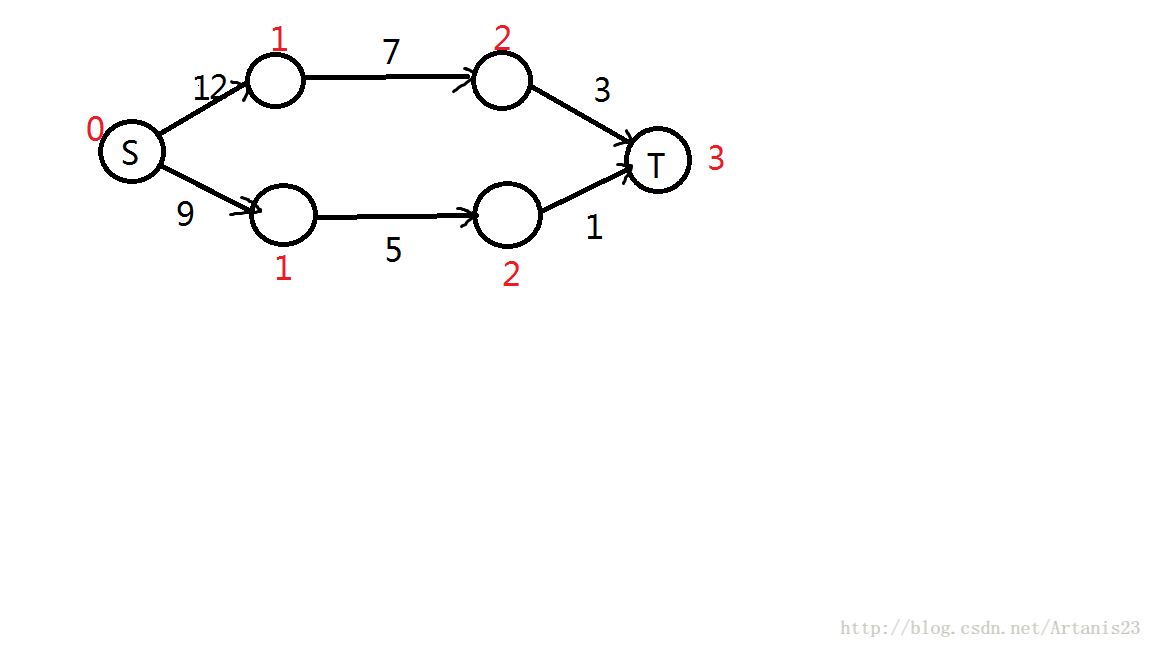
如果在BFS的时候没有遍历过T点,则说明源点与汇点不连通,函数返回0,算法结束。
有的话,返回1,代表建立成功,那么dis数组可以为接下来的DFS寻找增广路提供优化。
2、DFS
在BFS之后就要从源点开始DFS找增广路,
DFS(u,exp)表示经过u点时当前流量为exp。
刚开始时从源点DFS时,exp=∞,表示从该点流出的流量可以为无限大。
在DFS中遍历u所连接的点v,dis[v]必须等于dis[u]+1,否则会多走没有必要的路径。
可以利用DFS进行多路增广来保证时间效率,即一次增广多条路。
因边有流量限制,所以DFS(u,exp) =∑u的节点vDFS(v,min(exp,当前边剩余流量)
当u点为T时,就等于找到一条由S点到T点的增广路,返回exp至上一层。
当u点不为T时,定义一个值flow为在u点所增广的流量,初始值为0
同时要找下一个节点以DFS(节点是一条以u为起点的边上的终点),
但需要一些限制,首先dis[v]=dis[u]+1,而且该边的剩余容量不能为0,否则肯定不能够增广更多的流量。
对于每次节点的DFS,如果该DFS可以增广的流量为0,说明增广失败,就直接跳过后面,找下一个节点v。
不为0的话,当前exp就减去增广路的流量,代表着在u点还可以流的流量,如果exp已经等于0就代表着在该点已经没有更多流量可以流过去了,必须退出增广。
flow加上该增广路增广流量。
同时,正向边减去流量,代表剩余流量,反向边加上流量(反向弧)
最后,该点所有的节点遍历完后,返回该点所增广的流量flow给上一层。
整个DFS结束后,最大流累加器ans加上S点的增广流量,因为停止了DFS,
所以已经没有路可以增广,所以重新BFS给当前残余网络建层次图。
如果BFS返回0,即S点和T点不联通时,直接退出,输出当前ans,
也就是最大流
即伪代码:
while(BFS()):
ans += DFS(S,inf)这样,Dinic算法的步骤就结束了。
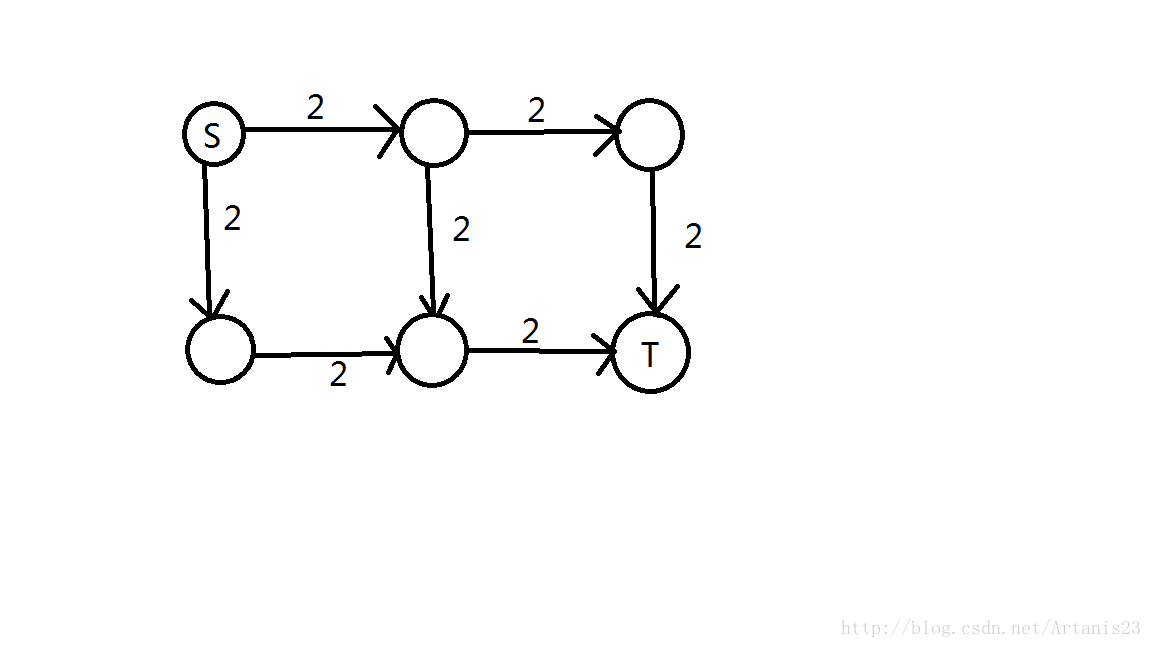
模拟
首先用BFS分层,层次图如下:

分层后开始由S点DFS,
首先DFS(S,∞):
找到下一个节点3,dis[3]=dis[S]+1,所以可以,
此时流进3的最大流量只能是现在走过路径所允许的容量和当前点点流量的最小值,即min(∞,5)=5,即进入DFS(3,5)。
DFS(3,5):
找到下一个节点T,此时流进T最大流量为min(5,3)=3。
所以进入DFS(T,3)
DFS(T,3):
因为走到T,所以找到一条增广路,流量为3,返回增广流量3上一层。
DFS(3,5):
找到一条增广路,所以当前点3还可以流的流量为:5-3=2(留了一些到T点),在该点所增广得到的流量为0+3=3
正向边减3,反向弧加3,也就是:

然后从3寻找下一个节点1,由于dis[1]!=dis[3]+1,所以跳过。
接下来没有其他节点了,返回该点所增广流量3到上一层。
DFS(S,∞):
在节点3得到增广流量3,所以当前节点可流流量,∞-3=∞(S点可流无穷的水),在S点增广得到的流量为:0+3=3
同理,正向边减3,反向弧加3,也就是:

修改完边之后,遍历S下一个节点1,因为dis[1]=dis[S]+1,所以没有问题,能流进1最大流量:min(∞,5)=5,所以进入DFS(1,5)
DFS(1,5):
找到下一个节点2,dis[2]=dis[1]+1,
能流进2最大流量:min(5,6)=5,所以DFS(2,5)
DFS(2,5):
找到下一个节点T,dis[T]=dis[2]+1,
能流进T最大流量:min(5,10)=5,所以DFS(T,5)
DFS(T,5):
走到T了,直接返回增广流量5给上一层。
DFS(2,5):
flow=0+5=5,该点还可以流的流量为5-5=0,
正向边减5,反向边加5,也就是:
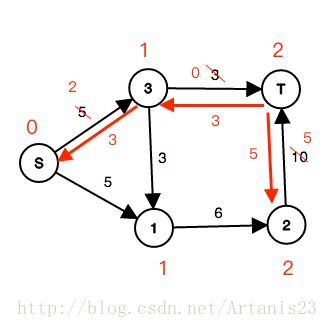
返回5到上一层
DFS(1,5):
flow=0+5=5,还可流流量5-5=0,正向边减5,反向边加5,
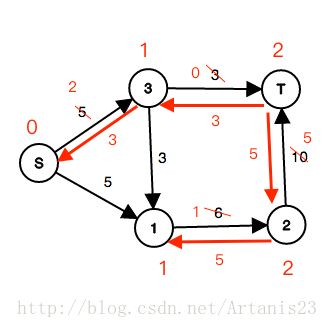
返回5到上一层
DFS(S,∞):
flow=5+3=8,还可流流量∞,正向边减5,反向边加5,
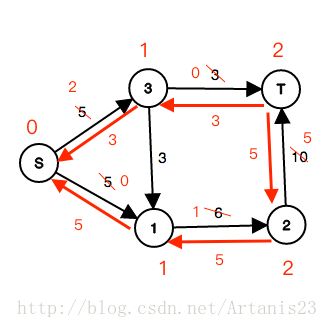
因为是源点,且此时已经找不到下一个节点,所以不用回溯,累加器ans加上8。
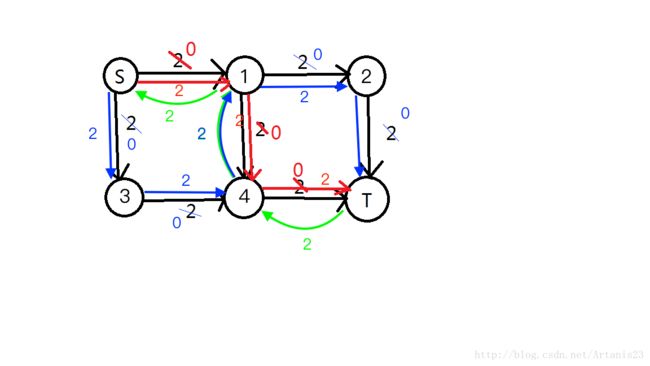
因为找不到下一条增广路,所以重新BFS分层,分层后如图所示:
(剩余容量为0的边忽略,因为其不能通过任何流量)
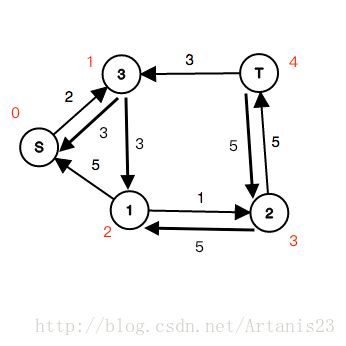
到这里请某位模拟大神上来模拟一下。
模拟后,你们对算法的过程应该会有更深刻的了解。
反向边的存储和查询
那么,在实际编程中,有什么要注意的?
首先,网络流的边可以用链式前向星存储,你们应该知道,就是:
struct Edge{
int v,w,nxt;
}g[MAXM];
int head[MAXN],cnt;
void addEdge(int u,int v,int w){
g[cnt]=(Edge){v,w,head[u]};
head[u]=cnt;
++cnt;
}然而反向弧应该怎么存储呢,在dfs过程中addEdge新建边显然是不现实的,
所以可以在建图过程中加了普通边后,把反向边addEdge,容量为0,这样会方便加。
例如:
addEdge(u,v,w);addEdge(v,u,0);那么如何求一条边的反向边呢,假设那条边的编号为i,那么反向边应为i^1,
例如说u-v编号为3,其反向边v-u编号为3^1=2,
v-u编号为2,其反向边u-v编号为2^1=3。
但要注意的是边的编号要从0开始,否则这种方法无效
模版题
只要理解之后,最大流其实很简单,其实还有很多的优化,
在这里就由于时间关系不讲了,可以课后找我问。
同时也给你们推荐一道模版题 「网络流模板」图图的最大流
可以拿来测你们模版的时间(打满优化才能A)
在这里贴出另一道数据水的模版题poj1273代码(不加优化的,要加满优化的找我):
#include