数据结构基础15：二叉树的前序、中序和后序遍历
前言：到目前为止，我们已经介绍了线性数据结构和表数据机构（哈希表）。这些数据机构一般都不适合表示具有层级结构的数据。在层次化的元素之间有祖先—后代、上级—下属、整体—部分以及其他类似的关系。
一、树的介绍
1、树的定义：
树状图是一种数据结构，它是由n（n>=0）个结点组成一个具有层次关系的有穷集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。n=0的树是空树。
在任意一棵非空树中：
- 有穷集中的每一个元素称为结点。
- 有一个特定的结点被称为根结点或树根（root），根节点在顶部。
- 当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1，T2，..., Tm，其中每个结点Ti本身也是一棵树，被称作根节点的子树（subtree）。
故树也可以这样定义：树是由根结点和若干颗子树构成的。
2、树的相关术语
设T1,T2,..,Tk是树，它们的根结点分别为n1,n2,..,nk。用一个新结点n作为n1,n2,..,nk的父亲，则得到一棵新树，结点n就是新树的根。我们称n1,n2,..,nk为一组兄弟结点，它们都是结点n的子结点。我们还称T1,T2,..,Tk为结点n的子树。
- 父节点（Parent）：若一个节点含有子节点，则这个节点称为其子节点的父节点；
- 子节点（Child）：一个节点含有的子树的根节点称为该节点的子节点；
- 兄弟节点：具有相同父节点的节点互称为兄弟节点；
- 叶子:在树中没有孩子的结点
- 节点的度：其子节点的个数
- 树的度：一棵树中，最大的节点的度称为树的度
- 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推
- 树的高/深度：树中节点的最大层次
- 节点的祖先：从根到该节点所经分支上的所有节点；
- 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
- 森林：由m（m>=0）棵互不相交的树的集合称为森林；
二、二叉树的介绍
1、二叉树的定义和特性
定义：每个节点最多含有两个子树的树称为二叉树。通常子树被称作左子树和右子树。
递归定义：二叉树是n(n>=0)个有限结点构成的集合。N=0称为空二叉树；n>0的二叉树由一个根结点和两互不相交的，分别称为左子树和右子树的二叉树构成。
二叉树常被用于实现二叉查找树和二叉堆。二叉树是一个连通的无环图，并且每一个顶点的度不大于3。
数与二叉树的区别：
二叉树的每个元素都恰好有两颗子树（其中或两个可能为空）。而树的每个元素可有任意数量的子树。
二叉树中，每个元素的子树都是有序的，也就是说，有左子树和右子树之分。而树的子树是无序的。
特性：
- 一颗二叉树有n(n>0)个元素，它有n-1条边；
- 一颗二叉树有n(n>0)个元素，它的最小高度为
（注：[ ]表示向下取整） - 一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1；
- 深度为h的二叉树最多有
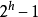个结点(h>=1)，最少有h个结点；
满二叉树：当高度为h的二叉树恰好有 个元素时，称其为满二叉树（full binary tree）。
所有的分支结点都存在左子树和右子树，并且所有的叶子结点都在同一层上，这样就是满二叉树。就是完美圆满的意思，关键在于树的平衡。
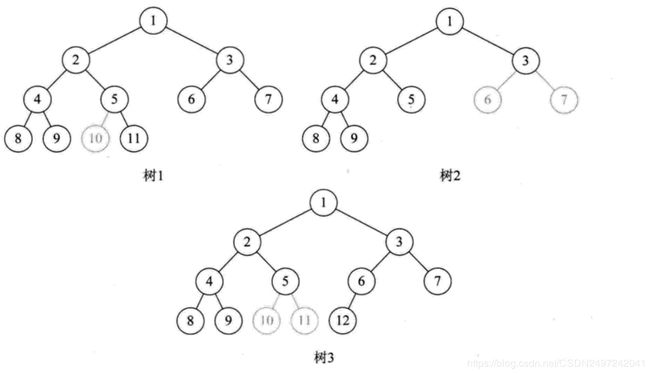
完全二叉树：完全二叉树是效率很高的数据结构，若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。
完全二叉树是由满二叉树而引出来的。对于深度为h的，有n个结点的二叉树，当且仅当其每一个结点都与深度为h的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树（如果编号为i的结点与同样深度的满二叉树编号为i结点在二叉树中位置完全相同）。满二叉树必须是完全二叉树，反过来不一定成立。
具有n的结点的完全二叉树的深度为[log2n]+1。
斜树：所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。
2、二叉树的描述
数组存储方式：把二叉树看做是缺少了部分元素的完全二叉树，所有元素依旧按照层序从左至右编号。那么在数组表示中，二叉树按照其编号存储在数组的相应位置。
当缺少的元素很多时，这种表示方法很浪费空间，一个有n个元素的二叉树可能最多需要2的n次方个空间来存储。
故只有当缺少元素较少时，这种描述方法才有用，顺序存储一般适用于完全二叉树。
链表存储方式：
既然顺序存储不能满足二叉树的存储需求，那么考虑采用链式存储
每个元素用一个节点表示，节点有两个指针域，分别称为leftChild和rightChid，除了两个指针域外，每个节点还有一个data域。
/*
* 链表二叉树的节点结构
*/
public class BinaryTreeNode
{
T data;
BinaryTreeNode leftChild;//左子树
BinaryTreeNode rightChild;//右子树
public BinaryTreeNode(){};
public BinaryTreeNode(final T data)
{
this.data = data;
}
public BinaryTreeNode(final T data,BinaryTreeNode leftChild, BinaryTreeNode rightChild)
{
this.data = data;
this.leftChild= leftChild;
this.rightChild = rightChild;
}
}
3、二叉树的遍历
二叉树是一种递归定义的数据结构，所以用递归来写它的相关算法是顺理成章的。
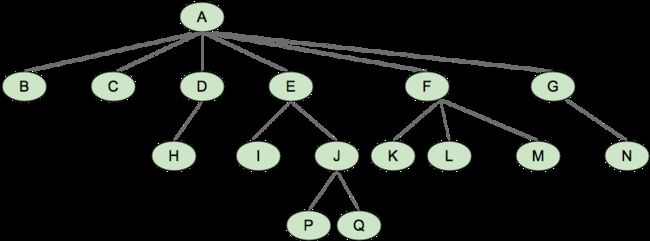
图4-1
①二叉树的前序遍历：先访问一个节点，再访问该节点的左右子树。
前序遍历输出为：ABDHIEJCFG
②二叉树的中序遍历：先访问一个节点的左子树，然后访问该节点，最后访问右子树。
中序遍历输出为：HDIBJEAFCG
③二叉树的后序遍历：先访问一个节点的左右子树，再访问该节点。
后序遍历输出为：HIDJEBFGCA
④二叉树的层次遍历
层次遍历就是按照树的层次自上而下的遍历二叉树。针对图4-1所示二叉树的层次遍历结果为：ABCDEFGHIJ
二叉树的递归遍历过程：彻底理解递归，从递归的本质说起！
递归实现的Java代码：
public class BinaryTreeScan
{
//访问节点node，仅输出data域
public void visit(BinaryTreeNode node)
{
System.out.println(node.data);
}
//前序遍历二叉树root
public void preOrder(BinaryTreeNode root)
{
if(root!=null)
{
visit(root);//访问树根
preOrder(root.leftChild);//前序遍历左子树
preOrder(root.rightChild);//前序遍历右子树
}
else
System.out.println("Binary tree is empty!");
}
//中序遍历二叉树root
public void inOrder(BinaryTreeNode root)
{
if(root!=null)
{
inpOrder(root.leftChild);
visit(root);
inOrder(root.rightChild);
}
else
System.out.println("Binary tree is empty!");
}
//后序遍历二叉树root
public void postOrder(BinaryTreeNode root)
{
if(root!=null)
{
preOrder(root.leftChild);
preOrder(root.rightChild);
visit(root);
}
else
System.out.println("Binary tree is empty!");
}
//层次遍历
public void levelRead(BinaryTreeNode root)
{
if(root == null)
return;
Queue> queue = new LinkedList>() ;
while(root!=null)
{
visit(root);
//将root的孩子插入队列
if(root.leftChild!=null)
queue.offet(root.leftChild);
if(root.rightChild!=null)
queue.offer(root.rightChild)
//提取下一个要访问的节点
root = queue.peek();
queue.poll();
}
} 4、确定二叉树的高度
1、递归求解的方法，其实属于DFS深度优先搜索算法。
public int getHeight(BinaryTreeNode root)
{
if(root == null)
{
return 0;
}
int i = getHeight(root.left);//左树高
int j = getHeight(root.right);//右树高
return (i 2、层次遍历的方法，属于BFS广度优先搜索算法。
其实还有非递归实现：层次遍历，使用队列。每往下遍历一层，树的高度增加1；当遍历结束，自然可以得到树的高度；
int TreeDepth(TreeNode* pRoot)
{
if(pRoot == NULL){
return 0;
}
queue que;
int depth = 0;
que.push(pRoot);
while(!que.empty()){
int size = que.size();
depth++;
for(int i = 0; i < size; i++){
TreeNode* node = que.front();
que.pop();
if(node->left){
que.push(node->left);
}
if(node->right){
que.push(node->right);
}
}
}
return depth;
} 三、二叉树遍历的两个典型题型，每年考研的必考题。
1）已知前序遍历序列和中序遍历序列，确定一棵二叉树。
例题：若一棵二叉树的前序遍历为ABCDEF，中序遍历为CBAEDF，请画出这棵二叉树。
分析：前序遍历第一个输出结点为根结点，故A为根结点。早中序遍历中根结点处于左右子树结点中间，故结点A的左子树中结点有CB，右子树中结点有EDF。
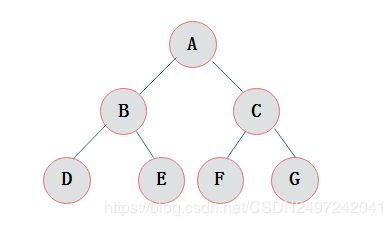
如图3-1所示：
图3-1
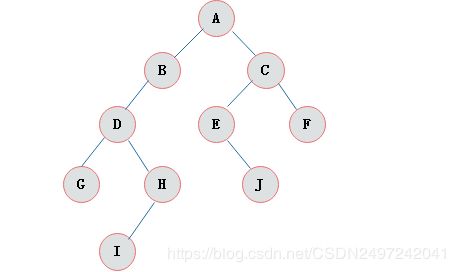
按照同样的分析方法，对A的左右子树进行划分，最后得出二叉树的形态如图3-2所示：
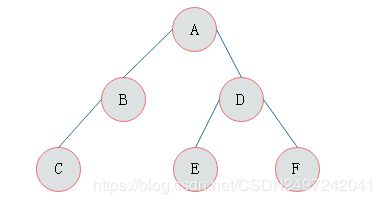图3-2
2）已知后序遍历序列和中序遍历序列，确定一棵二叉树。(LeetCode上相关题目)
后序遍历中最后访问的为根结点，因此可以按照上述同样的方法，找到根结点后分成两棵子树，进而继续找到子树的根结点，一步步确定二叉树的形态。
注：已知前序遍历序列和后序遍历序列，不可以唯一确定一棵二叉树。
代码：已知一颗二叉树的后序遍历序列和中序遍历序列，写出可以确定这颗二叉树的算法
参考链接：深入学习二叉树(一) 二叉树基础