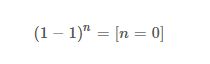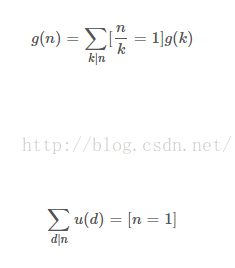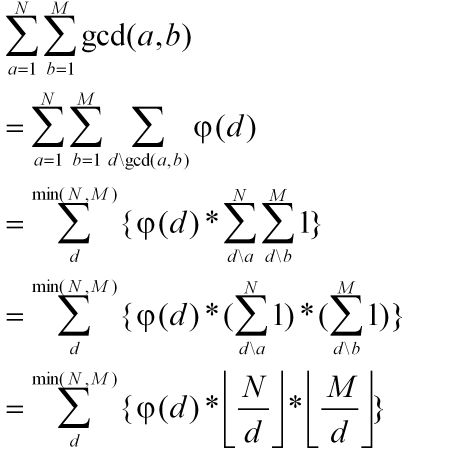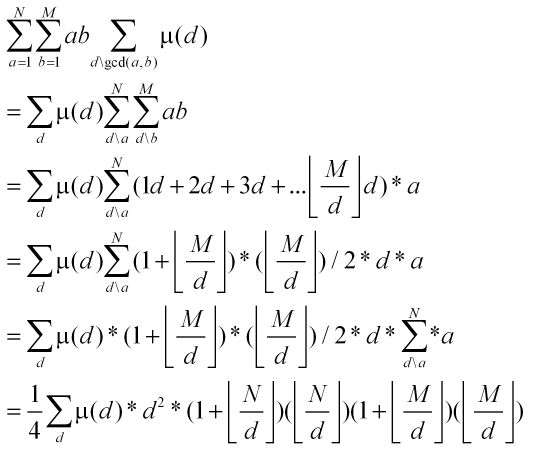浅谈变换(证明)→反演→莫比乌斯反演→线筛运用
首先我们先引入基础错排,借用比较有趣的说法↓:
那么为何引入这个?
这个错排的计算方式与普通方式不一样,也是为了后面证明反演做铺垫。
那我们先看一下错排的一般计算推导式:
n 个不同元素的一个错排可由下述两个步骤完成:
第一步,“错排” 1 号元素(将 1 号元素排在第 2 至第 n 个位置之一),有 n - 1 种方法。
第二步,“错排”其余 n - 1 个元素,按如下顺序进行。视第一步的结果,若1号元素落在第 k 个位置,第二步就先把 k 号元素“错排”好, k 号元素的不同排法将导致两类不同的情况发生:
1、 k 号元素排在第1个位置,留下的 n - 2 个元素在与它们的编号集相等的位置集上“错排”,有 f(n -2) 种方法;
2、 k 号元素不排第 1 个位置,这时可将第 1 个位置“看成”第 k 个位置(也就是说本来准备放到k位置为元素,可以放到1位置中),于是形成(包括 k 号元素在内的) n - 1 个元素的“错排”,有 f(n - 1) 种方法。据加法原理,完成第二步共有 f(n - 2)+f(n - 1) 种方法。
根据乘法原理, n 个不同元素的错排种数
f(n) = (n-1)[f(n-2)+f(n-1)] (n>2) 。
(至于级数得到的那个推导式,有兴趣可以自己证一下)
接下来,引入3个很普通的公式:
然后结合,可以得到:
这样,我们便得到了普通的二项式反演:
莫比乌斯反演呢?可以借助上述的形式“简单推”:首先,下面左边两条式子和上面那三个普通的公式有关联,那就是都很普通,然后可以类推出右边的公式:
上面都是在讲莫比乌斯反演的推导→为了方便记忆,并没有比较详细地介绍莫比乌斯反演公式的具体内容,
可以参考这篇博文自行了解:http://www.cnblogs.com/Milkor/p/4464515.html
怎么求莫比乌斯反演?
强行筛u
这是种暴力的方法(不是原创的代码)
筛莫比乌斯函数的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
void mobius() { memset(check, false, sizeof(check)); mu[1] = 1; int tot = 0; for (int i = 2; i <= N; i++) { if (check[i]) { prime[++tot] = i; mu[i] = -1; } for (int j = 1; j <= tot; j++) { if (i * prime[j] > N) break; check[i * prime[j]] = true; if (i % prime[j] == 0) { mu[i * prime[j]] = 0; break; } else mu[i * prime[j]] = -mu[i]; } } } |
1:给T组N,M.依次求出 的值.(N,M<=10^6,T<=10^3)
的值.(N,M<=10^6,T<=10^3)
求解gcd(a,b).把gcd(a,b)当做n.再通过欧拉函数和式。推导过程如下。
第二个等式是用d来看待式子的方法来化简和式的。
之后再穷举d即可。
代码:#include
#include
#define N 100
bool mark[N+5];
int prime[N+5];
int num;
int euler[N+5];
int Min(int a,int b){return a>b?a:b;}
void Euler()
{
int i,j;
num = 0;
memset(euler,0,sizeof(euler));
memset(prime,0,sizeof(prime));
memset(mark,0,sizeof(mark));
euler[1] = 1; // multiply function
for(i=2;i<=N;i++)
{
if(!mark[i])
{
prime[num++] = i;
euler[i] = i-1;
}
for(j=0;jN){break;}
mark[i*prime[j]] = 1;
if(i%prime[j]==0)
{
euler[i*prime[j]] = euler[i]*prime[j];
break;
}
else
{
euler[i*prime[j]] = euler[prime[j]]*euler[i];
}
}
}
}
int main()
{
int i;
int M1,M2;
Euler();
for(i=0;i 2.给T组N,M.依次求出 的值.(N,M<=10^6,T<=10^3)
的值.(N,M<=10^6,T<=10^3)
在证明之前,先证明以下式子。
问题的解决推导。
第一个等式。lcm(a,b) = ab/gcd(a,b).
第二个等式。令d=gcd(a,b)。
第三个等式。转化为d的视角。(这个手法经常有)。
第四个等式。转化为莫比乌斯函数。
第五个等式。利用上述的等式来转化。注意d和d'
第六个等式。论文中提到的有趣的化简性质。
第七个等式。其实是d = dd'换元。不过有点老奸巨猾啊。干嘛不设个T = dd'。这个我纠结了半天。
之后就是如论文中介绍的。g(d) 为积性函数。线性筛之。
总体上算法还是N的。
(线筛并没有很详细地讲,之后会有更新,上述内容有参考其它文章)