There's a beach in the first quadrant. And from time to time, there are sea waves. A wave ( xx , yy ) means the wave is a rectangle whose vertexes are ( 00 , 00 ), ( xx , 00 ), ( 00 , yy ), ( xx , yy ). Every time the wave will wash out the trace of former wave in its range and remain its own trace of ( xx , 00 ) -> ( xx , yy ) and ( 00 , yy ) -> ( xx , yy ). Now the toad on the coast wants to know the total length of trace on the coast after n waves. It's guaranteed that a wave will not cover the other completely.
Input
The first line is the number of waves n(n \le 50000)n(n≤50000).
The next nn lines,each contains two numbers xx yy ,( 0 < x0
Output
An Integer stands for the answer.
Hint:
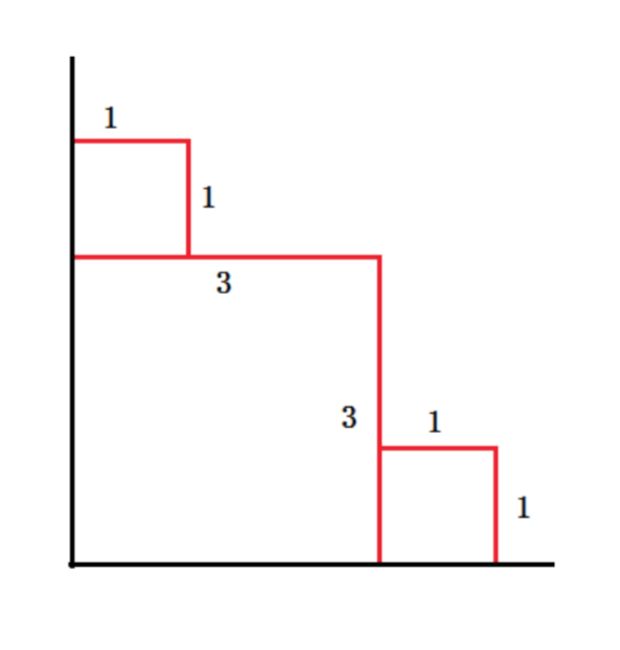
As for the sample input, the answer is 3+3+1+1+1+1=103+3+1+1+1+1=10
样例输入复制
3
1 4
4 1
3 3
样例输出复制
10
题目来源
ACM-ICPC 2018 徐州赛区网络预赛
思路:对于每个矩阵按照输入顺序分析,先分析矩阵 i 的长xi,求出它被覆盖的长度,即求出 大于矩阵i的高yi的矩阵的长的最大值MaxX,在判断MaxX与xi的大小, MaxX
Code :
#include
#include
#include
#include
#include
