【代码】数据结构与算法

快速排序

def quick_sort(alist, first, last):
    if first>=last:
        return
    mid = alist[first]
    low = first
    high = last
    while low=mid:
            high-=1
        alist[low]=alist[high]
        while low

冒泡排序

def bubble_sort(a):
    for i in range(len(a)):
        flag = False
        for j in range(len(a) - i - 1):
            if a[j] > a[j + 1]:
                a[j], a[j + 1] = a[j + 1], a[j]
                flag = True
        if flag is False:
            break
    return a

插入排序

def insert_sort(a):
	if len(a)<2:
		return
	for i in range(0,len(a)):
		value = a[i]
		j = i -1
		while j>=0:
			print(j)
			if a[j]>value:
				a[j+1] = a[j]
			else:
				break
			j -= 1
		# for不能排序第一个元素，不知道为什么
		# for j in range(i-1,-1,-1):
		# 	print(j)
		# 	if a[j]>value:
		# 		a[j+1] = a[j]
		# 	else:
		# 		break
		a[j+1] = value

冒泡排序的数据交换要比插入排序的数据移动要复杂，冒泡排序需要 3 个赋值操作，而插入排序只需要 1 个。插入排序优化空间也很大。
要注意在插入排序遍历时，不要进行元素交换（3个赋值操作），只需在往前遍历的过程中，同时后移一次元素（1个赋值操作），否则会降低性能

计数排序
适用于一定范围内的整数，比快排更快
不稳定版：

def count_sort(ls):
    # 对数组长度进行优化, 初置0,
    minls = min(ls)
    maxls = max(ls)
    ls2 = [0] * (maxls-minls+1)
    # 进行计数
    for i in ls:
        ls2[i-minls] += 1
    print(ls2)
    # 从索引拿出数
    ls3 = []
    for i in range(len(ls2)):
        ls3 += [i+minls] * ls2[i]
    return ls3

稳定版：…

红黑树
应用于TreeMap，TreeSet 和 java8 的 Hashmap 当中。
红黑树是特殊的平衡二叉树。
自平衡是插入和删除后处理。自平衡确实会占一定的时间，但是让读操作的时间大大减少，适用于读多写少的场景。

Hashmap
数组默认初始长度16。因为长度必须是2的幂，Hash算法通过HashCode和Length-1的&运算得到index，其实结果也就是HashCode的后几位值。所以只要HashCode是均匀的，Hash算法就是均匀分布。
数组元素是链表，只有头节点。java8当中，链表长度超过8的时候会变成红黑树。
HashSet在内部封装了一个Hashmap对象。

B-树
MongoDB，在索引树的节点内部中有很多元素，因此减少磁盘IO，增加在内存中的比较，以提高查找速度。卫星数据和关键字都在节点中。

B+树
Mysql，索引树的单一节点存储更多元素，IO次数更少。
卫星数据都存在叶子结点，查询性能稳定，中间节点不保存数据。
所有叶子节点形成有序链表，便于范围查询。

树的遍历
根结点所处位置: 中序遍历根放在最中间, 前序根放在第一个, 后序根放在最后一个. 叶结点顺序: 肯定是从左到右的
因此, 对于给出的遍历顺序, 使用前后遍历确定根结点是哪个, 然后从根结点开始, 使用中序遍历切割出叶子, 这样进行递归的判断, 再结合叶子从左到右的顺序, 即可画出树

练一练: 知道中序和后序遍历，画二叉树和写出前序遍历
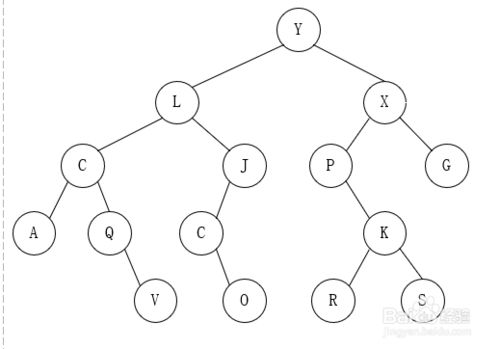
已知中序遍历：ACQVLCOJYPRKSXG
后序遍历：AVQCOCJLRSKPGXY
画出二叉树，前序遍历是YLCAQVJCOXPKRSG

二分查找

def binary_search(ls, k):
    ls.sort()  # 如果没有排序, 必须先排序
    n = len(ls)
    left = 0
    right = n - 1
    while left <= right:
        mid = (left + right) // 2
        if ls[mid] > k:
            right = mid - 1
        elif ls[mid] < k:
            left = mid + 1
        else:
            return True
    return False


print(binary_search([1, 5, 4, 3, 6, 7, 2], 3))


def binary_search2(ls, left, right, k):
    if left > right:
        return False
    mid = (left + right) // 2
    if ls[mid] > k:
        return binary_search2(ls, left, mid - 1, k)
    elif ls[mid] < k:
        return binary_search2(ls, mid + 1, right, k)
    else:
        return True


ls = [1, 5, 4, 3, 6, 7, 2]
ls.sort()
print(binary_search2(ls, 0, len(ls) - 1, 2))