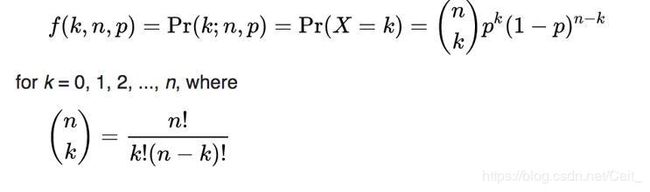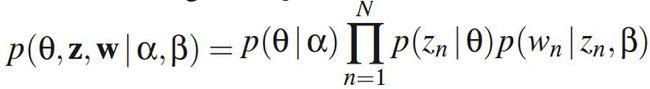数据挖掘(一)主题模型(Topic Modeling)
数据挖掘(一)主题模型(Topic Modeling)
1. 主题建模的目的
从文档集合中自动地找出一系列的主题(topics),每个文档集内可能有多个主题;
主题:由众多词汇的概率分布(distribution)组成;
常用模型:LDA, pLSA, pLSI等,是一种无监督的学习过程;
Input: An unorganized collection of documents;
Output: An organized collection of topics;
在生活中,完成文档的过程是:首先确定这篇文章的中心思想(topic),然后根据topics,产生一个个词语(words),最终形成文档。主题模型的过程与之相反,通过文档形成词袋,再由词袋生成topic。下图显示的是一个主题模型的简单示例,输入为两个文档,输出为5个topic,每个topic分别由多个词组成;
2. 预备数学知识
2.1 Bernoulli distribution
2.2 Binomial distribution
二项分布:类似于多次抛掷硬币;
2.3 Categorical distribution
分类分布:抛掷一次多面骰子, p 1 + p 2 + p 3 + . . . . . . + p n = 1 p_1+p_2+p_3+......+p_n = 1 p1+p2+p3+......+pn=1

p ( x ) = [ x = 1 ] p 1 + [ x = 2 ] p 2 + [ x = 3 ] p 3 + . . . . . . + [ x = 6 ] p 6 p(x)=[x=1]p_1+[x=2]p_2+[x=3]p_3+......+[x=6]p_6 p(x)=[x=1]p1+[x=2]p2+[x=3]p3+......+[x=6]p6
[ x = 1 ] [x=1] [x=1]表示艾弗森括号,如果方括号内的条件满足则为1,不满足则为0;
2.4 Multinomial distribution
多项式分布, x i x_i xi代表 X i X_i Xif发生的次数, ∑ x i = 1 \sum x_i = 1 ∑xi=1, p i p_i pi代表 X i X_i Xi事件发生的概率;
2.5 Gibbs Sampling
吉布斯采样(Gibbs sampling)是统计学中用于马尔科夫蒙特卡洛(MCMC)的一种算法,用于在难以直接采样时从某一多变量概率分布中近似抽取样本序列,它假定每一条序列只包含一个特定长度的模体实例,在各条序列上随机选取一个模体的起始位置,这样便得到了初始训练集,然后通过更新步骤和采样步骤迭代改进模体模型。
假定我们要从 p ( x 1 , . . . . . . , x n ) p(x_1, ......, x_n) p(x1,......,xn)中抽取 X = ( x 1 , . . . . . . , x n ) X=(x_1, ......, x_n) X=(x1,......,xn),对于 X i + 1 X^{i+1} Xi+1中的每个分量 X j i + 1 X^{i+1}_j Xji+1,由 X i = ( x 1 i , x 2 i , . . . . . . , x n i ) X^i=(x^i_1,x^i_2,......,x_n^i) Xi=(x1i,x2i,......,xni)和已经计算出的 X i + 1 = ( x 1 i + 1 , . . . . . . , x j − 1 i + 1 ) X^{i+1}=(x^{i+1}_1,......,x^{i+1}_{j-1}) Xi+1=(x1i+1,......,xj−1i+1)联合计算,即:
p ( x j i + 1 ∣ x 1 i + 1 , . . . . . . , x j − 1 i + 1 , x j i , . . . . . . , x j n ) p(x^{i+1}_j|x_1^{i+1},......,x_{j-1}^{i+1},x_j^i, ......,x_j^n) p(xji+1∣x1i+1,......,xj−1i+1,xji,......,xjn)
3. LSA(Latent Semantic Analysis)
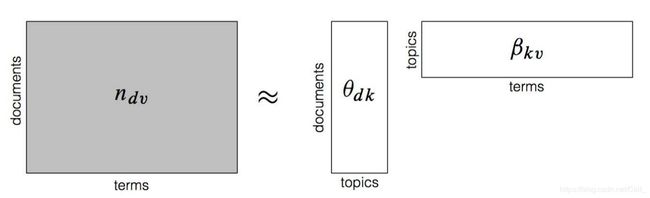
n d v n_{dv} ndv表示文档集词向量分布的矩阵表示,给定topic数量为k,通过奇异值分解,将 n d v n_dv ndv转化为 θ d k β k v \theta_{dk}\beta_{kv} θdkβkv的形式, θ d k [ i ] [ j ] \theta_{dk}[i][j] θdk[i][j]表示第 i i i个文档归纳为第 j j j个topic的概率, β k v [ i ] [ j ] \beta_{kv}[i][j] βkv[i][j]表示第 i i i个topic内出现第 j j j个word的概率;
n d v [ i ] [ j ] n_{dv}[i][j] ndv[i][j]表示在文档 i i i中,出现词 j j j的概率,通常用TF-IDF概率表示,tf表示文档频率,idf表示逆文档频率;
t f i d f ( t , d , D ) = t f ( t , d ) ∗ i d f ( t , d ) tfidf(t,d,D)=tf(t,d)*idf(t,d) tfidf(t,d,D)=tf(t,d)∗idf(t,d)
t f ( t , d ) = ∣ t ∣ ∣ d ∣ tf(t,d) = \frac{|t|}{|d|} tf(t,d)=∣d∣∣t∣
i d f ( t , d ) = l o g N d ∈ D : t ∈ d idf(t,d)=log\frac{N}{ d \in D: t \in d } idf(t,d)=logd∈D:t∈dN
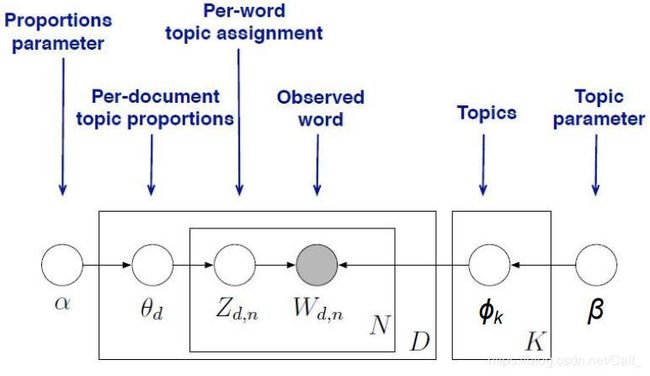
4. LDA(Latent Dirichlet Allocation)
文档集的所有文档共享一组topics,并且每个文档以一定的概率呈现这些topics。
假定文档的生成过程:
STEP 1: 随机地选取topics的概率分布,得到 [ p 1 , p 2 , . . . . . . , p n ] [p_1,p_2,......,p_n] [p1,p2,......,pn];表示在该文档中topic的概率;
STEP 2: 从STEP1中获取的topic分布中采样,得到一个topic;
STEP 3: 再从这个topic对应的词汇表中采样一个word;
STEP 4: 重复STEP 2, STEP 3过程,直到生成整个文档;