【POJ 1191】 棋盘分割(DP)
| Time Limit: 1000MS |
|
Memory Limit: 10000K |
| Total Submissions: 13811 |
|
Accepted: 4917 |
Description
将一个8*8的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了(n-1)次后,连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)
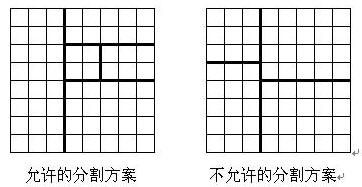
原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差
棋盘分割
| Time Limit: 1000MS |
|
Memory Limit: 10000K |
| Total Submissions: 13811 |
|
Accepted: 4917 |
Description
将一个8*8的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了(n-1)次后,连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差

,其中平均值

,x
i为第i块矩形棋盘的总分。
请编程对给出的棋盘及n,求出O'的最小值。
Input
第1行为一个整数n(1 < n < 15)。
第2行至第9行每行为8个小于100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
Output
仅一个数,为O'(四舍五入精确到小数点后三位)。
Sample Input
3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3
Sample Output
1.633
Source
Noi 99
[Submit] [Go Back] [Status] [Discuss]
 Home Page
Home Page
 Go Back
Go Back  To top
To top

,其中平均值

,x
i为第i块矩形棋盘的总分。
请编程对给出的棋盘及n,求出O'的最小值。
Input
第1行为一个整数n(1 < n < 15)。
第2行至第9行每行为8个小于100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
Output
仅一个数,为O'(四舍五入精确到小数点后三位)。
Sample Input
3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3
Sample Output
1.633
Source
Noi 99
刷了一圈,刷回到最原始的东西。其实也是学不完的东西。。。DP……花样太多了,烧脑特辑。。。
题目很简单粗暴
8*8的一个正方形,每个点有值(0~100)要求切割n-1次,每次只能从余下部分的边出发切割到另一边,题目中的图画的挺清楚的。然后问最小的方差。。。
方差公式是给了。但如果死盯着这公式。。想再久应该也是想不粗来的……
需要变一下形。就借用别的博客的推导了~~
S^2 = 1/n∑(Xi - X)^2
= 1/n(n*X^2 + ∑Xi^2 - 2*X∑Xi)
= 1/n∑Xi^2 - X^2;
(http://blog.csdn.net/xymscau/article/details/6854410)
这样其实应该就有点小想法了~你会发现X(均值)是固定的(sum/n),只要保证∑Xi^2尽可能小,最终的结果就一定是最小值。并且可以发现S^2不会出现负值,也就是说∑Xi^2再小也比X^2要大,因此就可以放心地dp了。或者说,放心地(记忆化)搜索了,每次切割时,继续搜索的部分继续搜,另一部分需要快速给出一个合值,因此可以预处理一下所有的区间的平方,或者每次用到暴力跑也可以。
需要注意的是切出n个矩形要切n-1刀。
还有,dp数组要记得记录切割刀数。。一开始就是因为没记录,导致混乱,最终WA
另外,dp最先初始化的时候不要初始化为INF,因为可能某些部分最终结果就是INF,也就是无解,如果一开始初始化为INF,并且以这为记忆化返回值的判断,会导致超时。因为到此状态时仍会向下dp。正解应为代码中初始化未-1,当发现是第一次搜索该状态时,立马转变为INF,然后搜出该状态最小值(若不合法,恰巧就是上一步赋值的INF(无穷大))
代码如下:
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

