javascript求点的凸集/凸包
最近有一个实际的需求,需要用到求凸集,这次用js实现是为了让自己真正了解此过程,并能检测实现的对不对。
<html>
<head>
<meta charset = "utf-8" / >
<title>TSP_demotitle>
head>
<body>
<div id="outText">
div>
<canvas id="canvas" height="550px" width="1024px">
canvas>
<script type="text/javascript">
var canvas = document.getElementById("canvas");
var canvasWidth = canvas.width;
var canvasHeight = canvas.height;
var context = canvas.getContext("2d");
// 未使用
function initMat(M, N, val) {
var x = new Array();
for(var i = 0; i < M; i++) {
x[i] = new Array();
for(var j = 0; j < N; j++)
x[i].push(val);
}
return x;
}
function drawPath(x1, y1, x2, y2, color, width) {
context.beginPath();
context.fillStyle = color;
context.strokeStyle = color;
context.lineWidth = width;
context.moveTo(x1, y1);
context.lineTo(x2, y2);
context.stroke();
}
function drawCities(p) {
for(var i = 0; i < p.length ; i++) {
context.beginPath();
context.fillStyle = "blue";
context.strokeStyle = "blue";
context.lineWidth = 1;
context.font = "normal 16px Arial";
context.arc(p[i].x, p[i].y, 3, (Math.PI / 180) * 0, (Math.PI / 180) * 360, false);
context.fill();
context.stroke();
context.closePath();
if(p[i].tj==true){
context.fillStyle = "red";
context.textAlign = "center";
context.textBaseline = "middle";
context.fillText(String(i), p[i].x, p[i].y-8);
}
}
}
function output(string){
var out = document.getElementById("outText");
out.innerHTML+=string
}
// 可以借助cos a 在0-180之间,单调递减!!!
// 这里用的是叉积,正弦的判断
function multiply(p0,p1,p2){
return((p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y));
}
function distance_no_sqrt(p1,p2)
{
//return(sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y)));
return((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
function Graham_scan(pointSet,ch,n){
// 这里会修改pointSet
var i,j,k=0,top=2;
var tmp=new Object();
// 找到一个基点,基本就是保证最下面最左面的点
for(i=1;iif ( (pointSet[i].y0];
pointSet[0]=pointSet[k];
pointSet[k]=tmp;
use=n;
for (i=1;i1;i++){
k=i;
for (j=i+1;jvar direct=multiply(pointSet[0],pointSet[k],pointSet[j]);
if(direct>0){
k=j;
}else if(direct==0){
// k j 同方向
var dis=distance_no_sqrt(pointSet[0],pointSet[j])-distance_no_sqrt(pointSet[0],pointSet[k]);
use--; // 也就是不要了
if(dis>0){
// 保留j
// 把 k 就不要了
pointSet[k]=pointSet[j];
pointSet[j]=pointSet[use];
j--;
}else{
tmp=pointSet[use];
pointSet[use]=pointSet[j];
pointSet[j]=tmp;
}
}
}
tmp=pointSet[i];
pointSet[i]=pointSet[k];
pointSet[k]=tmp;
}
ch.push(pointSet[0]);
ch.push(pointSet[1]);
ch.push(pointSet[2]);
for (i=3;iwhile ( !(multiply(pointSet[i],ch[top-1],ch[top]) < 0 ) ){
top--;
ch.pop();
}
top++;
ch.push(pointSet[i]);
}
}
// 求凸集的方法
function Graham_example(){
var n=100; // 用100个例子
var p=new Array(n);
//var res=new Array(n);
var res=new Array();
// 随机初始化定点
for(var i = 0; i < n; i++) {
p[i]=new Object();
p[i].x = (Math.random() * 32767) % 680 + 20;
p[i].y = (Math.random() * 32767) % 320 + 20;
p[i].tj=false
}
drawCities(p)
var t1 = new Date()
t1.setTime(t1.getTime());
Graham_scan(p,res,n)
t2 = new Date();
var ms = t2.getTime() - t1.getTime();
output("
用时(毫秒):
" + ms)
var m=res.length;
res[0].tj=true;
for(var i=1;itrue;
drawPath(res[i-1].x, res[i-1].y, res[i].x, res[i].y, "black", 1);
}
drawPath(res[0].x, res[0].y, res[m-1].x, res[m-1].y, "black", 1);
// canvas 的坐标和我们的不一样
drawCities(res)
}
Graham_example();
script>
body>
html>
运行效果
注意,canvas的原点是在左上角,因此基准点位置看起来与直觉不一样。
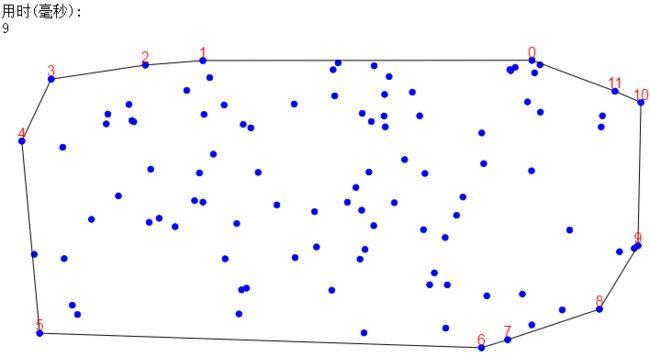
上图中蓝色的点是随机生成的,上面标红色数字的是凸集的顶点。
另外这次用chrome调试,感觉不比firefox差。