数据结构之 AVL平衡树 (c++)

一

     AVL树是一种高度平衡的二叉查找树,这里将会简单的提一下其算法思想,不会讨论复杂度的计算.只是想告诉大家,AVL树的实现,及其平衡的过程.

二

     平衡的算法思想其实非常简单, 就是将不平衡的二叉树, 通过旋转使其平衡. 下面举个简单的列子,大家就会明白了.

     

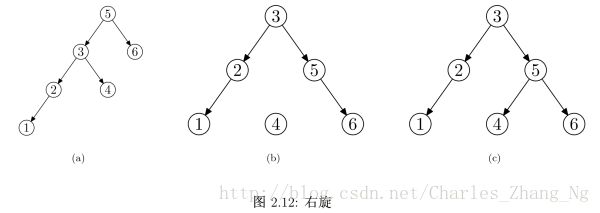
      相比于基本的二叉查找树不同的是,AVL树中多了一个'平衡因子'的数据, 它是用来记录当前节点的左子树和右子树高度的差值. 平衡因子 <  2 , 当 >=2 我们就要进行旋转 , 首先看2.13 (a) 图, 在二叉查找树中, 插入 5, 6, 3, 4, 2 ,1  可以看到树是不平衡的. 且根节点5 的平衡因子 = 2 需要旋转, 由于左子树比右子树高, 所以应当右旋 , 右旋以左子(3) 为父,父(5)为右子,可以得到图2.12(b). 这时(5)这个节点的左孩子应当指向(3)的右孩子, 即 右孙(4)变左孙, 经过此次右旋后得到图2.12 (c). 左旋同理, 以 4, 3, 6 , 5, 7 ,8 在纸上模拟一下左旋的操作

                                              

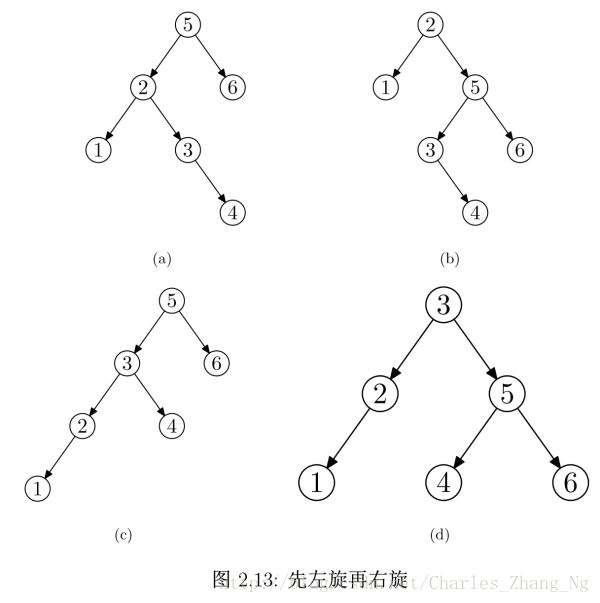
      但如果我们将 5, 2 ,6 ,1,  3, 4 插入可以得到图2.13(a),和刚才一样进行右旋操作的时候会得到图2.13(b). 这和没有旋转没有区别.因为高度差还是2. 且(2)节点的平衡因子为 -1 , 这时就不能直接旋转. 但可以转化为图2.12(a) 然后在进行右旋, 在图2.13(a) 中将 (3) 节点进行左旋 就可以啦.然后进行右旋就平衡了. 同理可用 4, 3, 7 , 6, 5, 8 进行反向操作.

                                       

旋转的思想讲完了, 下面上插入代码. 由于删除操作 实在原有的二叉查找树中删除后重新平衡, 与插入相类似.,就不放代码了. 本文章源码在github中可自行下载.https://github.com/ZhangSiQihandsome/Data-Structure.git

// 节点信息
struct Node{
        Key key;
        int depth;
        int balance;
        Node* parent;
        Node* left;
        Node* right;

        Node(Key data){
            this->key = data;
            depth = 1;
            balance = 0;
            left = NULL;
            right = NULL;
            parent = NULL;
        }

        Node(Node* node){
            key = node->key;
            depth = 1;
            balance = 0;
            parent = NULL;
            left = NULL;
            right = NULL;
        }
    };

// public 插入函数
void insert(Key data){
        if( root == NULL ){
            root = new Node(data);
            count++;
            return;
        }
        insert(root, data);
    }

// privat 插入函数
void insert( Node* node, Key data ){
        if( data < node->key ){
            if( node->left != NULL )
                insert(node->left, data);
            else{ // 左节点为空
                Node* node1 = new Node(data);
                node1->parent = node;
                node->left = node1;
                count++;
            }
        }
        else if( data > node->key ){
            if( node->right != NULL )
                insert( node->right , data );
            else{
                Node* node1 = new Node(data);
                node1->parent = node;
                node->right = node1;
                count++;
            }
        }
        // 将插入后的二叉树进行平衡调整
        Balance(node);
    }

// 右旋    

void right_rotate( Node* node ){
        // 一次旋转涉及到的节点包括 双亲,左子做父,右孙
        Node* pParent = node->parent, *pLeftSon = node->left, *pLeftGrandSon = pLeftSon->right;

        // 左子做父
        pLeftSon->parent = pParent;
        if( pParent != NULL ){  // 存在父节点
            if( node == pParent->left )  // node 为左子
                pParent->left = pLeftSon;  // 将 node -> parent -> left 指向 node -> left
            else if( node == pParent->right ) // node 为右子
                pParent->right = pLeftSon;
        }
        else
            root = pLeftSon;
        // 根为右子
        pLeftSon->right = node;
        node->parent = pLeftSon;

        // 右孙 变 左孙
        node->left = pLeftGrandSon;
        if( pLeftGrandSon != NULL )
            pLeftGrandSon->parent = node;

        // 重新计算平衡因子
        node->depth = calcDepth(node);
        node->balance = calcBalance(node);

        pLeftSon->depth = calcDepth(pLeftSon);
        pLeftSon->balance = calcBalance(pLeftSon);
    }

// 左旋
void left_rotate( Node* node ){
        // 一次旋转设计到的节点包括 双亲, 右子做父, 左孙
        Node* pParent = node->parent, *pRightSon = node->right,*pRightGrandSon = pRightSon->left;

        // 右子做父
        pRightSon->parent = pParent;
        if( pParent != NULL ){
            if( node == pParent->left )
                pParent->left = pRightSon;
            else if( node == pParent->right )
                pParent->right = pRightSon;
        }
        else
            root = pRightSon;
        // 根为左子
        pRightSon->left = node;
        node->parent = pRightSon;

        // 左孙 变 右孙
        node->right = pRightGrandSon;
        if( pRightGrandSon != NULL )
            pRightGrandSon->parent = node;

        // 重新计算平衡因子
        node->depth = calcDepth(node);
        node->balance = calcBalance(node);

        pRightSon->depth = calcDepth(pRightSon);
        pRightSon->balance = calcBalance(pRightSon);
    }

void Balance(Node*node){
        node->balance = calcBalance(node);

        // 左子树高,应该右旋
        if( node->balance >= 2 ){
            // 如果左子树右孙高, 先左旋
            if( node->left->balance == -1 )
                left_rotate(node->left);
            // 右旋
            right_rotate(node);
        }

        if( node->balance <= -2 ){
            // 如果右子树左孙高,先右旋
            if(node->right->balance == 1)
                right_rotate( node->right );
            // 左旋
            left_rotate(node);
        }

        node->balance = calcBalance(node); // 重新计算平衡因子
        node->depth = calcDepth(node);     // 重新计算当前节点深度
    }

// 高度差
int calcBalance(Node* node){  // 以传入的node节点为根 计算左右两字数的高度差
        int left_depth;
        int right_depth;

        if( node->left != NULL )
            left_depth = node->left->depth;
        else left_depth = 0;
        if( node->right != NULL )
            right_depth = node->right->depth;
        else right_depth = 0;

        return left_depth - right_depth;
    }

// 深度
int calcDepth( Node* node ){ // 计算当前节点为根节点 高度高的子树深度
        int depth = 0;
        if( node->left != NULL )
            depth = node->left->depth;

        if( node->right != NULL && depth < node->right->depth )
            depth = node->right->depth;

        depth++;
        return depth;
    }