Codevs1515 跳

题目描述 Description
邪教喜欢在各种各样空间内跳。

现在，邪教来到了一个二维平面。在这个平面内，如果邪教当前跳到了(x,y)，那么他下一步可以选择跳到以下4个点：(x-1,y), (x+1,y), (x,y-1), (x,y+1)。

而每当邪教到达一个点，他需要耗费一些体力，假设到达(x,y)需要耗费的体力用C(x,y)表示。

对于C(x,y)，有以下几个性质：

1、若x=0或者y=0，则C(x,y)=1。

2、若x>0且y>0，则C(x,y)=C(x,y-1)+C(x-1,y)。

3、若x<0且y<0，则C(x,y)=无穷大。

现在，邪教想知道从(0,0)出发到(N,M)，最少花费多少体力（到达(0,0)点花费的体力也需要被算入）。

由于答案可能很大，只需要输出答案对10^9+7取模的结果。

输入描述 Input Description
读入两个整数N，M，表示邪教想到达的点。

输出描述 Output Description
输出仅一个整数，表示邪教需要花费的最小体力对10^9+7取模的结果。

样例输入 Sample Input
1 2

样例输出 Sample Output
6

数据范围及提示 Data Size & Hint
对于10%的数据，满足N, M<=20；

对于30%的数据，满足N, M<=100；

对于60%的数据，满足min(N,M)<=100；

对于100%的数据，满足0<=N, M<=10^12，N*M<=10^12。

代码Code

#include
#include
#define LL long long
using namespace std;
LL p = 1e9+7;

LL ksm(LL a,LL k){
    if(!k) return 1;
    LL b = 1;
    while(k){
        if(k&1) b = (b*a)%p;
        k /= 2;
        a = (a*a)%p;
    }
    return b;
}

LL C(LL n,LL m){

    if(m > n) return 0;

    LL upon = 1,down = 1;

    for(LL i = n;i > n-m;i--) upon = upon*i%p;

    for(LL i = 2;i <= m;i++) down = down*i%p;

    return (upon*ksm(down,p-2))%p;
}

LL Lucas(LL n,LL m){
    if(!m) return 1;
    else return C(n%p,m%p)*Lucas(n/p,m/p);
}

int main(){

    LL x,y;
    scanf("%lld%lld",&x,&y);

    if(x < y) swap(x,y);
    printf("%lld",(x+Lucas(x+y+1,y))%p);

    return 0;
}

分析

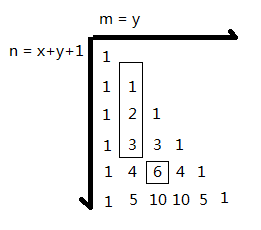
显然题目的那张地图就是杨辉三角，主要问题是求解某个组合数。如图，x&y是原题的坐标系元素，现在改成n&m坐标系方便用杨辉三角的组合数性质。显然最短的路径就是先走一段11111..然后直接往下走。如果要求的是到图中值为3的点(1,2)的最短路径，通过某些不可描述的方法发现那段框起来的数总和为右下角那个被框起来的6，就是于是有C(n,m)+C(n-1,m)+….+C(m,m) = C(n+1,m+1)。

理论基础
Lucas定理+杨辉三角+逆元
（这里用了费马小定理求逆元，那么还有：费马小定理+快速幂）