第13届东北地区大学生程序设计竞赛 赛后补题

心得

感觉自己前中期题还是很不熟练，有很多基础的东西应该掌握，

所以还是巩固基础，别太死抠难题怪题，有空也多补一下队友的思路和做法

 

C.Line-line Intersection(计算几何基础)

n(n<=1e5)条直线，第i条用(x1i,y1i),(x2i,y2i)两个点表示，

问你有多少对直线有交点，重合也算有交点

 

相交=总-平行+重合，平行是把重合的情况多减了，所以加回来就好

存成ax+by+c=0的形式，注意特判x1==x2的情况，此时存成x==x1即1x+0y-x1=0的形式

除以gcd的时候，要保证gcd非负，且最后优先a正，a==0时b正

似乎还有make_tuple的STL写法，回头再学好了咕咕咕

#include
using namespace std;
#define x1 pp1
#define x2 pp2
#define y1 qq1
#define y2 qq2
typedef long long ll;
typedef pair pl;
typedef pair pll;
//ax+by+c=0;
int t,n;
ll x1,x2,y1,y2,a,b,c,g,gg,ans;
mapmp;
mapmpp;
ll gcd(ll a,ll b)
{
	return b?gcd(b,a%b):a;
} 
int main()
{
	scanf("%d",&t);
	while(t--)
	{
		mp.clear();
		mpp.clear();
		scanf("%d",&n);
		for(int i=1;i<=n;++i)
		{
			scanf("%lld%lld%lld%lld",&x1,&y1,&x2,&y2);
			a=y2-y1;b=x1-x2;c=x2*y1-x1*y2;
			if(b==0)a=1,c=-x1;//x==x1 
			g=(gcd(gcd(a,b),c));
			a/=g;b/=g;c/=g;
			if(a<0||(a==0&&b<0))a=-a,b=-b,c=-c;
			gg=abs(gcd(a,b));
			mp[pl(a/gg,b/gg)]++;
			mpp[pll(pl(a,b),c)]++;
		}
		ans=1ll*n*(n-1)/2;
		for(map::iterator it=mp.begin();it!=mp.end();it++)
		{
			ll num=it->second;
			ans-=num*(num-1)/2;
		}
		for(map::iterator it=mpp.begin();it!=mpp.end();it++)
		{
			ll num=it->second;
			ans+=num*(num-1)/2;
		}
		printf("%lld\n",ans);
	}
	return 0;
}

E.minimum spanning tree(最小生成树/线图)

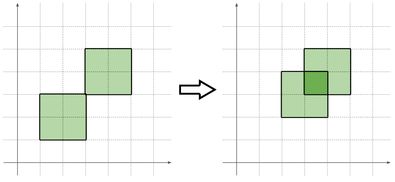
图G的线图L(G)定义为，把G中的所有边变成L(G)中的点，

G中两条边如果有公共顶点，就在L(G)中两条边对应的两个点之间连一条边，

L(G)中边的代价为原图中两条边的代价之和

 

给你一棵n(n<=1e5)个点的树G，让你求线树L(G)的最小生成树，

n-1条边以u v w的形式给出，w<=1e9

共T(T<=1e3)组样例，保证n的总数不超过1e6

 

考虑最极端的菊花图情形，与根相连的边，在线图中构成了一个团

由于，在L(G)中的点的代价为G中对应边的代价，构成点的最小生成树，

只需让所有点都连向代价最小的点即可，

如果有n个点，n-1条边，代价最小的点被计n-1次，其余1次，即总和+(n-2)代价最小点的代价

仔细观察可以发现，L(G)中不同团之间，只会有公共点而无公共边，

所以分别计算，每个团的最小生成树的代价，最后求和即可

#include
using namespace std;
typedef long long ll;
const int maxn=1e5+10;
vectorV[maxn];
int t,n,u,v;
ll w,ans,mn[maxn];
int main()
{ 
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d",&n);
		ans=0;
		for(int i=1;i<=n;++i)
		{
			mn[i]=1e18;
			V[i].clear();
		}
		for(int i=1;i=2 团两两之间都有边 生成树随便连
		//因此，团的最小生成树是每条边都连向边权最小的边  
		//因此，该值=所有边之和+(与点相连的边的条数-2)*最小边权 
		for(int i=1;i<=n;++i)
		{
			int len=V[i].size();
			//printf("%d:%d\n",i,len);
			if(len<2)continue;
			for(int j=0;j

 

G.Radar Scanner(三分or中位数)

一共有n(n<=1e5)个矩形，第i个矩形以左下角(ai,bi)，右上角(ci,di)的形式给出

格子的坐标，实际上是格子右上角那个点的坐标

将矩形挪动使得所有矩形都覆盖至少一个矩形，挪动的代价为挪动的曼哈顿距离，

求最小的代价和，输出代价和

共T(T<=1e3)组样例，保证n的总数不超过1e6

 

赛中的时候三分过的，但实际有更简单的做法

由于最后选的方格不一定要在已有矩形内部，所以可以任取，这就表明x和y是独立的

把二维降到一维，一维问题中，只需挪到中位数的位置即可，那独立的二维也一样

注意判断，这个点是否已经在矩形区域中了，在就不计入代价

#include
using namespace std;
#define x1 pp1
#define x2 pp2
#define y1 qq1
#define y2 qq2
typedef long long ll;
const int N=1e5+10;
int t,n,x[N<<1],y[N<<1];
int x1[N],x2[N],y1[N],y2[N];
int midx,midy,tx,ty;
ll ans;
int main()
{
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d",&n);
		for(int i=1;i<=n;++i)
		{
			scanf("%d%d",&x1[i],&y1[i]);
			scanf("%d%d",&x2[i],&y2[i]);
			x[i]=x1[i];y[i]=y1[i];
			x[i+n]=x2[i];y[i+n]=y2[i];
		} 
		sort(x+1,x+2*n+1);sort(y+1,y+2*n+1);
		midx=x[n];midy=y[n];
		ans=0;
		for(int i=1;i<=n;++i)
		{
			if((tx=max(x1[i],x2[i]))midx)ans+=tx-midx;
			if((ty=max(y1[i],y2[i]))midy)ans+=ty-midy;
		}
		printf("%lld\n",ans);
	}
	return 0;
}

 

H.Skyscraper(差分)

n(n<=1e5)个数，第i个数为ai(1<=ai<=1e5)

以下m(m<=1e5)个操作，操作分两种

1 l r k 对区间[l,r]，将ai变为ai+k(1<=k<=1e5)

2 l r 询问[l,r]内最少需要几次操作使得每个数hi都能变为ai

每次询问初始时，hl=...=hr=0，每次你可以选择一个子区间[L,R]，将其区间+1，视为一次操作

共T(T<=1e3)组样例，保证n的总数不超过1e6，m的总数不超过1e6

 

从前到后考虑这个拔高的过程，考虑后项对前项的差分，

那只有正的项需要再新开操作次数，负的项是可以从前面的操作中获益的

维护两个BIT，差分BIT和差分正项BIT（正项为其对应值 其余位置为0），

区间+k即为差分BIT两个单点的修改，

如果产生正负项的变化，再去差分正项BIT里进行修改

那[l,r]内的操作数，即为l的操作数加上后面差分项里正项的操作数

l的操作数在差分BIT上求，是al此刻的值，后者在差分正项BIT里求

 

搞了两个差分+BIT，都能过，BIT的不同写法吧，后者是按题解搞的

#include
#include
#include
#include
#include
#include 
#include

#include
#include
#include
#include
#include
#include 
#include