贝叶斯公式，最大似然估计，最大后验估计，EM算法

贝叶斯公式

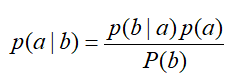
在此处，我们换一下表示符号：
下列符号表达的含义是和下文相关的，所以可以在此先不深究其含义

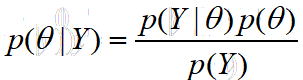
其中：
1、Y={y1,y2,……，yn}代表一组样本，是对某个数据总体所有变量的每一个随机采样一个值得到的样本。这个样本满足独立同分布（iid）
2、theta代表一种分布模型的参数，可能是一个数，也可能是一个向量（例如，GAUSS分布的参数为（均值，方差），这样便是一个两元素向量）
3、p(theta|Y)，被称为后验概率，此处的含义是，我们已获得了一组样本，在此基础之上，我们推测样本所满足的模型的参数是theta的概率。
4、p(Y|theta),被称为似然（这个词可以理解为“很像”），此处的含义是，模型的参数为theta时，随机采样获得的一组样本恰好是Y的概率。
5、p(theta)、p(Y)，被称为先验，含义很明确，就不展开说了，用处也不大。

最大似然估计

MLE(Maximun Likelihood Estimation)，也成为极大似然估计，是统计学的一种方法。即，是一种从数据出发，计算数据所满足的模型的性质的方法。

作用

我们要干个什么事呢？

假设我们已有一组样本Y，这个样本是从某个数据总体（这个样本总体的变量是y1,y2,……，yn，每个变量由一个或多个按概率可取的值）中随机采样获得的（或者是由某种生成数据的（概率）规则生成的）。

除此之外，我们还知道这个数据总体（或规则）所满足的概率模型的类型。
这里要说明一下，在实际问题中（我们所遇到的所有问题中）这个模型是我们猜测的，而不是真正的，是绝对不可能完全精确的反映样本总体的。原因是，样本可能有噪声，或者数据总体本身就不存在一个模型。所以，我们只能假设一个最有可能且好计算的模型，比如假设概率分布为高斯函数。当然我们猜测的规则而不是样本总体时可能会简单一点，比如一系列布尔概率变量组成的规则。

我们希望知道的是，这个模型的具体参数是什么？ 由于模型的类型是猜测假设的，所以我们也就不可能获得真正模型的真正的参数，我们所能做到是，获得一个尽可能对的模型参数，也就是说获得一个尽可能符合样本的模型参数。

MLE就是完成这个任务的一种算法。简单来说，MLE办了这么一个事：
样本+模型类型——>模型参数

原理

那MLE是怎么办到的呢？

我们先回过头来看看刚才提到的作用，我们已知的是样本和模型类型，先不管模型类型，我们看看样本是什么，回顾贝叶斯公式部分，样本就是我们定义的Y。

我们想求得是什么？模型参数，正好是theta。

至于模型类型，这个会暗含在之后计算概率的公式中。

所以说我们想要的是：后验概率p(theta|Y) 由于上面我们提到的模型是假设的这一原因，此处我们对应的说法应该是：我们想要的是使得后验概率最大的Theta

遗憾的是，p(theta|Y)并不能直接计算，因为我们并不知道它的具体表达式（你可以试试，如果发现不知道怎么计算，那就继续往下看，看看MLE是怎么解决的）

显然我们要用到贝叶斯公式，而且是用贝叶斯公式等号右边部分来代替p(theta|Y)。

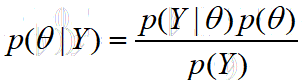
记住，我们要求的是最大的p(theta|Y)对应的theta，而不是p(theta|Y)，所以分母就可以去掉了，因为它不影响我们比较哪个theta对应的p(theta|Y)最大。所以，我们的目标就变成了p(Y|theta)p(theta)。

遗憾的是，p(theta)通常我们也不知道。于是，我们想当然的想到：如果使得p(Y|theta)最大的theta正好是使得p(theta|Y)最大的theta，那该多好啊。幸运的是，这种想法是有道理的，具体地说是在某些情况下精确可行的，某些情况下，精度下降可行的。

所以，我们的任务成为了找到使p(Y|theta)最大的theta。p(Y|theta)的名字是似然，所以这种方法称为最大似然估计

计算

那为什么，p(Y|theta)就是好算的呢，或者说它的表达式是什么呢。就像我们最开始提到的，p(Y|theta)的含义是：模型的参数为theta时，随机采样获得的一组样本恰好是Y的概率。就是说已知模型的具体参数，问你产生某个样本的概率是多少？显然这是我们擅长的。

需要注意的是，Y={y1,y2,……，yn}，它是一组样本，我们真正要求的是：
p( y1,y2,……，yn|theta)
emmmmmm，怎么刚说了好求，接着就不会求了呢。。。

莫慌，我们在最开始解释Y的含义时，提到了这么一句：这个样本满足独立同分布（iid）。
显然：p( y1,y2,……，yn|theta)=p( y1|theta)p( y2|theta)，……，p( yn|theta)
其中p( yi|theta)的具体形式是由我们假设的模型给出的

进一步解释一下，p(Y|theta)是一个以theta（可能是一个变量，也可能是多个变量）为自变量的方程。

我们为了获得使p(Y|theta)最大的theta，只需将p(Y|theta)对theta求导。当然为了计算简便，我们通常取log(p(Y|theta))计算。

最大后验估计

MAP(maximum a posteriori estimation)，它的作用和MLE完全一致，算法只是在MLE基础上增加了一个量。

还记得我们之前提到过的，我们本该计算p(Y|theta)p(theta)，但因为不知到p(theta)的值，于是想当然的只计算p(Y|theta)。对，这里增加的量就是p(theta)。

MAP就是在MLE的情形下，我们能够知道p(theta)，于是我们就用p(Y|theta)p(theta)去求咯，就这么简单。

因为p(Y|theta)p(theta)确实能精确反映不同theta下的后验概率p(theta|Y)的大小，所以称为最大后验估计。

EM算法

均值最大化（Expectation Maximization）算法。它也是从最大似然算法来的，与最大后验估计不同，EM是在MLE上减少了条件。少的是哪部分呢？

回顾之前提到的Y的定义：Y={y1,y2,……，yn}代表一组样本，是对某个数据总体所有变量的每一个随机采样一个值得到的样本。这个样本满足独立同分布（iid）。
这里少的是Y中的一部分元素，也就是说Y不再包含所有的变量，只是数据总体部分变量大随机采样值。简单起见，这里我们仍用Y={y1,y2,……，yn}表示。并定义少的那部分，或称未观测到的那部分为Z={z1,z2,……，zn}，称之为隐含变量，这里Y和Z一起构成了数据总体的所有变量。

需要指出的是遇到这样一个问题时，我们并不知道Y是否包含了全部变量，也就是说我们不知道是否有Z的存在，跟不知道Z有几个变量。为简单起见，下文推导只将Z看成一个变量

那么在丢失了一部分的情况下，EM算法是怎么计算p(theta|Y)的呢？

EM算法原理

EM算法是一种迭代算法。
懒得写了，我理解这个算法主要参考了

https://blog.csdn.net/livecoldsun/article/details/40833829

我的总结，就不细说了