李宏毅机器学习 Machine_Learning_2019_Task 5
李宏毅机器学习 Machine_Learning_2019_Task 5
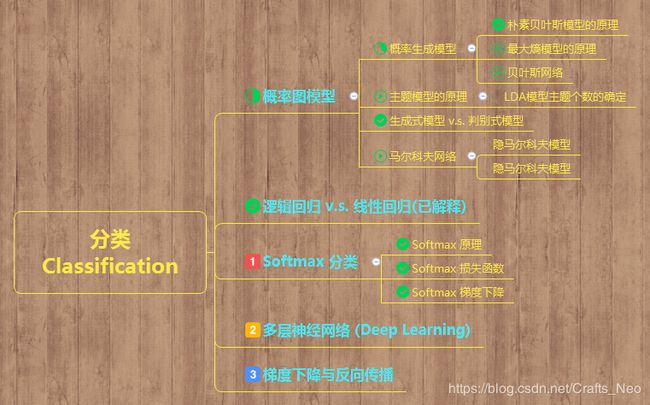
学习导图
学习内容
-
LR(Logistic Regression) 学习
Logistic 函数是一个概率分布函数，即给定某个特定输入，该函数将计算输出为“Success”的概率，即对问题的回答为“Yes”的概率。
-
推导 LR损失函数(已推导参考前期Task)
Logistic 回归模型估计概率(向量形式)
p ^ = h θ ( x ) = σ ( x T θ ) \hat{p}=h_{\theta}(\mathbf{x})=\sigma\left(\mathbf{x}^{T} \boldsymbol{\theta}\right) p^=hθ(x)=σ(xTθ)
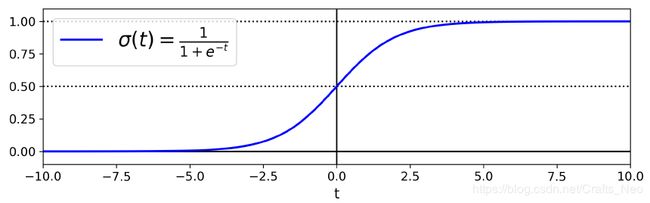
Logistic 函数
σ ( t ) = 1 1 + exp ( − t ) \sigma(t)=\frac{1}{1+\exp (-t)} σ(t)=1+exp(−t)1t = np.linspace(-10, 10, 100) sig = 1 / (1 + np.exp(-t)) plt.figure(figsize=(9, 3)) plt.plot([-10, 10], [0, 0], "k-") plt.plot([-10, 10], [0.5, 0.5], "k:") plt.plot([-10, 10], [1, 1], "k:") plt.plot([0, 0], [-1.1, 1.1], "k-") plt.plot(t, sig, "b-", linewidth=2, label=r"$\sigma(t) = \frac{1}{1 + e^{-t}}$") plt.xlabel("t") plt.legend(loc="upper left", fontsize=20) plt.axis([-10, 10, -0.1, 1.1]) # save_fig("logistic_function_plot") plt.show()
-
Logistic function
Logistic 回归模型预测
y ^ = { 0 if p ^ < 0.5 1 if p ^ ≥ 0.5 \hat{y}=\left\{\begin{array}{l}{0 \text { if } \hat{p}<0.5} \\ {1 \text { if } \hat{p} \geq 0.5}\end{array}\right. y^={0 if p^<0.51 if p^≥0.5
Logistic 回归模型的损失函数
- 平方误差
L ( f ) = 1 2 ∑ n ( f w , b ( x n ) − y ^ n ) 2 L(f)=\frac{1}{2} \sum_{n}\left(f_{w, b}\left(x^{n}\right)-\hat{y}^{n}\right)^{2} L(f)=21n∑(fw,b(xn)−y^n)2
其中，
f w , b ( x ) = σ ( ∑ i w i x i + b ) f_{w, b}(x)=\sigma\left(\sum_{i} w_{i} x_{i}+b\right) fw,b(x)=σ(i∑wixi+b)
-
交叉熵损失函数
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( p ^ ( i ^ ) ) + ( 1 − y ( i ) ) log ( 1 − p ^ ( i ) ) ] J(\boldsymbol{\theta})=-\frac{1}{m} \sum_{i=1}^{m}\left[y^{(i)} \log \left(\hat{p}^{(\hat{i})}\right)+\left(1-y^{(i)}\right) \log \left(1-\hat{p}^{(i)}\right)\right] J(θ)=−m1i=1∑m[y(i)log(p^(i^))+(1−y(i))log(1−p^(i))]
对模型参数求偏导
∂ ∂ θ j J ( θ ) = 1 m ∑ i = 1 m ( σ ( θ T x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial}{\partial \theta_{j}} \mathrm{J}(\theta)=\frac{1}{m} \sum_{i=1}^{m}\left(\sigma\left(\theta^{T} \mathbf{x}^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)} ∂θj∂J(θ)=m1i=1∑m(σ(θTx(i))−y(i))xj(i)
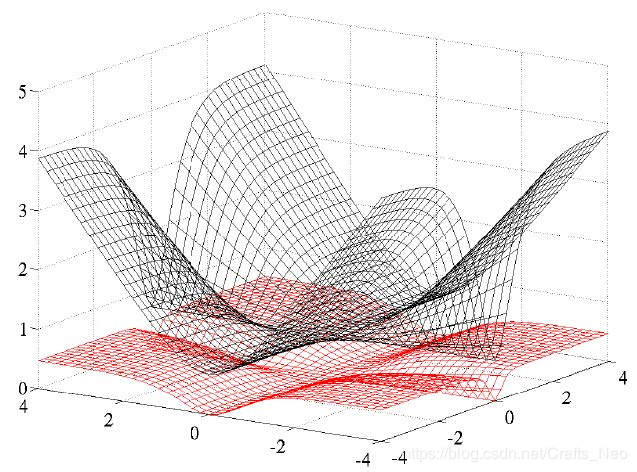
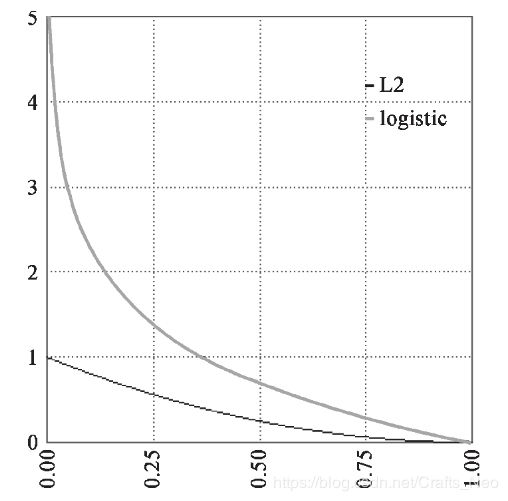
交叉熵与平方误差
Cross Entropy VS Square Error
-
学习 LR 梯度下降
Logistic 回归模型、最大熵模型可归结为以似然函数为目标函数的最优化问题，通常通过迭代算法求解，它
是光滑的凸函数，因此多种最优化的方法都能适用。-
常用方法：
- 梯度下降法
- 改进的迭代尺度法
- Newton 法
- 拟 Newton 法
-
梯度下降法
梯度下降法是一种迭代算法.选取适当的初始值x(0)，不断迭代，更新x的值，进行目标函数的极小化，直到收敛。由于负梯度方向是使函数值下降最快的方向，在迭代的每一步，以负梯度方向更新x的值，从而达到减少函数值的目的。
-
假设f(x)具有一阶连续偏导数的函数
min x ∈ R n f ( x ) \min _{x \in \mathbb{R}^{n}} f(x) x∈Rnminf(x) -
一阶泰勒展开
f ( x ) = f ( x ( k ) ) + g k T ( x − x ( k ) ) f(x)=f\left(x^{(k)}\right)+g_{k}^{\mathrm{T}}\left(x-x^{(k)}\right) f(x)=f(x(k))+gkT(x−x(k)) -
f(x)在x(k)的梯度值
g k = g ( x ( k ) ) = ∇ f ( x ( k ) ) x ( k + 1 ) ← x ( k ) + λ k p k \begin{array}{c}{g_{k}=g\left(x^{(k)}\right)=\nabla f\left(x^{(k)}\right)} \\ {x^{(k+1)} \leftarrow x^{(k)}+\lambda_{k} p_{k}}\end{array} gk=g(x(k))=∇f(x(k))x(k+1)←x(k)+λkpk -
负梯度方向
p k = − ∇ f ( x ( k ) ) f ( x ( k ) + λ k p k ) = min λ ≥ 0 f ( x ( k ) + λ p k ) \begin{array}{c}{p_{k}=-\nabla f\left(x^{(k)}\right)} \\ {f\left(x^{(k)}+\lambda_{k} p_{k}\right)=\min _{\lambda \geq 0} f\left(x^{(k)}+\lambda p_{k}\right)}\end{array} pk=−∇f(x(k))f(x(k)+λkpk)=minλ≥0f(x(k)+λpk)
-
-
-
利用代码描述梯度下降
from sklearn.linear_model import LogisticRegression clf = LogisticRegression(max_iter=200) clf.fit(X_train, y_train) clf.score(X_test, y_test) x_ponits = np.arange(4, 8) y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1] plt.plot(x_ponits, y_) plt.plot(X[:50, 0], X[:50, 1], 'bo', color='blue', label='0') plt.plot(X[50:, 0], X[50:, 1], 'bo', color='orange', label='1') plt.xlabel('sepal length') plt.ylabel('sepal width') plt.legend() -
Softmax 分类
Softmax 是 Logistic 回归在C个可能不同的值上的推广，
f ( x ) c = e − x c ∑ j = 0 C − 1 e − x j , c = 0 , ⋯ , C − 1 f(x)_{c}=\frac{\mathrm{e}^{-x_{c}}}{\sum_{j=0}^{C-1} \mathrm{e}^{-x_{j}}}, c=0, \cdots, C-1 f(x)c=∑j=0C−1e−xje−xc,c=0,⋯,C−1- 该函数的返回值为含C个分量的概率向量，每个分量对应于一个输出类别的概率；
- 由于各分量为概率，C个分量之和始终为1，这是因为softmax的公式要求每个样本必须属于某个输出类别，且所有可能的样本均被覆盖；
- 如果各分量之和小于1，则意味着存在一些隐藏的类别；
- 若各分量之和大于1，则说明每个样本可能同时属于多个类别；
- 换言之，当类别总数为2时，所得到的输出概率与 Logistic 回归模型的输出完全相同。
-
Softmax原理(已解释)
-
Softmax损失函数
- 对于单个训练样本i，交叉熵的形式变为
loss i = − ∑ c ( y c ⋅ log ( y − predicted c ) ) \operatorname{loss}_{i}=-\sum_{c}\left(y_{c} \cdot \log \left(y_{-} \text { predicted }_{c}\right)\right) lossi=−c∑(yc⋅log(y− predicted c))
将每个输出类别在训练样本上的损失相加。
Note: 对于训练样本的期望类别，yc应当为1，对其他情形应为0，因此实际上这个和式中只有一个损失值被计入，它度量了模型为真实类别预测的概率的可信度!!!
- 为计算训练集上的总损失值，考虑将每个训练样本的损失相加
loss = − ∑ c ∑ c ( y c i ⋅ log ( y − predicted c i ) ) \operatorname{loss}=-\sum_{c} \sum_{c}\left(y_{c_{i}} \cdot \log \left(y_{-} \text { predicted }_{c_{i} )}\right)\right. loss=−c∑c∑(yci⋅log(y− predicted ci))
-
Softmax梯度下降
from sklearn.linear_model import LogisticRegression X = iris["data"][:, (2, 3)] # petal length, petal width y = (iris["target"] == 2).astype(np.int) log_reg = LogisticRegression(solver="lbfgs", C=10**10, random_state=42) log_reg.fit(X, y) x0, x1 = np.meshgrid( np.linspace(2.9, 7, 500).reshape(-1, 1), np.linspace(0.8, 2.7, 200).reshape(-1, 1), ) X_new = np.c_[x0.ravel(), x1.ravel()] y_proba = log_reg.predict_proba(X_new) plt.figure(figsize=(10, 4)) plt.plot(X[y==0, 0], X[y==0, 1], "bs") plt.plot(X[y==1, 0], X[y==1, 1], "g^") zz = y_proba[:, 1].reshape(x0.shape) contour = plt.contour(x0, x1, zz, cmap=plt.cm.brg) left_right = np.array([2.9, 7]) boundary = -(log_reg.coef_[0][0] * left_right + log_reg.intercept_[0]) / log_reg.coef_[0][1] plt.clabel(contour, inline=1, fontsize=12) plt.plot(left_right, boundary, "k--", linewidth=3) plt.text(3.5, 1.5, "Not Iris-Virginica", fontsize=14, color="b", ha="center") plt.text(6.5, 2.3, "Iris-Virginica", fontsize=14, color="g", ha="center") plt.xlabel("Petal length", fontsize=14) plt.ylabel("Petal width", fontsize=14) plt.axis([2.9, 7, 0.8, 2.7]) # save_fig("logistic_regression_contour_plot") plt.show() X = iris["data"][:, (2, 3)] # petal length, petal width y = iris["target"] softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10, random_state=42) softmax_reg.fit(X, y) x0, x1 = np.meshgrid( np.linspace(0, 8, 500).reshape(-1, 1), np.linspace(0, 3.5, 200).reshape(-1, 1), ) X_new = np.c_[x0.ravel(), x1.ravel()] y_proba = softmax_reg.predict_proba(X_new) y_predict = softmax_reg.predict(X_new) zz1 = y_proba[:, 1].reshape(x0.shape) zz = y_predict.reshape(x0.shape) plt.figure(figsize=(10, 4)) plt.plot(X[y==2, 0], X[y==2, 1], "g^", label="Iris-Virginica") plt.plot(X[y==1, 0], X[y==1, 1], "bs", label="Iris-Versicolor") plt.plot(X[y==0, 0], X[y==0, 1], "yo", label="Iris-Setosa") from matplotlib.colors import ListedColormap custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0']) plt.contourf(x0, x1, zz, cmap=custom_cmap) contour = plt.contour(x0, x1, zz1, cmap=plt.cm.brg) plt.clabel(contour, inline=1, fontsize=12) plt.xlabel("Petal length", fontsize=14) plt.ylabel("Petal width", fontsize=14) plt.legend(loc="center left", fontsize=14) plt.axis([0, 7, 0, 3.5]) # save_fig("softmax_regression_contour_plot") plt.show()
-
多层神经网络 (MLNNs-Deep Learning)
线性回归模型和 Logistic 回归模型本质上都是单个神经元，它具有以下功能：
计算输入特征的加权和。可将偏置视为每个样本中输入特征为1的权重，称之为计算特征的线性组合；
运用一个激活函数并计算输出。对于线性回归的例子，激活函数保持值不变，而 Logistic 回归将Sigmoid函数作为激活函数。
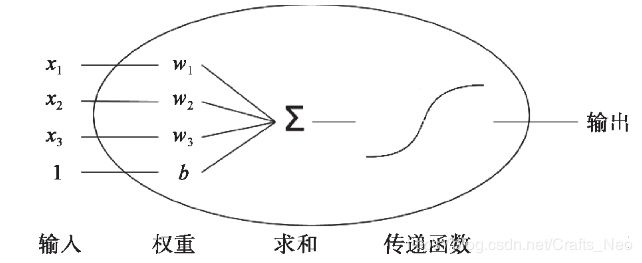
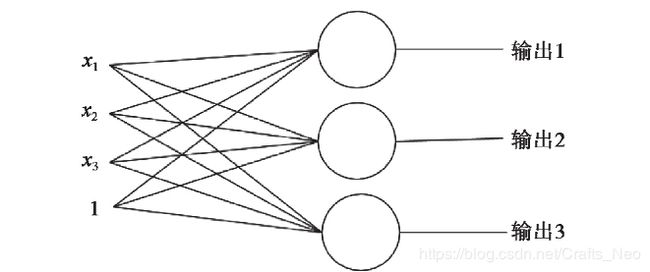
单个神经元结构
每个神经元的输入、处理和输出
Softmax 分类
对于softmax分类，使用了一个含C个神经元的网络，其中每个神经元对应一个可能的输出类别
-
梯度下降与反向传播
- 梯度下降法是一种致力于找到函数极值点的算法。所谓“学习”便是改进模型参数，以便通过大量训练步骤将损失最小化。换言之，即将梯度下降法应用于寻找损失函数的极值点便构成了依据输入数据的模型学习。
梯度下降算法定义为：
weights stepi + 1 = weights stepi − η ∇ loss ( weights step i ) \text {weights}_{\text {stepi}+1}=\text {weights}_{\text {stepi}}-\eta \nabla \operatorname{loss}\left(\text { weights }_{\text { step }_{i}}\right) weightsstepi+1=weightsstepi−η∇loss( weights step i)-
反向传播算法
以一个单输入、单输出的极简网络为例，该网络拥有两个隐含层，每个隐含层都只含单个神经元。隐含层和输出层神经元的激活函数都采用了sigmoid，而损失将通过交叉熵来计算
简单的反向传播算法Note:
-
每一层的导数都是后一层的导数与前一层输出之积，这正是链式法则的奇妙之处，误差反向传播算法利用的正是这一特点；
-
前馈时，从输入开始，逐一计算每个隐含层的输出，直到输出层。然后开始计算导数，并从输出层经各隐含层逐一反向传播。为了减少计算量，还需对所有已完成计算的元素进行复用。这便是反向传播算法名称的由来。
-
参考 (理论 + 实践)
机器学习实战
李航统计学习
百面机器学习
Hands-on Machine Learning with Scikit-Learn, Keras & TensorFlow
TensorFlow for Machine Intelligence: A Hands-On Introduction to Learning Algorithm