简述
Matplotlib是一个基于python的2D画图库,能够用python脚本方便的画出折线图,直方图,功率谱图,散点图等常用图表,而且语法简单。具体介绍见matplot官网。
Numpy(Numeric Python)是一个模仿matlab的对python数值运算进行的扩展,提供了许多高级的数值编程工具,如:矩阵数据类型、矢量处理,以及精密的运算库。专为进行严格的数字处理而产生,而且据说自从他出现了以后,NASA就把很多原来用fortran和matlab做的工作交给了numpy来做了,可见其强大。。。他的官网在这里,具体的资料都在里面。
安装
$sudo apt-get install python-matplotlib $sudo apt-get install python-numpy
(牛力大法好~)
使用
matplotlib可以在脚本中使用,不过如果在ipython中使用则会更加炫(直接添加�Cpylab参数可以免去导包的过程),而且能得到类似Matlab/Mathematica一样的功能,即时输入,即时输出。个人觉得说白了他就是模仿Matlab/Mathematica的,但是的确比前者更加方便编程。
很多情况下matplot需要配合numpy包一起用,关于numpy包我不打算分开来说,用到的时候提一下就行。有一点需要注意的是,numpy包通常是这样导入的:
import numpy as np
会给他起一个叫np的别名,而且这几乎已经是约定俗成了。
在python或者ipython中输入help(*需要查找的函数*) 就行(当然需要先导入下包)。
第一个图像
需要导入的包:
import numpy as np from pylab import *
第一个函数图像
X = np.linspace(-np.pi, np.pi, 256,endpoint=True) C,S = np.cos(X), np.sin(X) plot(X,C) plot(X,S) show()
有matlab基础的同学肯定不陌生。。。是的,这两个模块的组合几乎就跟matlab的用法无二。。
1、首先用np.linspace方法生成一个数组X,这个数组是从$-\pi$开始到$\pi$的总共包含256个元素的数组,endpoint参数表示是否包含首尾端点(他的值是True或False,首字母要大写。。。。)。当然,这个数组就是一个普通的数组了,跟其他数组没有区别。
2、然后用np.cos()和np.sin()方法作用在X数组上,对于X中的每一个元素进行计算,生成结果数组。(免去了迭代的过程)。
3、接着调用pylab的plot方法,第一个参数是横坐标数组,第二个参数是纵坐标数组,其他参数暂且不谈。这样他会生成一个默认的图表了。(不会立刻显示)
4、当然,最后还要调用show方法来显示图表。
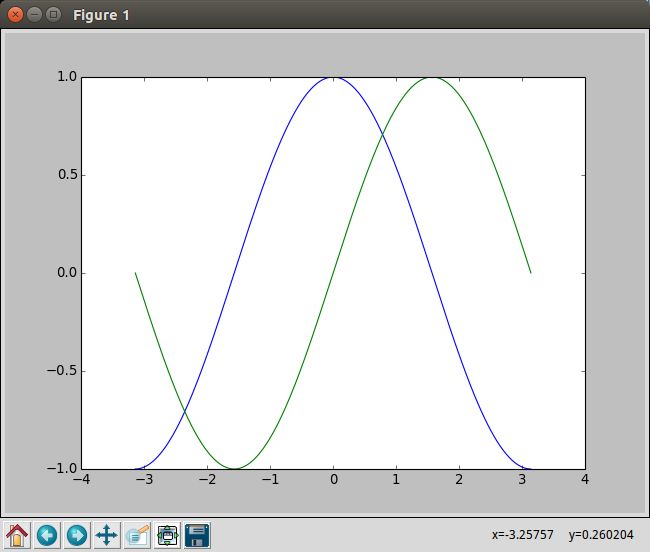
5、结果:
图表的名字叫figure1,左下面有几个按钮,都是很实用的东西,右下角会显示当前鼠标左边,也很方便。
图表布局和坐标分布
每一个图表都是在一个figure里面,我们可以通过如下命令生成一个空的figure:
figure(figsize=(8,6), dpi=80)
这里参数的顺序没有要求,但是一定要加上参数名,因为他是根据参数名来区别每个参数的,是一种跟C语言类型不同的函数。figsize参数表示figure的宽高比,然后dpi表示每一份占的长度,比如这里就表示图像是640x480的。
输出命令之后会立刻出现一个窗口,接下来所有的plot命令都会立刻显示在这个窗口上而不用再输入show命令了。
一个figure里也能显示多个图表,我们可以用如下函数来分割一个figure:
subplot(3,4,6)
这样就会把当前的figure分割成3行4列的表,而激活其中的第6张,即第2行第3张。以后的plot都是在这一个子表上生成的,如果需要更换则可以重新输入subplot命令来确定其新的位置。
除此之外,如果我们对图表显示的范围不满意,我们还可以直接调整图表的坐标范围:
xlim(-4.0,4.0) ylim(-1.0,1.0)
这就表示x轴的范围设置在-4到4,y轴的范围设置在-1到1。当然,如果是想相对的进行修改我们可以利用下numpy数组的min和max方法。比如X.min() 这样的东西。
如果对坐标显示的密度啊什么的不满意,我们也可以调节他的标注点:
xticks(np.linspace(-4,4,9,endpoint=True)) yticks(np.linspace(-1,1,5,endpoint=True))
对于xticks和yticks,我们实际上可以传入任意的数组,这里不过是为了方便而用numpy快速生成的等差数列。
当然,我们也可以给标注点进行任意的命名,像下面这样:
xticks([1,2,3,4,5],['one','two','three','four','five'])
效果也很好想象,就不贴图了。需要注意的是这里也可以支持LaTex语法,将LaTex引用在两个$之间就可以了。(关于LaTex)
这里也有个小窍门,就是如果想不显示标注的话,我们就可以直接给xticks赋一个空的数组。
更改色彩和线宽
我们可以在画plot的时候用如下方法指定他的颜色和线宽:
plot(X, C, color='#cadae3', linestyle='-',linewidth=1.3, marker='o', markerfacecolor='blue', markersize=12,)
同样,这里参数的顺序不重要,名字才重要。
color参数可以指定RGB的色相,也可以用一些默认的名字,比如red blue之类的。
linestyle参数则指定了线的样式,具体参照以下样式:
| 参数 | 样式 |
|---|---|
| ‘-‘ | 实线 |
| ‘�C' | 虚线 |
| ‘-.' | 线-点 |
| ‘:' | 点虚线 |
linewidth参数指定折线的宽度,是个浮点数。
marker参数指定散点的样式,具体参照以下样式:
| 参数 | 样式 |
|---|---|
| ‘.' | 实心点 |
| ‘o' | 圆圈 |
| ‘,' | 一个像素点 |
| ‘x' | 叉号 |
| ‘+' | 十字 |
| ‘*' | 星号 |
| ‘^' ‘v' ‘<' ‘>' | 三角形(上下左右) |
| ‘1' ‘2' ‘3' ‘4' | 三叉号(上下左右) |
markerfacecolor参数指定marker的颜色
markersize参数指定marker的大小
这样就基本上能够自定义任何的折线图、散点图的样式了。
移动轴线
这段有点小复杂,暂时不想具体了解奇奇怪怪的函数调用,姑且先记录下用法和原理:
ax = gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
我们知道一张图有上下左右四个轴线,这里我们把右边和上边的轴线颜色调为透明,然后把下边设置到y轴数据为0的地方,把左边设置到x轴数据为0的地方。这样我们就能根据自己想要位置来调节轴线了。
比如下面这段官方的代码:
# -----------------------------------------------------------------------------
# Copyright (c) 2015, Nicolas P. Rougier. All Rights Reserved.
# Distributed under the (new) BSD License. See LICENSE.txt for more info.
# -----------------------------------------------------------------------------
import numpy as np
import matplotlib.pyplot as plt
plt.figure(figsize=(8,5), dpi=80)
ax = plt.subplot(111)
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)
plt.plot(X, C, color="blue", linewidth=2.5, linestyle="-")
plt.plot(X, S, color="red", linewidth=2.5, linestyle="-")
plt.xlim(X.min()*1.1, X.max()*1.1)
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
[r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])
plt.ylim(C.min()*1.1,C.max()*1.1)
plt.yticks([-1, 0, +1],
[r'$-1$', r'$0$', r'$+1$'])
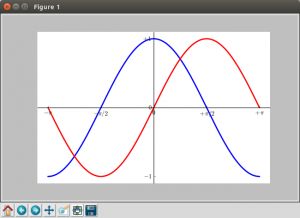
plt.show()
显示的结果就是:
图例和注解
图例十分简单,下述代码就可以解决:
plot(X, C, color="blue", linewidth=2.5, linestyle="-", label="cosine") plot(X, S, color="red", linewidth=2.5, linestyle="-", label="sine") legend(loc='upper left')
在plot里指定label属性就好了,最后调用下legend函数来确定图例的位置,一般就是'upper left'就好了。
注解就有点麻烦了,要用到annotate命令,挺复杂的,暂时是在不想看,姑且贴一段完整的代码和效果图吧:
# -----------------------------------------------------------------------------
# Copyright (c) 2015, Nicolas P. Rougier. All Rights Reserved.
# Distributed under the (new) BSD License. See LICENSE.txt for more info.
# -----------------------------------------------------------------------------
import numpy as np
import matplotlib.pyplot as plt
plt.figure(figsize=(8,5), dpi=80)
ax = plt.subplot(111)
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
X = np.linspace(-np.pi, np.pi, 256,endpoint=True)
C,S = np.cos(X), np.sin(X)
plt.plot(X, C, color="blue", linewidth=2.5, linestyle="-", label="cosine")
plt.plot(X, S, color="red", linewidth=2.5, linestyle="-", label="sine")
plt.xlim(X.min()*1.1, X.max()*1.1)
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
[r'$-\pi$', r'$-\pi/2$', r'$0$', r'$+\pi/2$', r'$+\pi$'])
plt.ylim(C.min()*1.1,C.max()*1.1)
plt.yticks([-1, +1],
[r'$-1$', r'$+1$'])
t = 2*np.pi/3
plt.plot([t,t],[0,np.cos(t)],
color ='blue', linewidth=1.5, linestyle="--")
plt.scatter([t,],[np.cos(t),], 50, color ='blue')
plt.annotate(r'$\sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$',
xy=(t, np.sin(t)), xycoords='data',
xytext=(+10, +30), textcoords='offset points', fontsize=16,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.plot([t,t],[0,np.sin(t)],
color ='red', linewidth=1.5, linestyle="--")
plt.scatter([t,],[np.sin(t),], 50, color ='red')
plt.annotate(r'$\cos(\frac{2\pi}{3})=-\frac{1}{2}$',
xy=(t, np.cos(t)), xycoords='data',
xytext=(-90, -50), textcoords='offset points', fontsize=16,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.legend(loc='upper left', frameon=False)
plt.savefig("../figures/exercice_9.png",dpi=72)
plt.show()
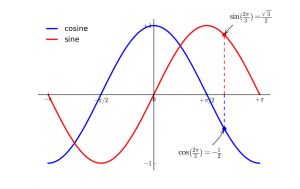
效果图:
还是十分高能的。。。
总结
以上就是这篇文章的全部内容了,希望本文的内容对大家学习或者使用python能带来一定的帮助,如果有疑问大家可以留言交流,谢谢大家对脚本之家的支持。