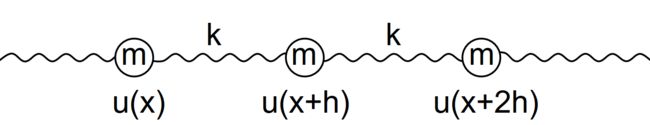Name: 贺一珺
Student Number: 2014302290002
Question
- 6.12 Gaussian initial starting displacements are convenient for the calculations of this section, but are not very realistic. When a real string, such as a guitar string, is plucked, the iniial string displacement is more accurately described by two straight lines that start at the ends of the string and end at the excitation point, as illustrated in Figure 6.4. Compare the power spectrum for a string excited in this manner with the results found above for a Gaussian initial wavepacket.
- 6.16 Perform the calculations described in this section.
Abstract
In last chapter we studied the numerical solution of Laplace equation and, participately, I solved the equation under several various boundary conditions. In this chapter I will try to study the wave motion, whose equation could generally be expressed as:
This equation can be derived from the model of a short segment of string forced by its neighberhood segments:
In this homework I will consider the solution of this equation under several different initial conditions, which is like what we did in last chapter. What's more, I will also analyse the composition of some wave equations, which is actually decomposed them into a number of various harmonic wave equations.
Background
Sound can propagate through a medium such as air, water and solids as longitudinal waves and also as a transverse wave in solids (see Longitudinal and transverse waves, below). The sound waves are generated by a sound source, such as the vibrating diaphragm of a stereo speaker. The sound source creates vibrations in the surrounding medium. As the source continues to vibrate the medium, the vibrations propagate away from the source at the speed of sound, thus forming the sound wave. At a fixed distance from the source, the pressure, velocity, and displacement of the medium vary in time. At an instant in time, the pressure, velocity, and displacement vary in space. Note that the particles of the medium do not travel with the sound wave. This is intuitively obvious for a solid, and the same is true for liquids and gases (that is, the vibrations of particles in the gas or liquid transport the vibrations, while the average position of the particles over time does not change). During propagation, waves can be reflected, refracted, or attenuated by the medium.
The behavior of sound propagation is generally affected by three things:
A complex relationship between the density and pressure of the medium. This relationship, affected by temperature, determines the speed of sound within the medium.
Motion of the medium itself. If the medium is moving, this movement may increase or decrease the absolute speed of the sound wave depending on the direction of the movement. For example, sound moving through wind will have its speed of propagation increased by the speed of the wind if the sound and wind are moving in the same direction. If the sound and wind are moving in opposite directions, the speed of the sound wave will be decreased by the speed of the wind.
The viscosity of the medium. Medium viscosity determines the rate at which sound is attenuated. For many media, such as air or water, attenuation due to viscosity is negligible.
When sound is moving through a medium that does not have constant physical properties, it may be refracted (either dispersed or focused).
Fourier Analysis
In mathematics, Fourier analysis is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer.
Today, the subject of Fourier analysis encompasses a vast spectrum of mathematics. In the sciences and engineering, the process of decomposing a function into oscillatory components is often called Fourier analysis, while the operation of rebuilding the function from these pieces is known as Fourier synthesis. For example, determining what component frequencies are present in a musical note would involve computing the Fourier transform of a sampled musical note. One could then re-synthesize the same sound by including the frequency components as revealed in the Fourier analysis. In mathematics, the term Fourier analysis often refers to the study of both operations.
The decomposition process itself is called a Fourier transformation. Its output, the Fourier transform, is often given a more specific name, which depends on the domain and other properties of the function being transformed. Moreover, the original concept of Fourier analysis has been extended over time to apply to more and more abstract and general situations, and the general field is often known as harmonic analysis. Each transform used for analysis (see list of Fourier-related transforms) has a corresponding inverse transform that can be used for synthesis.
Plotting
- Before the beginning
Here is the code
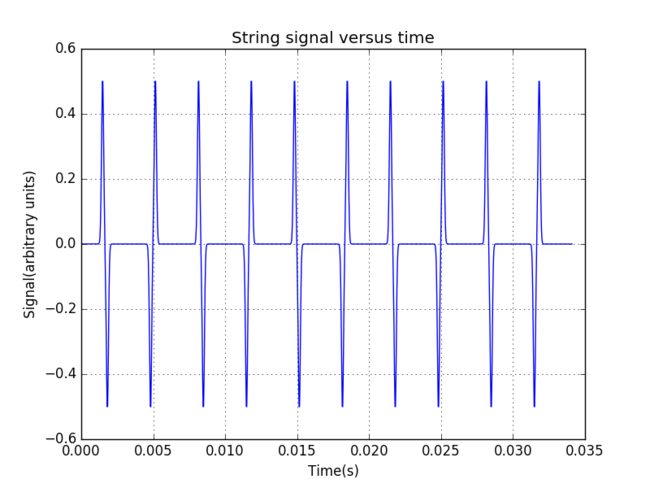
When we give the string a Gaussian purtrebution at the middle point of the string, the point 5% total wavelength from the boundary has the following motion:
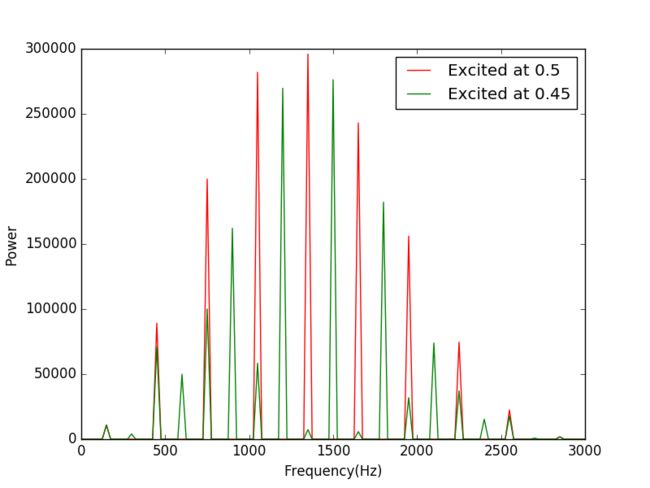
Its spectrum is:
- 6.12
Here is the code
When the upper point of triangle is in the middle of string:
The spectrum is:
When the upper point is not in the middle of string:
The spectrum is:
- 6.16
The frequency is
Acknowledgement
- Prof. Cai
- Yuqiao Wu
- wikipedia
How to contact me?
- Wechat ID: bestsola
- E-mail: [email protected]