简介
Python中对序列类型某个子集或者区间的检索称作切片。实际上,切片功能非常强大,能够提供对可编辑序列类型数据的增、删、改、查等各种操作,运用恰当的话会极大地节省编码量。因此,切片知识在Python开发中极其重要,如果啃不掉这根硬骨头,将会给你未来的Python开发之路带来极大挫败感。
全国二级Python考试中考查的序列类型主要有三种,即字符串、元组和列表,也是实战中使用最频繁的数据结构。其中,列表是可编辑的,而字符串和元组仅提供读操作。本文将以列表为例,详细介绍各种Python考级及实战中需要的切片取值技巧及有关注意事项。
1. 基础引例
我们假设读者是经过初步的切片学习在遇到技巧及概念障碍时才阅读此文的。为此,可以通过一个基本类型例子,引出切片涉及的基本概念,进而有助于更形象地理解切片。本部分中,如果尚存在疑问,请暂时保留,待认真阅读完全文后,应该能得到圆满解答。
直接创建列表 [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]:
a = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
a
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
切片的目的是把上述列表中符合某个规律(如等差数列、等比数列或者更复杂的规律)的元素组成的子集取出来。例如:
a
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
a[1:5:2]
[1, 3]
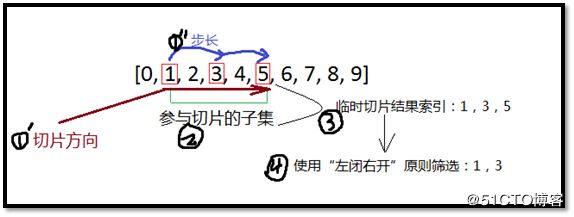
【简析】上述切片中,1为切片的起始索引,5为切片的结束索引,2为切片的步长。步长为2决定了切片的方向是从左向右。从索引1(包括)开始向索引5沿着从左向右顺序切(根据步长为2的规律)出符合条件的下标元素,仅有两个,即:a[1],a[3]。那么,a[5]是不是包含在结果中呢?不是。因为在确定符合条件的切片子集时,还有一个限定条件是:左闭右开。即对于上面的索引,应当是:[1,5)。请参考下图:
上面的引例中出现如下概念及问题:
【概念】步长(符号与大小)、切片的起始索引位置、切片的终止索引位置、切片的方向。
【问题】
如何确定参与切片的子集?
从哪个索引开始沿着什么方向以多大的跨度(步长)切片?切片的结束索引是什么?
当切片的起始索引位置与终止索引位置为空时如何处理?2. 切片语法格式
Sequence[start: end: step]
现总结切片规则如下:
- step:切片的跨度,也就是切片跳跃的长度,也称“步长”,默认值(省略时)为1。要求:必须是除零外的整数(可正可负)
- step为正时,则从左向右切片,如果start(可为0)和end同符号且start > end,则切片结果集一定为空
- step为负时,则从右向左切片,如果start(可为0)和end同符号且start < end,则切片结果集一定为空
- start:代表切片的起始索引位置。为空时,表示切片起始索引位置是整个列表的最开始(而且,结果集中包括该元素)。注意:这里的“最开始”并不等于“最左边”。
4.1当step为正,start对应列表的最左边(包含)。
4.2当step为负,start对应列表的最右边(=len(列表))。 - end:代表切片的截至索引位置。为空时,表示切片终止索引位置是整个列表的最后一个(切片到该元素结束,至于结果集中是否包括该元素,取决于step)。注意:这里的“最后一个”并不等于“最右边”。
5.1当step为正,end对应列表的最右边(=len(列表))。
5.2当step为负,end对应列表的最左边(包含)。 - start和end同时为空的时候,表示序列中所有元素都要参与切片。当step绝对值为1时,切片结果中包含序列中所有元素;当step绝对值大于1时,切片结果将按step值对应的切片规律包含序列中相应元素。
- 切片的时候,不存在索引越界的问题。例如,给定切片索引小于切片最小索引值,则截止到列表最左边;如果给定切片索引大于切片最大索引值,则截止到列表最右边。
【注意】步长值为0导致错误提示“ValueError: slice step cannot be zero”。
3. 正索引和负索引与等价项
实质上,序列类型提供了两种索引类型:正索引和负索引。还是以上面提到的列表a = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]为例,请各位观察下图。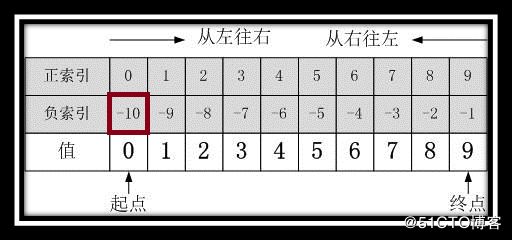
从图中看出:
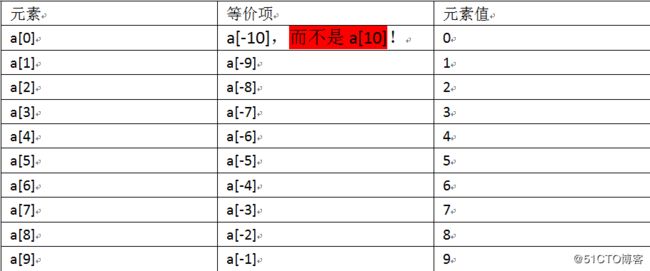
显然,存在这样的绝对值关系:
|0|+|-10|=10,|1|+|-9|=10,……|9|+|-1|=10
重要技巧
从上面看到,每一个列表(各种序列类型)中的元素都有两种下标(注意:a[0]对应a[-10])。在切片分析中,可以把下标转换成对应的下标来分析。如:
a[-6::2]等价于a[4::2]
a[:-6:-1] 等价于a[:4:-1]
a[-5:-2:2] 等价于a[5:8:2]
a[:2] 等价于a[0:2] 等价于a[0:2:1]
a[2:] 等价于a[2:10] 等价于a[2:10:1]
a[:2:] 等价于a[0:2] 等价于 a[0:2:1]
★a[::-1]等价于a[-1:-11:-1]
4. 典型切片取值举例
下面所有例子还是基于前面的列表:
a
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
为方便总结,我们来分小类型举例切片的应用。4.1. 切片表达式中仅有一对冒号情形
【提示】这种情况下,暗含着一个前提是:步长值step取值为1,因此切片方向遵循“自左向右”切的原则。
a
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]4.1.1 最简单情形
a[2:6]
[2, 3, 4, 5]
a[2:9]
[2, 3, 4, 5, 6, 7, 8]
【提示】在此两例中,符合“左闭右开”原则,故最后切片结果集中去掉最后一个下标元素。4.1.2 切片截止索引位置“超界”
根据上面切片规则7的说明,切片操作时索引不存在真正“越界”问题。请结合切片规则7看下面的举例。
a[2:10]
[2, 3, 4, 5, 6, 7, 8, 9]
【解析】根据“左闭右开”原则,切片结果集将包含a[2],a[3]……直到a[9]的8个元素。
a[2:20]
[2, 3, 4, 5, 6, 7, 8, 9]
【解析】根据切片规则7,a[2:20]等价于a[2:10](10=len(a),即列表最右边)。下面两个例子理由同这两个例子:
a[-3:10]
[7, 8, 9]
a[-3:20]
[7, 8, 9]4.1.3 切片的起始索引位置超界
a[-10:-8]
[0, 1]
a[-100:-8]
[0, 1]
a[-100:2]
[0, 1]
a[-10:2]
[0, 1]
【解析】根据切片规则7,a[-100:-8]等价于a[-10:-8],a[-10:2] 等价于a[-100:2]。另一方面,a[-10:-8] 等价于a[0:-8](等价于a[0:2]),a[-10:2] 等价于a[0:2],故有上面运行结果。4.1.4 切片起始索引或截止索引为负
a[-2:6]
[]
【解析】a[-2:6]等价于a[8:6],也等价于a[-2:6:1]和a[8:6:1],此时step=1(省略),易知切片结果集为空。
a[6:-2]
[6, 7]
【解析】a[6:-2]等价于a[6:8],也等价于a[6:-2:1]和a[6:8:1],此时step=1(省略),结合“左闭右开”原则,易知结果集对应[a[6],a[7]](而不包含a[8]),即切片结果集为[6, 7]。4.1.5 切片规则2应用
a[6:2]
[]
a[-2:-6]
[]
【解析】符合切片规则2,易知切片结果集为空。
a[-6:-2]
[4, 5, 6, 7]
【解析】a[-6:-2] 等价于a[4:8],结合“左闭右开”原则,易知结果集对应[a[4],a[5],a[6],a[7]](而不包含a[8]),即切片结果集为[4,5,6, 7]。4.1.6 省略切片起始索引时
a[:4]
[0, 1, 2, 3]
a[:-4]
[0, 1, 2, 3, 4, 5]
【解析】根据上面切片规则4.1,a[:4]等价于a[0:4],a[:-4] 等价于a[0:-4],而a[0:-4]又等价于a[0:6] ,结合“左闭右开”原则,易知有上面的切片结果集。4.1.7 省略切片截止索引时
a[4:]
[4, 5, 6, 7, 8, 9]
a[-4:]
[6, 7, 8, 9]
【解析】根据上面切片规则5.1,a[4:]等价于a[4:10] (10=len(a)),a[-4:]等价于a[6:],而a[6:]等价于a[6:10] (10=len(a)),结合切片规则6“左闭右闭”原则(a[9]包含在结果集中),易知有上面的切片结果集。4.1.8 切片起始索引和截止索引均省略时
a[:]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
【解析】根据上面切片规则4.1和5.1,a[:]等价于a[0:10](10=len(a)),而根据“左闭右开”原则,结果集中应当包含a[0],a[1],……a[9],故有上述切片结果集。4.2. 切片表达式中有两对冒号情形
在切片表达式有两对冒号情况下,当step为1时(因为这种情况下可以省略第二对冒号,所以对应上面仅有一对冒号时),绝大部分情形我们已经讨论过。
【前提】本部分中,我们还是使用与上面同样结构与内容的列表a,如下所示:
a=[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]4.2.1 step>1时
不失一般性,以下讨论不妨假设step=2。先看下面的例子。
a[2:7:2]
[2, 4, 6]
a[:3:2]
[0, 2]
a[:-3:2]
[0, 2, 4, 6]
a[3::2]
[3, 5, 7, 9]
a[-3::2]
[7, 9]
【解析】首先注意到,step=2决定了切片方向是自左向右。当step>1时,切片起始索引值默认为0。对于负数形式的起始还是截止索引值都可以转换成等价的正数形式索引值(例如a[:-3:2]等价于a[:7:2]),a[-3::2] 等价于a[7::2])来分析的。再结合“左闭右开”原则,这一组例题应该不难理解,故细节的解释在此省略。4.2.2 step为负整数时
例1
a[8:3:-1]
[8, 7, 6, 5, 4]
【解析】首先注意到,step为-1决定了切片方向是自右向左。本例中,切片起始索引为8,终止索引为3,再结合切片“左闭右开”原则,故切片结果集中元素有[a[8],a[7],a[6],a[5],a[4]],即[8,7,6,5,4]。例2
a[10:0:-2]
[9, 7, 5, 3, 1]
【解析】首先注意到,step为-2决定了切片方向是自右向左。其次,根据上面切片原则7,切片的时候不存在索引越界情况,a[10]不存在,则继续往内分析,a[9]=9。于是,结合切片“左闭右开”原则和步长(即跨度)为2,故切片结果集中元素有[a[9],a[7],a[5],a[3],a[1]],即[9,7,5,3,1]。例3
a[0:10:-2]
[]
【解析】首先注意到,step为-2决定了切片方向是自右向左。而切片初始索引为0,即列表的左边界,此时再向左切肯定没有元素可切了。因此,根据切片规则3,结果为空列表。例4
a[:4:-1]
[9, 8, 7, 6, 5]
【解析】首先注意到,step为-1决定了切片方向是自右向左。此时,切片初始索引对应列表的最右边(=len(列表)),即有切片从索引10(实际从索引9开始,包含该索引)开始沿着自右向左的方向切片,直到索引4(不包含,依据是“左闭右开”),故有上述切片结果。例5
a[::-1]
[9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
【解析】首先注意到,step为-1决定了切片方向是自右向左。那么,接下来最关键的问题是搞清:在step为负数且切片初始索引和切片终止索引没有提供的情况下,这个切片初始索引和切片终止索引的值为多少。结合上面规则4.2和5.2,初始索引对应列表的最右边(=len(列表)),切片的截至索引位置为列表的最左边的左侧(即参与切片的子集中包含索引为0的元素)。当然,也可以简单根据上面规则6确定出最终的切片结果为列表中原来所有元素的倒序。例6
a[5::-2]
[5, 3, 1]
【解析】首先注意到,step为-2决定了切片方向是自右向左。切片初始索引为5,结果集中自然包含a[5]。根据上面分析,本例中切片的截至索引位置为列表的最左边的左侧(即参与切片的子集中包含索引为0的元素)。从等价关系来分析的话,a[5::-2]等价于a[5:-11:-2](下标-11对应着下标-10再往左,类似于下标9再往右对应的下标10)。所以,有此例中运行结果。思考题
a[0::-1]的结果是多少?
a[:-3:2] 的结果是多少?
a[1:6:-1] 的结果是多少?
a[-6::-1] 的结果是多少?
连续切片操作:a[:8][2:5][-1:] 的结果是多少?
a[2+1:3*2:7%3] 的结果是多少?
下列代码片断的运行结果是什么?
for i in range(1,100)[2::3][-10:]:
print(i)
【提示】利用range函数生成1-99的整数,然后取3的倍数,再取最后十个。小结
理论上而言,只要条件表达式得当,可以通过单次或多次切片操作实现任意切取目标值。初看上去,切片操作的基本语法比较简单,但是深挖起来,并不简单。因此,如果不彻底搞清楚内在逻辑,也极容易产生错误,而且这种错误有时隐蔽得比较深,难以察觉。
作为补充,本文中提到的“左闭右开”原则,更细致地说法是“开始闭结束开”原则。即是说,开始索引对应元素参与切片运算,而结束索引对应元素并不参与切片运算。另外,步长值为负数,并且在省略切片起始索引或者切片终止索引情况下,这两种索引的默认值应当结合“切片不存在索引越界”原则进行正确理解。本文通过详细例子总结归纳了切片操作的各种情况。若有错误和不足之处请各位指正!