1.算法
1.1时间复杂度
时间复杂度:用来评估算法运行效率的一个式子!

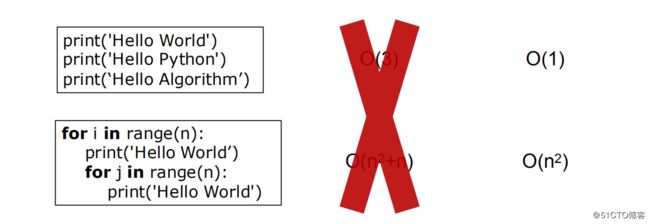
由于print()一次与print多次,执行时间相差很小,所以时间复杂度统一为O(1)。
相对于循环来说,中间执行的代码时间相对来说很小,所以只要是循环,时间复杂度只与循环的次数有关。

小节:
1.时间复杂度是用来估计算法运行时间的一个式子。
2.一般来说,时间复杂度高的算法比复杂度低的算法慢。
3.常见的时间复杂度效率
O(1)
快速判断算法复杂度规模(适用于大多数情况):
1.没有循环,为O(1)
2.循环n次,为O(n)
3.k层循环,为n^k
4.循环减半,为log2^n
复杂情况,根据算法执行过程判断
1.2空间复杂度
空间复杂度:用来评估算法内存占用大小的式子。
1.算法只是使用了一些变量,空间复杂度为O(1)。
2.算法使用了长度为n的一维列表,空间复杂度为O(n)。
3.算法使用了m行n列的二维列表,空间复杂度为O(m*n)
在实际编程中,我们都会以空间来换取时间,即使占用内存,也要争取速度。
2.递归
2.1常见例子

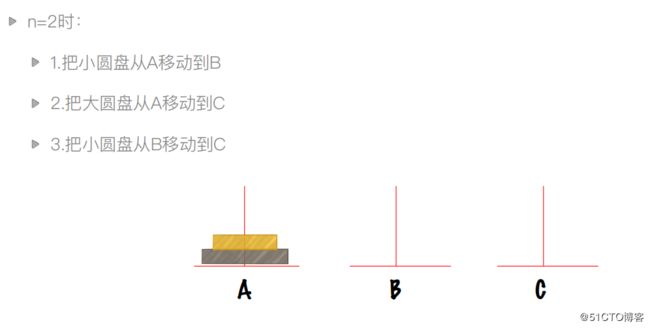
2.2汉诺塔问题
要求把所有圆盘从A上挪到另一个柱子上
小圆盘不能放在大圆盘上
一次只能移动一个盘子

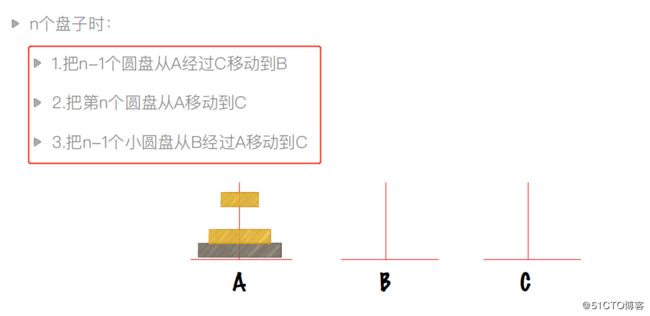
#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author: vita
def hanio(n,a,b,c):
if n>0:
hanio(n-1,a,c,b)
print("from %s to %s"%(a,c))
hanio(n-1,b,a,c)
hanio(3,"A", "B", "C")
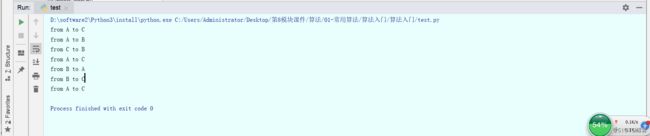
汉诺塔移动次数的递推式:h(x)=2h(x-1)+1
2.列表查找
2.1顺序查找
顺序查找:也叫线性查找,从列表第一个元素开始,顺序搜索,直到找到元素或搜索到最后一个元素。
时间复杂度为O(n)
#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author: vita
def search(li,val):
for index, v in enumerate(li):
if v == val:
return index
return None
index = search([1,2,4,5,9,3], 4)
print(index) # 2
2.2二分法查找
⼆分查找:⼜叫折半查找,从有序列表的初始候选区li[0:n]开
始,通过对待查找的值与候选区中间值的⽐较,可以使候选
区减少⼀半。
时间复杂度:O(logn)

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author: vita
def search(li,val):
length = len(li)
min = 0
max = length - 1
while min <= max:
mid = (min + max)//2
if li[mid] == val:
return mid
elif li[mid] > val:
max = mid -1
elif li[mid] < val:
min = mid + 1
return None
index = search([1,2,4,5,9], 4)
print(index) # 2
3.列表排序
排序:将一组"无序"的列表调整为"有序"列表
有升序与降序排列
python内置排序函数:sort()

3.1冒泡排序
列表每相邻的数,如果前面比后面的大,则交换这两个数。
一趟排序完成后,最后一个是最大的,无序区域减少一个数。有序区域增加一个数。
时间复杂度为O(n^2)
def bubble(li):
for i in range(len(li)-1):
for j in range(len(li)-i-1):
if li[j]>li[j+1]:
li[j],li[j+1]=li[j+1],li[j]
print(li)
return li
res = bubble([2,4,5,1,7,6])
print(res)

冒泡排序优化:
如果冒泡排序中的一趟排序没有发生交还,则说明列表已经有序,可以直接结束算法。
def bubble(li):
for i in range(len(li)-1):
exchange = False
for j in range(len(li)-i-1):
if li[j]>li[j+1]:
li[j],li[j+1]=li[j+1],li[j]
exchange = True
print("----------",li)
if not exchange:
break
return li
res = bubble([1,2,3,4,5,6])
print(res)
3.2选择排序
一趟排序记录最小的数,放在第一个位置。
再一次排序记录无序区最小的数,放到第二个位置。
算法关键点:有序区和无序区,无序区最小数的位置。
时间复杂度:O(n^2)
def select(li):
for i in range(len(li)-1):
min_index = i
for j in range(i+1, len(li)):
if li[j]

3.3插入排序
时间复杂度为O(n^2)


def insert(li):
for i in range(1,len(li)):
tmp = li[i] # 这是拿到的牌
j = i - 1 # 这是手里的牌
while j>=0 and tmp















