using suduku_4.txt as an example
bare_tex_output()
this is an easy one, only convert suduku_4.txt to tex file.
forced_tex_output()
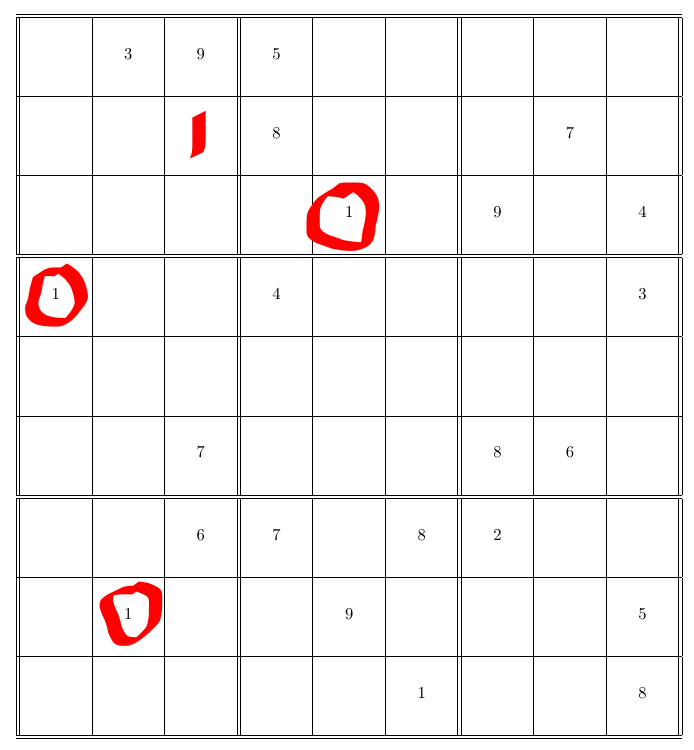
look at box 1 first:
- c(4, 1) force that 1 can not be in row 1
- c(8, 2) force that 1 can not be in row 2
- c(3, 5) force that 1 can not be in column 3
therefore, in box 1, 1 only can be in c(2, 3)
similarly, we can fill 9 in c(2, 6)
marked_tex_output()
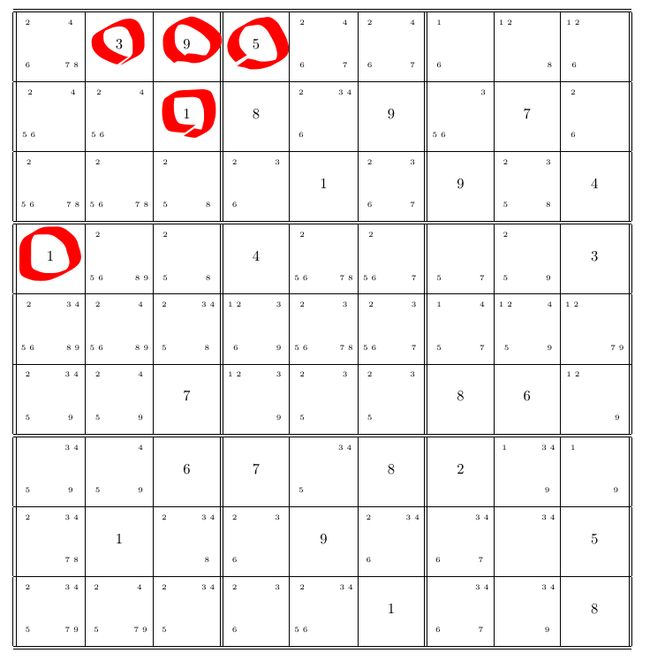
this is quite straightforward, taking c(1,1) for example.
- column 1: 3, 9, 5
- row 1: 1
- box 1: 1, 3, 9
therefore , c(1,1) can only be fill with numbers other than (1, 3, 5, 9), which are (2, 4, 6, 7, 8)
worded_tex_output()
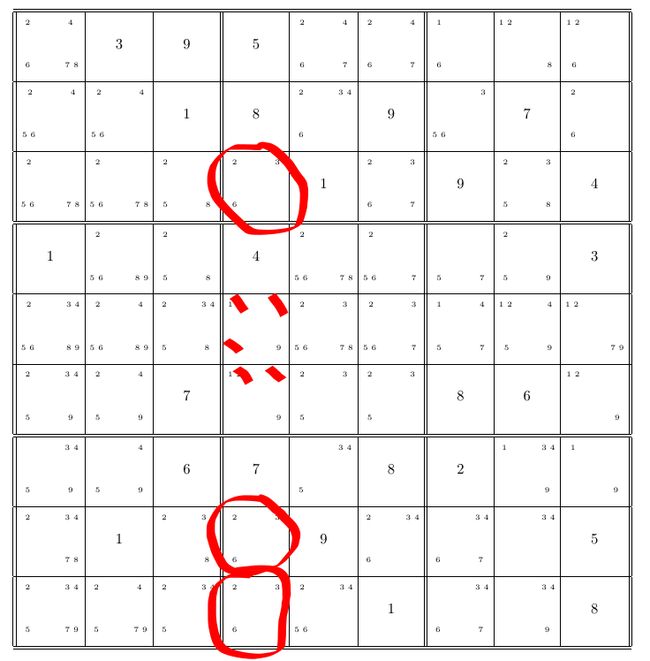
1. we can find preemptive set in column:
- there are 3 cells, calculate their union: c(3, 4) U c(8, 4) U c(9, 4) = (2, 3, 6)
- the number of integers in set (2, 3, 6) is 3, which is equal to the number of cells
therefore, c(3, 4), c(8, 4) , c(9, 4) is a preemptive set
we can cross (2, 3, 6) in other cells in column 4
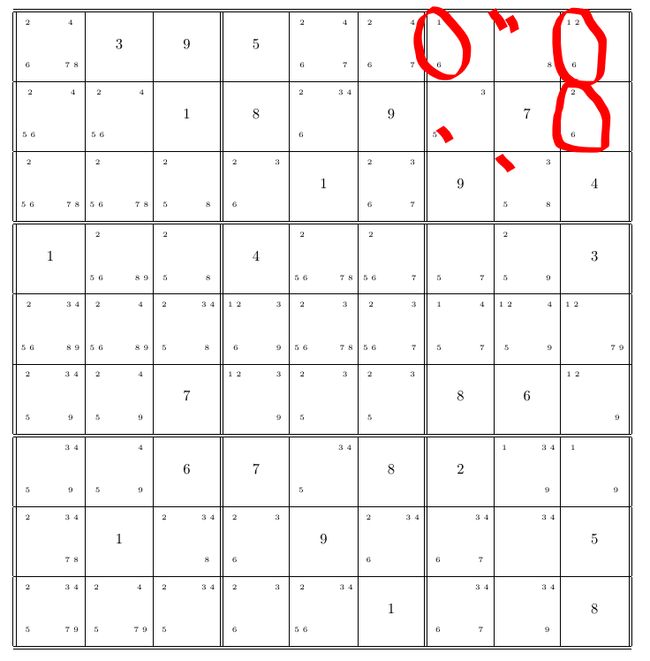
2. we can find preemptive set in box:
- there are 3 cells in box 3, calculate their union: c(1, 7) U c(9, 1) U c(9, 2) = (1, 2, 6)
- the number of integers in set (1, 2, 6) is 3, which is equal to the number of cells
therefore, c(1, 7), c(9, 1) , c(9, 2) is a preemptive set
we can cross (1, 2, 6) in other cells in box 3
3. we can find preemptive set in row:
which is similar to finding preemptive set in column and box
4. combine with other method:
Every time after we use preemptive set to change the table, we should use the methods which described in forced_tex_output() and marked_tex_output() again.
After that, we should try to find preemptive again, until nothing need to be changed.
All preemptive set in sudoku_3:
there is no preemptive set in sudoku_3
All preemptive set in sudoku_4:
which may different depend on your algrithm
preemptive set: {2, 3, 6} on column 4 , [[9, 4], [3, 4], [8, 4]]
preemptive set: {1, 2, 6, 9} on column 9 , [[1, 9], [2, 9], [6, 9], [7, 9]]
preemptive set: {1, 2, 6} on box 3 , [[1, 7], [2, 9], [1, 9]]
preemptive set: {1, 9} on box 5 , [[5, 4], [6, 4]]
preemptive set: {2, 3, 5, 6, 7, 8} on box 5 , [[6, 5], [6, 6], [5, 6], [5, 5], [4, 5], [4, 6]]
preemptive set: {1, 3, 4, 9} on box 9 , [[7, 8], [7, 9], [8, 8], [9, 8]]
preemptive set: {6, 7} on column 7 , [[9, 7], [8, 7]]
preemptive set: {1, 9} on box 5 , [[5, 4], [6, 4]]
preemptive set: {2, 3, 5, 6, 7, 8} on box 5 , [[6, 5], [6, 6], [5, 6], [5, 5], [4, 5], [4, 6]]
preemptive set: {6, 7} on box 9 , [[9, 7], [8, 7]]
preemptive set: {1, 3, 4, 9} on box 9 , [[7, 8], [7, 9], [8, 8], [9, 8]]
preemptive set: {8, 2} on column 3 , [[3, 3], [4, 3]]
preemptive set: {3, 4, 5} on column 3 , [[5, 3], [8, 3], [9, 3]]
preemptive set: {1, 9} on column 4 , [[5, 4], [6, 4]]
preemptive set: {2, 3, 6} on column 4 , [[3, 4], [8, 4], [9, 4]]
preemptive set: {2, 6} on column 9 , [[1, 9], [2, 9]]
preemptive set: {1, 9} on box 5 , [[5, 4], [6, 4]]
preemptive set: {2, 3, 5, 6, 7, 8} on box 5 , [[6, 5], [6, 6], [5, 6], [5, 5], [4, 5], [4, 6]]
preemptive set: {3, 4, 5, 9} on box 7 , [[7, 2], [9, 3], [7, 1], [8, 3]]
preemptive set: {2, 3, 4, 5, 7, 9} on box 7 , [[9, 3], [9, 2], [7, 2], [9, 1], [7, 1], [8, 3]]
preemptive set: {6, 7} on box 9 , [[9, 7], [8, 7]]
preemptive set: {1, 3, 4, 9} on box 9 , [[7, 8], [7, 9], [8, 8], [9, 8]]
preemptive set: {1, 9} on row 6 , [[6, 9], [6, 4]]
preemptive set: {2, 3, 4, 5} on row 6 , [[6, 1], [6, 2], [6, 5], [6, 6]]
preemptive set: {3, 4} on row 8 , [[8, 3], [8, 8]]
preemptive set: {2, 6, 7} on row 8 , [[8, 4], [8, 6], [8, 7]]
preemptive set: {2, 3, 4, 6} on row 8 , [[8, 3], [8, 4], [8, 6], [8, 8]]
preemptive set: {2, 7} on row 9 , [[9, 1], [9, 2]]
preemptive set: {8, 2} on column 3 , [[3, 3], [4, 3]]
preemptive set: {3, 4, 5} on column 3 , [[5, 3], [8, 3], [9, 3]]
preemptive set: {1, 9} on column 4 , [[5, 4], [6, 4]]
preemptive set: {2, 3, 5, 6, 7} on column 6 , [[3, 6], [4, 6], [5, 6], [6, 6], [8, 6]]
preemptive set: {2, 6} on column 9 , [[1, 9], [2, 9]]
preemptive set: {1, 9} on column 9 , [[6, 9], [7, 9]]
preemptive set: {2, 6, 7, 8} on box 1 , [[1, 1], [3, 2], [3, 1], [3, 3]]
preemptive set: {2, 6} on box 2 , [[3, 4], [2, 5]]
preemptive set: {1, 9} on box 5 , [[5, 4], [6, 4]]
preemptive set: {2, 3, 5, 6, 7, 8} on box 5 , [[6, 5], [6, 6], [5, 6], [5, 5], [4, 5], [4, 6]]
preemptive set: {2, 7} on box 7 , [[9, 2], [9, 1]]
preemptive set: {3, 4, 5, 9} on box 7 , [[9, 3], [7, 2], [7, 1], [8, 3]]
preemptive set: {4, 5} on box 8 , [[7, 5], [9, 5]]
preemptive set: {2, 6} on box 8 , [[8, 6], [8, 4]]
preemptive set: {2, 6, 8, 9} on row 4 , [[4, 2], [4, 3], [4, 5], [4, 8]]
preemptive set: {1, 9} on row 6 , [[6, 9], [6, 4]]
preemptive set: {2, 3, 4, 5} on row 6 , [[6, 1], [6, 2], [6, 5], [6, 6]]
preemptive set: {3, 4} on row 8 , [[8, 3], [8, 8]]
preemptive set: {2, 6} on row 8 , [[8, 4], [8, 6]]
preemptive set: {2, 7} on row 9 , [[9, 1], [9, 2]]
preemptive set: {4, 5} on row 9 , [[9, 3], [9, 5]]
preemptive set: {2, 4, 5, 7} on row 9 , [[9, 1], [9, 2], [9, 3], [9, 5]]
preemptive set: {2, 6, 7} on column 1 , [[1, 1], [3, 1], [9, 1]]
preemptive set: {3, 4, 5, 9} on column 1 , [[2, 1], [5, 1], [6, 1], [7, 1]]
preemptive set: {8, 2} on column 3 , [[3, 3], [4, 3]]
preemptive set: {3, 4, 5} on column 3 , [[5, 3], [8, 3], [9, 3]]
preemptive set: {2, 6} on column 4 , [[3, 4], [8, 4]]
preemptive set: {1, 9} on column 4 , [[5, 4], [6, 4]]
preemptive set: {4, 5} on column 5 , [[9, 5], [7, 5]]
preemptive set: {2, 3, 6, 8} on column 5 , [[2, 5], [4, 5], [5, 5], [6, 5]]
preemptive set: {2, 6} on column 9 , [[1, 9], [2, 9]]
preemptive set: {4, 5} on box 1 , [[2, 1], [2, 2]]
preemptive set: {2, 6, 7, 8} on box 1 , [[1, 1], [3, 2], [3, 1], [3, 3]]
preemptive set: {1, 9} on box 5 , [[5, 4], [6, 4]]
preemptive set: {2, 3, 5, 6, 8} on box 5 , [[6, 5], [6, 6], [5, 6], [5, 5], [4, 5]]
preemptive set: {2, 7} on box 7 , [[9, 2], [9, 1]]
preemptive set: {3, 4, 5, 9} on box 7 , [[9, 3], [7, 2], [7, 1], [8, 3]]
preemptive set: {4, 5} on box 8 , [[7, 5], [9, 5]]
preemptive set: {2, 6} on box 8 , [[8, 6], [8, 4]]
preemptive set: {3, 4, 5} on column 1 , [[2, 1], [5, 1], [6, 1]]
preemptive set: {4, 5} on column 5 , [[9, 5], [7, 5]]
preemptive set: {2, 5} on column 6 , [[5, 6], [6, 6]]
preemptive set: {4, 5} on box 1 , [[2, 1], [2, 2]]
preemptive set: {3, 5} on box 4 , [[5, 3], [5, 1]]
preemptive set: {2, 5} on box 5 , [[5, 6], [6, 6]]
preemptive set: {4, 5} on box 7 , [[9, 3], [7, 2]]
preemptive set: {2, 7} on box 7 , [[9, 2], [9, 1]]
preemptive set: {2, 4, 5, 7} on box 7 , [[9, 2], [7, 2], [9, 1], [9, 3]]
preemptive set: {4, 5} on row 7 , [[7, 2], [7, 5]]
preemptive set: {4, 5} on row 9 , [[9, 3], [9, 5]]
All preemptive set in sudoku_5:
preemptive set: {4, 7} on row 2 , [[2, 1], [2, 9]]
preemptive set: {2, 4, 9} on row 4 , [[4, 4], [4, 6], [4, 7]]