KKT(Karush-Kuhn-Tucher)条件

KKT(Karush-Kuhn-Tucher)条件

在优化理论中，KKT条件是非线性规划（nonlinear programming)最佳解的必要条件。KKT条件将lagrange乘数法（Lagrange multipliers）中的等式约束优化问题推广至不等式约束。本文从Lagrange乘数法推导KKT条件。

给定一个目标函数 f:Rn→R ，我们希望找到 x∈Rn ，在满足约束条件 g(x)=0 的前提下，使得 f(x) 有最小值。这个约束优化问题如下:

minimize f(x)
subject to g(x)=0

为方便分析，假设 f 对 g 是连续可导函数。Lagrange乘数法是含等式约束条件优化问题的典型解法。定义Lagrangian函数

L(x,λ)=f(x)+λg(x)

其中 λ 为Lagrange乘数。Lagrange乘数法将原来的约束优化问题转化成等价的非约束问题

minimize x,λL(x,λ)

优化必要条件：

▽xL=∂L∂x=▽f+λg(x)=0
▽λL=∂L∂λ=g(x)=0

其中第一个为stationary equation，第二个为约束条件。通过求解上述方程，可得 L(x,λ) 的驻点（stationary point） x∗ 以及 λ 的值（正负数皆可能）。

接下来我们将约束等式 g(x)=0 推广为 g(x)⩽0 。优化问题如下：

minimize f(x)
subject to g(x)⩽0

约束不等式 g(x)⩽0 称为primal feasibility， 由此定义可行域（feasible region） K={x∈Rn∣g(x)⩽0} 。假设 x∗ 为满足约束条件的最佳解，分两种情况讨论：（1） g(x∗)⩽0 ，最佳解位于 K 的内部，称为interior solution，这时约束条件是无效的；（2） g(x∗)=0 ，最佳解落在 K 的边界，称为boundary solution，此时约束条件是有效的。这两种情况的最佳解具有不同的必要条件。

• 内部解：在约束条件无效的情形下， g(x) 不起作用，约束优化问题退化为无约束优化问题，因此驻点 x∗ 满足 ▽f=0 且 λ=0 。
• 边界解：在约束条件有效的情形下，约束不等式变成等式 g(x)=0 ，这与前面Lagrange乘数法的情况相同。我们可以证明驻点 x∗ 发生在 ▽f∈span{▽g} ，换句话说，存在 λ 使得 ▽f=−λg(x) ，但这里 λ 的正负号是尤其意义的。因为我们希望最小化 f ，梯度 ▽f 应该指向可行域 K 的内部，但 ▽g 指向可行域 K 的外部（即 g(x)>0 的区域），因此 λ⩾0 称为对偶可行性
• 更直观的图解来自https://en.wikipedia.org/wiki/Karush%E2%80%93Kuhn%E2%80%93Tucker_conditions 及 http://blog.csdn.net/johnnyconstantine/article/details/46335763：
  
  

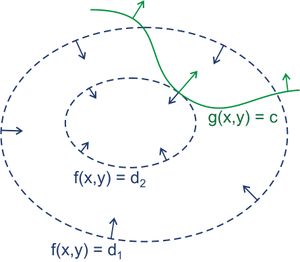
不论是内部解还是边界解， λg(x)=0 恒成立，称为complementary slckness。综上，最佳解的必要条件包括lagrangian函数 L(x,λ) 的定常方程式、原始可行性、对偶可行性，以及complementary slckness：

▽xL=▽f+λg(x)=0
g(x)⩽0
λ⩾0
λg(x)=0

以上就是KKT条件。如果我们要做大化 f(x) 且受限于 g(x)⩽0 ，那么对偶可行性要改成 λ⩽0

考虑标准约束优化问题

minimize f(x)
subject to g(x)=0 , j=1,...,m
　　　　　 hk(x)⩽0 , k=1,...,p

定义拉格朗日函数

L(x,{λj},{μk})=f(x)+∑mj=1λjgj(x)+∑pk=1μkhk(x)

其中 λj 是对应 gj(x)=0 的拉格朗日乘数， μk 是对应 hk(x)⩽0 的拉格朗日乘数，KKT条件

▽xL=0
gj=0,j=1,...,m
hk(x)⩽0
μk⩾0
μkhk(x)=0,k=1,...,p

**感谢**johnnyconstantine，ccjou