【牛客网】—— 2017年校招真题
前面几篇博客讲了2017年校招真题几个题的多种解法
删除公共字符串
倒置字符串
出现次数大于n/2的数
今天在这整理一下2017年校招真题中几个比较经典的题目，对解题思路进行详细的解析
题目ID：46579 - - 计算糖果
题目描述
A,B,C三个人是好朋友,每个人手里都有一些糖果,我们不知道他们每个人手上具体有多少个糖果,但是我们知道以下的信息：
A - B, B - C, A + B, B + C. 这四个数值.每个字母代表每个人所拥有的糖果数.
现在需要通过这四个数值计算出每个人手里有多少个糖果,即A,B,C。这里保证最多只有一组整数A,B,C满足所有题设条件。
输入描述:
输入为一行，一共4个整数，分别为A - B，B - C，A + B，B + C，用空格隔开。 范围均在-30到30之间(闭区间)。
输出描述:
输出为一行，如果存在满足的整数A，B，C则按顺序输出A，B，C，用空格隔开，行末无空格。 如果不存在这样的整数A，B，C，则输出No
示例1
输入： 1 -2 3 4
输出： 2 1 3
解题思路
这道题目的实质是：判断三元一次方程组是否有解及求解。
把题目条件用方程式表示：
A-B=Y1;
B-C=Y2;
A+B=Y3;
B+C=Y4;
用消元法求解：
A=(Y1+Y3)/2;
B=(Y3-Y1)/2=(Y2+Y4)/2;
C=(Y4-Y2)/2;
由于题目给出的是整数，要求解也是整数，这个约束条件也需要注意下。
不满足约束条件就是没解，就可以输出No了，满足所有的约束条件那就是有解。
代码实现
#include
using namespace std;
int main()
{
int a, b, c, d;
cin >> a >> b >> c >> d;
int A = (a + c) / 2;
int C = (d - b) / 2;
int B1 = (c - a) / 2;
int B2 = (b + d) / 2;
if (B1 != B2)
cout << "No";
else
cout << A << " " << B1 << " " << C;
return 0;
}
题目ID：58541-进制转换
题目描述
给定一个十进制数M，以及需要转换的进制数N。将十进制数M转化为N进制数
输入描述:
输入为一行，M(32位整数)、N(2 ≤ N ≤ 16)，以空格隔开。
输出描述:
为每个测试实例输出转换后的数，每个输出占一行。如果N大于9，则对应的数字规则参考16进制（比如，10用A表示，等等）
示例1
输入：7 2
输出：111
解题思路
- 这里思路就比较巧妙了，通过题目我们可以看到N(2 ≤ N ≤ 16)，说明必须支持2到16进制的转换，这里我们定义了一个对应字符的表table = “0123456789ABCDE”，通过十进制数M除以对应进制数N在table中的映射，找出对应的字符，相加到一起就是对应转换后的进制数,这里需要注意一下就是负数的处理，其实也很好理解，若M是负数，将他转换为整数，并输出一个负号，在进制转换数输出之前即可。举个栗子看看：
题目ID：45842 - - 统计回文
题目描述
“回文串”是一个正读和反读都一样的字符串，比如“level”或者“noon”等等就是回文串。花花非常喜欢这种拥有对称美的回文串，生日的时候她得到两个礼物分别是字符串A和字符串B。现在她非常好奇有没有办法将字符串B插入字符串A使产生的字符串是一个回文串。你接受花花的请求，帮助她寻找有多少种插入办法可以使新串是一个回文串。如果字符串B插入的位置不同就考虑为不一样的办法。
例如：
A = “aba”，B = “b”。这里有4种把B插入A的办法：
- 在A的第一个字母之前: “baba” 不是回文
- 在第一个字母‘a’之后: “abba” 是回文
- 在字母‘b’之后: “abba” 是回文
- 在第二个字母’a’之后 “abab” 不是回文
所以满足条件的答案为2
输入描述:
每组输入数据共两行。
第一行为字符串A
第二行为字符串B
字符串长度均小于100且只包含小写字母
输出描述:
输出一个数字，表示把字符串B插入字符串A之后构成一个回文串的方法数
示例1
输入：aba
：b
输出：2
解题思路
- 这道题的思路是这样的：使用暴力求解方式计算即可，遍历str1，将str2 insert进入str1的每个位置，判断是否是回文，是就++count；需要注意的是这里不能 str1.insert(i, str2)，这样的话str1改变了，判断下一个位置就不对了。所以每次使用str1拷贝构造一个str，然后str3.insert(i, str2)，再判断。
代码实现
#include
#include
using namespace std;
bool isPalindrome(string& str)
{
size_t begin = 0;
size_t end = str.size() - 1;
while (begin < end)
{
if (str[begin] == str[end])
{
++begin;
--end;
}
else
break;
}
if (begin < end)
return false;
else
return true;
}
int main()
{
int count = 0;
string str1, str2;
getline(cin, str1);
getline(cin, str2);
for (size_t i = 0; i <= str1.size(); ++i)
{
string str3 = str1;
str3.insert(i, str2);
if (isPalindrome(str3))
count++;
}
cout << count << endl;
return 0;
}
题目ID：58539-连续最大和
题目描述
一个数组有 N 个元素，求连续子数组的最大和。 例如：[-1,2,1]，和最大的连续子数组为[2,1]，其和为 3
输入描述:
输入为两行。 第一行一个整数n(1 <= n <= 100000)，表示一共有n个元素
第二行为n个数，即每个元素,每个整数都在32位int范围内。以空格分隔。
输出描述:
所有连续子数组中和最大的值。
示例1
输入：3 -1 2 1
输出：3
解题思路
- 这里用到了动态规划的思想，假设sum[i-1]是以数组中第nums[i-1]为最后一个元素的一段子数组最大和， sum[i]是以数组中第nums[i]为最后一个元素的一段子数组最大和，那么sum[i] = max(sum[i-1], 0) + nums[i]，理解了这个，下面代码中用sum1表示sum[i-1]，sum2表示sum[i]，如果计算出更大的子数组和则保存到result中。如果sum[i]，及sum2都小于0了，则置为0，因为他加上数组下一个数，不会计算出更大的子数组和。
代码实现
#include
#include
using namespace std;
int main()
{
int size;
cin >> size;
vector nums(size);
for (size_t i = 0; i < size; ++i)
cin >> nums[i];
int result = nums[0];
int sum1 = 0, sum2 = 0;
for (int i = 0; i < nums.size(); i++)
{
// 计算到num[i]的子数组的最大和
sum2 = sum1 >= 0 ? sum1 + nums[i] : nums[i];
if (sum2 > result)
result = sum2;
if (sum2 < 0)
sum2 = 0;
sum1 = sum2;
}
cout << result << endl;
return 0;
}
这里还有一个稍微简洁一些的代码，其实思路是相似的，但是更好理解一些
#include
using namespace std;
int main(){
int n,curSum = 0,maxSum = -1e5;
cin >> n;
int arr[n];
for(int i = 0;i < n;i++){
cin >> arr[i];
curSum += arr[i];
if(curSum > maxSum){
maxSum = curSum;
}
if(curSum < 0){
curSum = 0;
}
}
cout << maxSum << endl;
return 0;
}
题目ID：45840-不要二
题目描述
二货小易有一个W*H的网格盒子，网格的行编号为0H-1，网格的列编号为0W-1。每个格子至多可以放一块蛋糕，任意两块蛋糕的欧几里得距离不能等于2。
对于两个格子坐标(x1,y1),(x2,y2)的欧几里得距离为:( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) ) 的算术平方根,小易想知道最多可以放多少块蛋糕在网格盒子里。
输入描述:
每组数组包含网格长宽W,H，用空格分割.(1 ≤ W、H ≤ 1000)
输出描述:
输出一个最多可以放的蛋糕数
示例1
输入:3 2
输出:4
解题思路
解法一：
- 我们先来说一种很好理解的方法，但是代码稍微有点复杂，我们先来分析一下这个欧几里得距离的公式，我们可以发现其实他可以改写成（X1 - X2）的平方加上（Y1-Y2）的平方，不难发现其实就是两个位置之间的距离的平方
- 如果(x1,y1)放了蛋糕，则满足 ( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) ) == 4的(x2,y2)不能放蛋糕。
( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) ) == 4看起来是一个无解的表达式。
但是可以进行加法表达式分解：
1+3=4
3+1=4
2+2=4
0+4=4
4+0=4
但是我们知道放蛋糕的格子的位置肯定是整数，所以要么就是X1 - X2 = 2，要么就是Y1 - Y2 = 2，讲到这相信很多人就可以理解了。 - 那么我们不妨假设所有格子都可以放蛋糕，然后遍历这个二维数组(网格可以看做一个二维数组),如果某个位置能放蛋糕，遍历一个是1的位置，就++count，再计算出若是该位子能放蛋糕，哪些位置不能放，将不能放的位置置为0，最后输出count就是能放蛋糕的总数。
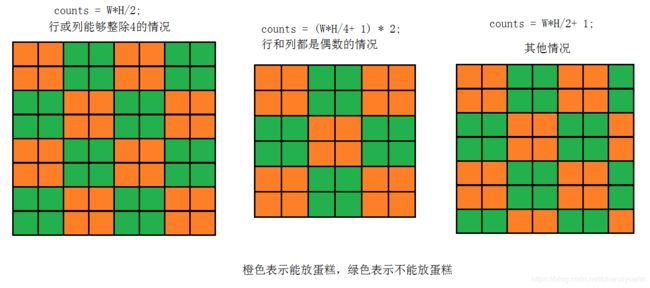
解法二：
- 这种解法相较前一种要更难理解一点，但是，代码实现起来要简单很多
- 我们将行和列分为以下三种情况来处理：
- 1.行能整除4,或者列能整除4
- 2.行和列都是偶数
- 3 其他情况可一并处理
代码实现
解法一
#include
#include
using namespace std;
int main()
{
int w, h, res = 0;
cin >> w >> h;
vector> a;
a.resize(w);
for (auto& e : a)
e.resize(h, 1);
for (int i = 0; i 解法二
#include
#include
using namespace std;
int main(){
int W, H, i, j, counts = 0;
cin >> W >> H;
if (W % 4 == 0 || H % 4 == 0){
counts = W * H / 2;
}else if(W % 2 == 0 && H % 2 == 0){
counts = (W * H / 4 + 1) * 2;
}
else{
counts = W * H / 2 + 1;
}
cout << counts << endl;
return 0;
}