LCA相关习题：仓鼠找sugar

        首先这是一道LCA。

        题目传送门：https://www.luogu.org/problemnew/show/P3398

        懒人看这边----->题目大意：给你一棵树，每次给出2条路径的起点与中点，问2者有无交叉。

        一开始的方法大伙都可以想到。没错就是暴力。当然不是你想象中的那种超级暴力。这里给出大致思路：

        首先我们找到每对点的LCA，这样便有了2个LCA，之后我们判断这两个LCA谁深度更深，我们这里默认前者深，那么我们接下来只要求出这个LCA与另一对点的LCA，如果这样求出的2个LCA中有一个是之前的LCA那么这两条路径就是相交的。

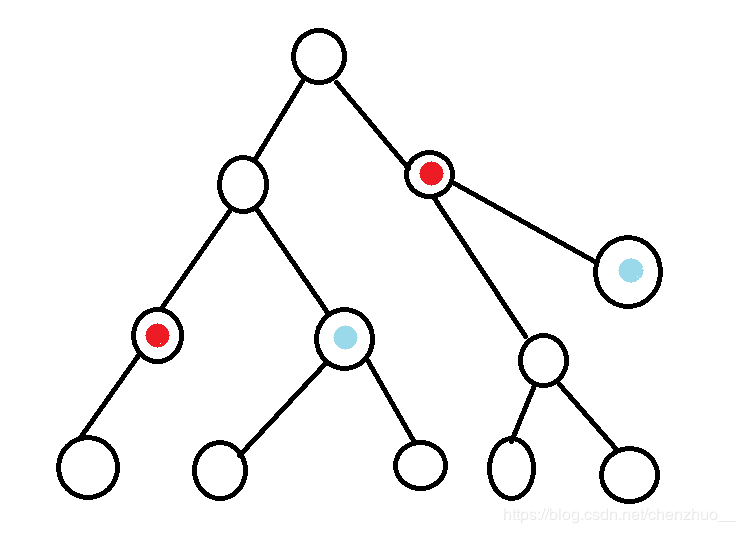
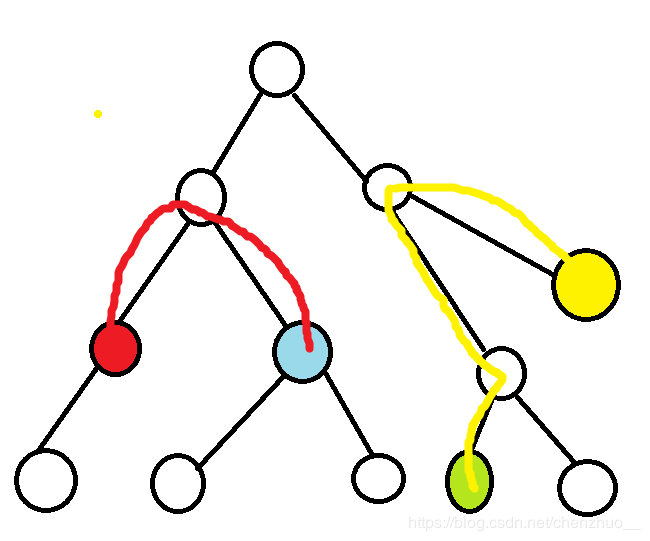
emmmm可能有点……我具体给幅图。不准嫌丑！！！

如图。红色即为一对点，蓝色为另一对点，我接下来把红点的lca求出来。（因为我知道红色的lca深度是最深的（==蓝色））

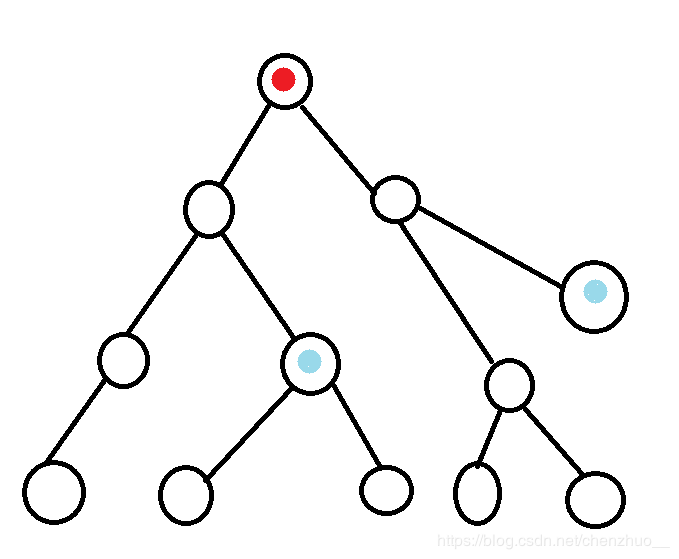
就像这样：

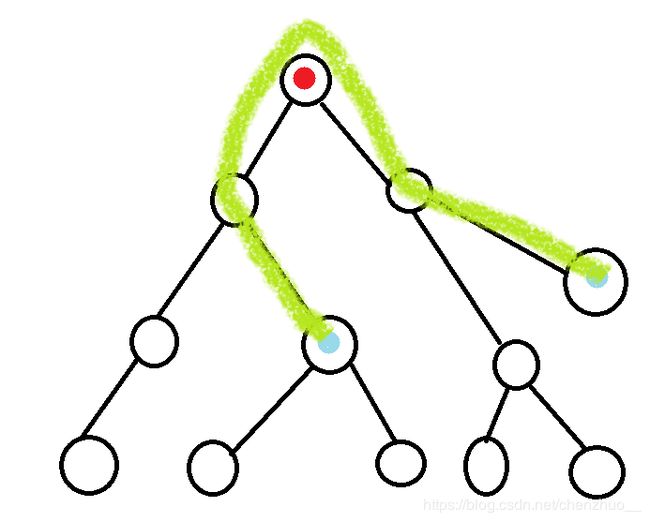
画上蓝色2点之间的路径：

oh♂yes，现在你看出什么端倪了吗？如果说我们以深度较深的lca进行判断，当另外两个点能向上到达这个点的时候，这条路径就一定会碰上lca，因为若要连一条路径必须经过它们的lca，但是这个lca在另一个lca上方，想不经过另一个lca？tan 90°

答案得解！

代码：

#include 
using namespace std;
int n,m,fa[500001][30],head[1050001],tot,deep[1050001],in[1050001],root;
struct node{
    int to,next;
}e[1050001];
inline void add(int x,int y){
    e[++tot].to=y;
    e[tot].next=head[x];
    head[x]=tot;
}
inline void dfs(int x,int father){
    deep[x]=deep[father]+1;
    fa[x][0]=father;
    for(int i=0;++i<=25;)fa[x][i]=fa[fa[x][i-1]][i-1];
    for(int i=head[x];i;i=e[i].next){
        if(e[i].to!=father)dfs(e[i].to,x);
    }
}
inline int lca(int x,int y){
    if(deep[x]=0;)if((1<=0;)
    if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
    return fa[x][0];
}//这里我采用的是倍增 
inline void check(int a,int b,int c,int d){
    int lx=lca(a,b),ly=lca(c,d);
    if(deep[lx]

so？我觉得就一种思路不怎么好。嗯！我得再搞些花头。。。

好！

直截了当，开门见山，方法直接送上！

具体方法：设四个点分别为A,B,C,D,即两条路径为A->B,C->D，那么当且仅当A->B+C->D>=A->C+B->D（此处的->表示从一个点走到另一个点的距离）

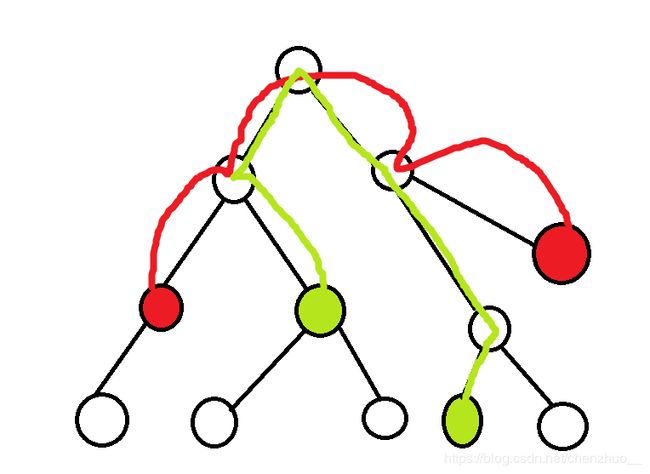
那么为什么是这样呢？其实我一开始也没想到，后面借助哲♂学才有了思路。现在我就再次递上那幅图。。。

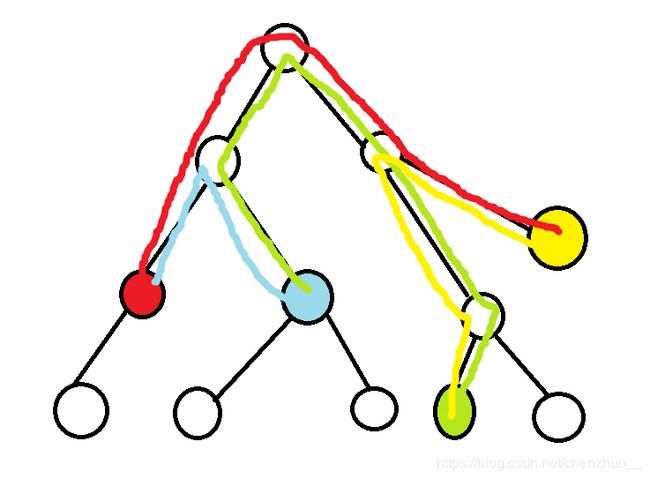
2条路径。

另一种说法的两条路径。（此处黄点即为红点，方便辨认A,B,C,D分别为红，黄，蓝，绿）这里显然1图的路径长度比2图路径长度长。所以2条路径是有相交的。

我现在把2幅图拼在一起你看出什么了吗？（红线和绿线即为一开始的2条路径）

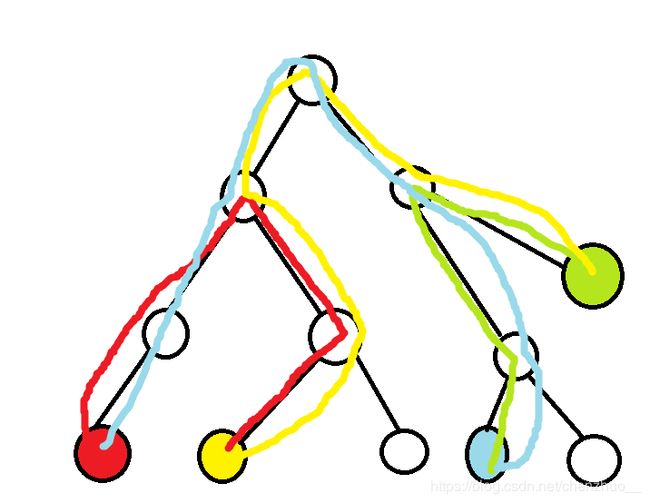
好，现在我再给你一幅图。

现在还是红绿线为原来的路径。请问你又看出什么了？再和上图对比对比？

思考。

先贴代码，后说明原因。

代码：

#include 
using namespace std;
int n,m,fa[500001][30],head[1050001],tot,deep[1050001];
struct node{
	int to,next;
}e[1050001];
inline void add(int x,int y){
	e[++tot].to=y;
	e[tot].next=head[x];
	head[x]=tot;
}
inline void dfs(int x,int father){
	deep[x]=deep[father]+1;
	fa[x][0]=father;
	for(int i=0;++i<=25;)fa[x][i]=fa[fa[x][i-1]][i-1];
	for(int i=head[x];i;i=e[i].next){
		if(e[i].to!=father)dfs(e[i].to,x);
	}
}
inline int lca(int x,int y){
	if(deep[x]=0;)if((1<=0;)
	if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
	return fa[x][0];
}
inline void check(int x1,int x2,int y1,int y2){
	if(deep[x1]+deep[x2]-2*deep[lca(x1,x2)]+deep[y1]+deep[y2]-2*deep[lca(y1,y2)]>=deep[x1]+deep[y1]-2*deep[lca(x1,y1)]+deep[x2]+deep[y2]-2*deep[lca(x2,y2)])printf("Y\n");
	else printf("N\n");
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=0;++i

其实与上面的区别微乎其微，只有check（）内部略有改变。

原因：

当我们一开始从A->B,C->D，走的便是最正常的路，经过了各自的lca，我们通过上面的方法知道了若要2路径相交，则有一个lca必定开了外挂。。。所以呢，当我们改变了走法，变成了A->C,B->D，我们知道A,B的lca是C或D中一个与此的lca，（也可能2个），所以我们改变走法，从A->C，便会减少走向A,B的lca的长度，B->D同理，因此这样的走法总长度就会比一开始的走法短。但是如果一开始2者就没有相交，则我们从A->C不仅会要从A走向A，B的LCA，并且我们还需要从这个LCA走向另一个LCA，再走到C，路途反而增加！B->D同理。并且，我们还可以因此知道具体的相交路径是以较深的两个节点为端点的一条路！

以上。