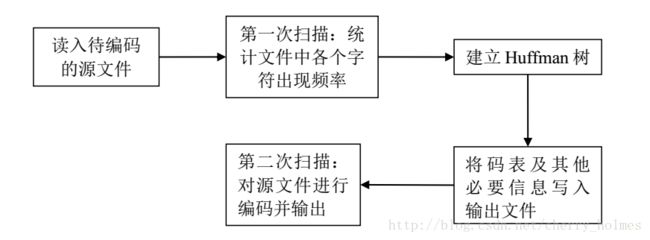
数据压缩原理实验3_Huffman编解码算法实现与压缩效率分析
一、实验原理
1. Huffman编码算法
(1)将文件以ASCII字符流的形式读入,统计每个符号的发生频率;
(2)将所有文件中出现过的字符按照频率从小到大的顺序排列;
(3)每一次选出最小的两个值,作为二叉树的两个叶子节点,将和作为它们的根节点,这两个叶子节点不再参与比较,新的根节点参与比较;
(4)重复3,直到最后得到和为1的根节点;
(5)将形成的二叉树的左节点标0,右节点标1,把从最上面的根节点到最下面的叶子节点途中遇到的0, 1序列串起来,得到了各个字符的编码表示。
2. Huffman编码的数据结构设计
在程序实现中使用一种叫做二叉树的数据结构实现Huffman编码。
(1)哈夫曼节点结构
typedef struct huffman_node_tag //节点数据类型
{
unsigned char isLeaf; //是否为叶节点,1是0否
unsigned long count; //信源文件中出现频数
struct huffman_node_tag *parent; //父节点指针
union
{
struct //如果不是叶节点,那么它为该节点左右子节点的指针
{
struct huffman_node_tag *zero, *one;
};
unsigned char symbol; //如果是叶节点,那么它表示某个信源符号,这里用一个字节的8位二进制数表示
};
} huffman_node;typedef struct huffman_code_tag //码字数据类型
{
unsigned long numbits; //码字的长度(bit)
/* 因为unsign char 类型是以 8 bit 来保存数据,所以码字8个8个一组保存在bits[]中,
例: 码字的第1位存于bits[0]的第1位,
码字的第2位存于bits[0]的第的第2位,
码字的第8位存于bits[0]的第的第8位,
码字的第9位存于bits[1]的第的第1位 */
unsigned char *bits; //指向该码比特串的指针
} huffman_code;该程序包括两个工程,“huff_run”为主工程,其中包括了“huffcode.c”文件
“Huff_code”为库工程,其中包括了“huffman.c”文件
下面按照实验流程来进行分析
3.1 读入待编码的源文件
如下代码属于"huffcode.c"文件
int
main(int argc, char** argv)
{
char memory = 0; //memory为1表示对内存数据进行操作,0表示不操作
char compress = 1; //compress为1表示编码,0表示解码
int opt;
const char *file_in = NULL, *file_out = NULL;
//step1:add by yzhang for huffman statistics
const char *file_out_table = NULL;
//end by yzhang
FILE *in = stdin;
FILE *out = stdout;
//step1:add by yzhang for huffman statistics
FILE * outTable = NULL; //输出的中间数据的表
//end by yzhang
while((opt = getopt(argc, argv, "i:o:cdhvmt:")) != -1) //读取命令行参数的选项
{
switch(opt)
{
case 'i':
file_in = optarg; //i表示输入文件
break;
case 'o':
file_out = optarg; //o表示输出文件
break;
case 'c':
compress = 1; //c表示进行编码
break;
case 'd':
compress = 0; //d表示进行解码
break;
case 'h':
usage(stdout); //h表示输出参数用法说明
return 0;
case 'v':
version(stdout); //v表示输出版本号信息
return 0;
case 'm':
memory = 1; //m表示对内存数据进行操作
break;
// by yzhang for huffman statistics
case 't':
file_out_table = optarg; //t表示输出的中间数据信息
break;
//end by yzhang
default:
usage(stderr);
return 1;
}
}
//如果输入文件给定,那么读取
if(file_in)
{
in = fopen(file_in, "rb");
if(!in)
{
fprintf(stderr,
"Can't open input file '%s': %s\n",
file_in, strerror(errno));
return 1;
}
}
//如果输出文件给定,那么创建
if(file_out)
{
out = fopen(file_out, "wb");
if(!out)
{
fprintf(stderr,
"Can't open output file '%s': %s\n",
file_out, strerror(errno));
return 1;
}
}
//by yzhang for huffman statistics
if(file_out_table)
{
outTable = fopen(file_out_table, "w");
if(!outTable)
{
fprintf(stderr,
"Can't open output file '%s': %s\n",
file_out_table, strerror(errno));
return 1;
}
}
//end by yzhang
if(memory) //对内存数据进行编码或解码操作
{
return compress ?
memory_encode_file(in, out) : memory_decode_file(in, out);
}
//对文件进行编码或解码操作
if(compress) //change by yzhang
huffman_encode_file(in, out,outTable);//step1:changed by yzhang from huffman_encode_file(in, out) to huffman_encode_file(in, out,outTable)
else
huffman_decode_file(in, out);
if(in)
fclose(in);
if(out)
fclose(out);
if(outTable)
fclose(outTable);
return 0;
}3.2 第一次扫描,统计信源字符发生频率
因为是8比特,共256个信源符号,所以创建一个256个元素的指针数组,用以保存256个信源符号的频率。其下标对应相应字符的ASCII码。需要注意的是,源文件中不一定所有的信源符号都会出现,因此数组中存在空元素,而非空元素为待编码文件中实际出现的信源符号。
如下代码属于"huffman.c"文件
#define MAX_SYMBOLS 256
typedef huffman_node* SymbolFrequencies[MAX_SYMBOLS]; //信源符号数组
typedef huffman_code* SymbolEncoder[MAX_SYMBOLS]; //编码后的符号数组/* 第一次扫描,统计信源字符发生频率 */
static unsigned int
get_symbol_frequencies(SymbolFrequencies *pSF, FILE *in)
{
int c;
unsigned int total_count = 0; //将总信源符号数初始化为 0
init_frequencies(pSF); //将所有信源符号地址初始化为NULL(0)
//第一次扫描文件,统计输入文件中每个信源符号的发生频率
while((c = fgetc(in)) != EOF)
{
unsigned char uc = c;
if(!(*pSF)[uc]) // 如果是一个新符号,则产生该字符的一个新叶节点
(*pSF)[uc] = new_leaf_node(uc);
++(*pSF)[uc]->count; //如果已经是叶节点了,则字符发生频数+1
++total_count; //总信源符号数 +1
}
return total_count;
}
对上述代码中的"new_leaf_node"函数进行分析,代码如下:
/*新建一个叶节点,并进行初始化*/
static huffman_node*
new_leaf_node(unsigned char symbol)
{
huffman_node *p = (huffman_node*)malloc(sizeof(huffman_node)); //给该叶节点分配空间
p->isLeaf = 1; //该节点为叶节点
p->symbol = symbol; //该节点存储的信源符号
p->count = 0; //信源符号数为0
p->parent = 0; //该节点的父节点为 NULL
return p;
}
3.3 建立Huffman树并计算符号对应的Huffman码字
(1) 将频率从小到大排序并建立Huffman树
如下代码属于"huffman.c"文件
/* 按频率从小到大顺序排序并建立Huffman树 */
static SymbolEncoder*
calculate_huffman_codes(SymbolFrequencies * pSF)
{
unsigned int i = 0;
unsigned int n = 0;
huffman_node *m1 = NULL, *m2 = NULL;
SymbolEncoder *pSE = NULL;
qsort((*pSF), MAX_SYMBOLS, sizeof((*pSF)[0]), SFComp);
//将信源符号按出现频率大小排序.小概率符号在前,即 pSF数组中下标较小
for(n = 0; n < MAX_SYMBOLS && (*pSF)[n]; ++n) ;//得到文件中所出现的信源符号的种类总数
//因为256种信源符号不一定都会出现
/* 构建霍夫曼树。需要合并n-1次,所以循环n-1次。
该代码基于Ian Witten等人写的第2版 Managing Gigabytes 的第34页中的算法。
注意的事,此实现使用简单计数而不是概率 */
for(i = 0; i < n - 1; ++i)
{
m1 = (*pSF)[0]; //将m1、m2设置为当前频数中最小的两个信源符号
m2 = (*pSF)[1];
//将m1、m2合并为一个新节点加入到数组中
(*pSF)[0] = m1->parent = m2->parent =
new_nonleaf_node(m1->count + m2->count, m1, m2);
(*pSF)[1] = NULL;
//在m1、m2合并后重新排序
qsort((*pSF), n, sizeof((*pSF)[0]), SFComp);
}
//huffman树建好后,从树根开始计算每个符号的码字
pSE = (SymbolEncoder*)malloc(sizeof(SymbolEncoder));
memset(pSE, 0, sizeof(SymbolEncoder));
build_symbol_encoder((*pSF)[0], pSE);
return pSE;
}
对上述代码中的"SFComp"函数进行分析,代码如下:
/* qsort函数使用到的比较函数SFComp,对数组进行从小到大排序 */
static int
SFComp(const void *p1, const void *p2)
{
const huffman_node *hn1 = *(const huffman_node**)p1;
const huffman_node *hn2 = *(const huffman_node**)p2;
//将空节点排序到列表的末尾。
if(hn1 == NULL && hn2 == NULL)
return 0; //如果两个节点都空,返回0,表示相等
if(hn1 == NULL)
return 1; //如果只有第一个节点是空,返回1,表示第二个节点大
if(hn2 == NULL)
return -1; //如果只有第二个节点是空,返回-1,表示第一个节点大
//如果两个节点都不为空,那么进行比较并返回值
if(hn1->count > hn2->count)
return 1;
else if(hn1->count < hn2->count)
return -1;
return 0;
}
对上述代码中的"new_nonleaf_node"函数进行分析,代码如下:
/* 建立内部节点(不是叶节点)*/
static huffman_node*
new_nonleaf_node(unsigned long count, huffman_node *zero, huffman_node *one)
{
huffman_node *p = (huffman_node*)malloc(sizeof(huffman_node)); //分配一个节点的存储空间
p->isLeaf = 0; //说明不是叶节点
p->count = count; //设置符号数
p->zero = zero; //左子节点
p->one = one; //右子节点
p->parent = 0; //无父节点
return p;
}
如下代码属于"huffman.c"文件
static void
build_symbol_encoder(huffman_node *subtree, SymbolEncoder *pSF)
{
if(subtree == NULL) //如果子树为空,则说明编码结束,返回
return;
if(subtree->isLeaf) //如果是是叶节点,则产生码字
(*pSF)[subtree->symbol] = new_code(subtree);//
else //如果不是叶节点,先访问左节点直至到根部后,再访问右节点
{
build_symbol_encoder(subtree->zero, pSF); //通过递归,实现遍历
build_symbol_encoder(subtree->one, pSF);
}
}
/* 从霍夫曼树中的叶子构建一个码字
因为霍夫曼编码是从上往下顺序进行,所以通过从子节点从下往上走到根节点然后反转位来构建huffman代码
*/
static huffman_code*
new_code(const huffman_node* leaf)
{
unsigned long numbits = 0; //码长
unsigned char* bits = NULL; //码字首地址
huffman_code *p;
/* leaf !=0: 当前字符存在,应该编码
leaf->parent !=0: 当前字符的编码仍未完成,即未完成由叶至根的该字符的编码过程
*/
while(leaf && leaf->parent)
{
huffman_node *parent = leaf->parent;
//确定所编bit在当前byte中的位置,因为数组从0-7,刚好用求余来表示
unsigned char cur_bit = (unsigned char)(numbits % 8);
unsigned long cur_byte = numbits / 8; //计算出码字的字节数
/* 如果需要另一个字节去保存码字,则进行再分配 */
if(cur_bit == 0)
{
size_t newSize = cur_byte + 1;
/*realloc 这里很关键,它与malloc不同,
它在保持原有的数据不变的情况下重新分配新的空间,
原有数据存在新空间中的前面部分(这里空间的地址可能有变化)*/
bits = (char*)realloc(bits, newSize);
bits[newSize - 1] = 0; //初始化新分配的8bit(1字节)为0
}
if(leaf == parent->one) //判断是否为右子节点,Huffman树左0右1
bits[cur_byte] |= 1 << cur_bit; //若是,则左移1至当前byte的当前位
++numbits; //码长加1
leaf = parent; //将下一个节点挪至父节点处
}
/* 因为编码是从根到叶 即将树从上往下,所以需要码字逆序*/
if(bits)
reverse_bits(bits, numbits);
p = (huffman_code*)malloc(sizeof(huffman_code));
p->numbits = numbits;
p->bits = bits; //整数个字节。与numbits配合才可得到真正码字
return p;
}
/* 码字逆序 */
static void
reverse_bits(unsigned char* bits, unsigned long numbits)
{
unsigned long numbytes = numbytes_from_numbits(numbits); //存储码字需要的字节数
unsigned char *tmp =
(unsigned char*)alloca(numbytes); //alloca 适用于堆栈上的空间,可自动释放
unsigned long curbit;
long curbyte = 0;
memset(tmp, 0, numbytes);
for(curbit = 0; curbit < numbits; ++curbit)
{
unsigned int bitpos = curbit % 8; //判断当前位在字节中的位数
if(curbit > 0 && curbit % 8 == 0)
++curbyte; //当bit数超出8 那么字节数加1
//从后往前取码字中的每一位,再移位到所在字节的正确位置
tmp[curbyte] |= (get_bit(bits, numbits - curbit - 1) << bitpos);
}
memcpy(bits, tmp, numbytes);
}
/* 化bit为byte处理 */
static unsigned long
numbytes_from_numbits(unsigned long numbits)
{
return numbits / 8 + (numbits % 8 ? 1 : 0); //确定字节数,利用取整+是否有余数来确定(8位一字节)
}
/* get_bit返回位数返回值的第 i/8 个字节的第 i%8 位。*/
static unsigned char
get_bit(unsigned char* bits, unsigned long i)
{
return (bits[i / 8] >> i % 8) & 1;
}
3.4 将Huffman码表写入文件
如下代码属于"huffman.c"文件
/*
编写huffman代码表。 格式为:
4字节,以网络字节顺序排列。
4字节编码的字节数
(如果对数据解码,应该得到这个字节数)
code1
...
codeN,其中N是在文件开始时读取的计数。
每个 odei 具有以下格式:
1字节符号,1字节位长度。
每个条目都有numbytes_from_numbits个字节。
如果码字中的位数不是8的倍数,则每个码字的最后一个字节可能有额外的位。
*/
/* 将码表输出到输出文件 */
static int
write_code_table(FILE* out, SymbolEncoder *se, unsigned int symbol_count)
{
unsigned long i, count = 0;
for(i = 0; i < MAX_SYMBOLS; ++i) /// 确定文件中码字的实际种类,并保存在se中
{
if((*se)[i])
++count;
}
/* 把字节种类数和字节总数以网络传输中的顺序写入文件中 */
i = htonl(count);
//在网络传输中,采用big-endian序,对于0x0A0B0C0D ,传输顺序就是0A 0B 0C 0D ,
//因此big-endian作为network byte order,little-endian作为host byte order。
//little-endian的优势在于unsigned char/short/int/long类型转换时,存储位置无需改变
if(fwrite(&i, sizeof(i), 1, out) != 1)
return 1;
symbol_count = htonl(symbol_count); // 写入要被编码的字节种类的个数
if(fwrite(&symbol_count, sizeof(symbol_count), 1, out) != 1)
return 1;
// 写入码表中
for(i = 0; i < MAX_SYMBOLS; ++i)
{
huffman_code *p = (*se)[i];
if(p)
{
unsigned int numbytes; //字节数
fputc((unsigned char)i, out); //写入字节符号
fputc(p->numbits, out); //写入码长
numbytes = numbytes_from_numbits(p->numbits); //写入码字
if(fwrite(p->bits, 1, numbytes, out) != numbytes)
return 1;
}
}
return 0;
}
3.5 第二次扫描,对文件查表进行Huffman编码,并输出
如下代码属于"huffman.c"文件
static int
do_file_encode(FILE* in, FILE* out, SymbolEncoder *se)
{
unsigned char curbyte = 0;
unsigned char curbit = 0;
int c;
while((c = fgetc(in)) != EOF) //对文件进行遍历
{
unsigned char uc = (unsigned char)c;
huffman_code *code = (*se)[uc]; //进行查表
unsigned long i;
for(i = 0; i < code->numbits; ++i) //将码字写入文件
{
curbyte |= get_bit(code->bits, i) << curbit;//把当前比特位加到编码字节的相应位置
//如果该字节被填满,则写入该字节并重新设置curbit和curbyte。
if(++curbit == 8)
{
fputc(curbyte, out);
curbyte = 0;
curbit = 0;
}
}
}
//如果有数据未输出,则表示最后一个编码字符未落在字节边界上,然后输出。
if(curbit > 0)
fputc(curbyte, out);
return 0;
}
下图为输出的huffman编码文件的存储示意图:

4. Huffman解码

4.1 读取码表并重建据此Huffman树
如下代码属于"huffman.c"文件
static huffman_node*
read_code_table(FILE* in, unsigned int *pDataBytes)
{
huffman_node *root = new_nonleaf_node(0, NULL, NULL);
unsigned int count;
if(fread(&count, sizeof(count), 1, in) != 1)// 读取码表中的符号数
{
free_huffman_tree(root);
return NULL;
}
count = ntohl(count);
//读取此编码表示的数据字节数
if(fread(pDataBytes, sizeof(*pDataBytes), 1, in) != 1)
{
free_huffman_tree(root);
return NULL;
}
*pDataBytes = ntohl(*pDataBytes);
while(count-- > 0) //读取码表,由符号、码长、码字三部分组成
{
int c;
unsigned int curbit;
unsigned char symbol; //符号
unsigned char numbits; //码长
unsigned char numbytes; //字节数
unsigned char *bytes;
huffman_node *p = root;
if((c = fgetc(in)) == EOF) //一个字节一个字节的读入
{
free_huffman_tree(root);
return NULL;
}
symbol = (unsigned char)c;
if((c = fgetc(in)) == EOF)
{
free_huffman_tree(root);
return NULL;
}
numbits = (unsigned char)c;
numbytes = (unsigned char)numbytes_from_numbits(numbits); //计算保存一个码长所需要的字节数
bytes = (unsigned char*)malloc(numbytes); // 为读取码字分配相应的空间
if(fread(bytes, 1, numbytes, in) != numbytes) // 读取码字
{
free(bytes);
free_huffman_tree(root);
return NULL;
}
//根据码表,进行huffman树的重建,由根节点至叶节点
for(curbit = 0; curbit < numbits; ++curbit)
{
if(get_bit(bytes, curbit)) // 判断当前读取位是否为’1’
{ //若当前读取位为'1'
if(p->one == NULL) //建立右子节点
{
//判断是否是当前码字的最后一位,若是,新建叶结点;若不是,则新建非叶结点。
p->one = curbit == (unsigned char)(numbits - 1)
? new_leaf_node(symbol)
: new_nonleaf_node(0, NULL, NULL);
p->one->parent = p; //设置右子节点的父节点
}
p = p->one;
}
else //若当前读取位为'0'
{
if(p->zero == NULL) //建立左子节点
{
p->zero = curbit == (unsigned char)(numbits - 1)
? new_leaf_node(symbol)
: new_nonleaf_node(0, NULL, NULL);
p->zero->parent = p;
}
p = p->zero;
}
}
free(bytes);
}
return root; // 返回Huffman树的根结点,才可以进行之后的遍历
}
4.2 读取Huffman码字,并根据huffman树进行解码输出
如下代码属于"huffman.c"文件
int
huffman_decode_file(FILE *in, FILE *out)
{
huffman_node *root, *p;
int c;
unsigned int data_count;
root = read_code_table(in, &data_count); //读取码表
if(!root)
return 1; // Huffman树建立失败
// 文件解码
p = root;
// data_count >0 :逻辑上仍有数据;(c = fgetc(in)) != EOF):文件中仍有数据
while(data_count > 0 && (c = fgetc(in)) != EOF)
{
unsigned char byte = (unsigned char)c; //一个字节的码字
unsigned char mask = 1; // mask用于逐位读出码字
while(data_count > 0 && mask)
{
//走huffman树,若当前字节为0,就走左子树,否则走右子树
p = byte & mask ? p->one : p->zero;
mask <<= 1; //mask每个循环进行左移
if(p->isLeaf) //走到叶结点,标明解码完毕
{
fputc(p->symbol, out); //输出叶节点中存储的符号
p = root; //转向根节点,进行下一个码字的解码
--data_count; //将没解码的码字数-1
}
}
}
free_huffman_tree(root); // 所有码字均已解码输出,文件解码完毕
return 0;
}
二、实验结果
选择十种不同格式类型的文件,使用Huffman编码器进行压缩得到输出的压缩比特流文件,并对各种不同格式的文件进行压缩效率的分析
分析结果如下:
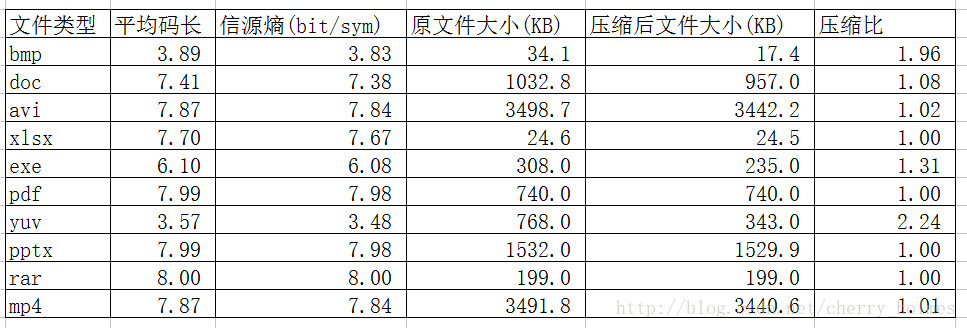
1. 表格形式表示的实验结果
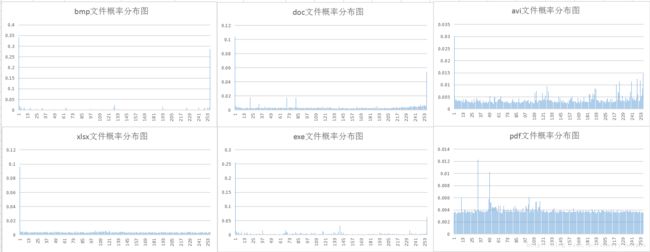
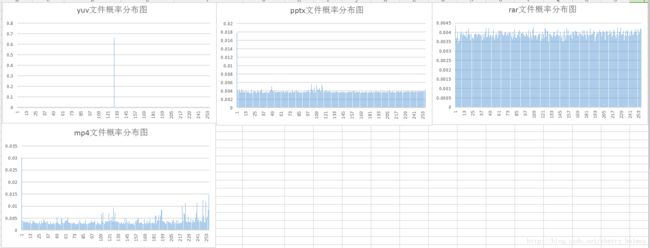
2. 各样本文件的概率分布图
3. 实验结果的分析
可以从表格和概率分布图看出,huffman编码的平均码长小于且很接近信源熵,信源熵一定小于8bit/sym
当文件分布概率越不均匀,编码效率越高(如yuv文件);当文件分布概率比较均匀时,压缩效果并不理想