机器学习 -- 模型集成与调优

一、数据集介绍

1. 样本介绍

本数据集为患者乳腺癌患病检测样本，共有569个，它的前两列为唯一的ID号和诊断结果（M= malignant，B=benign），它的3-> 32列为实数值特征。

2. 读入数据，查看样本

import pandas as pd
df=pd.read_csv('http://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/wdbc.data', header=None) # 读取数据集
df.head()

二、使用Piprline简化数据预处理过程

1. Pipeline介绍

在训练机器学习算法的过程中，我们用到了不同的数据预处理技术，比如：标准化，PCA等。在scikit-learn 中我们可以使用pipeline这个非常方便的类帮我们简化这些过程，这个类可以帮我们用任意次的转换步骤来拟合模型并预测新的数据。

2. 拆分训练集&测试集，并将类别变量转化为0-1标签

from sklearn.preprocessing import LabelEncoder
X = df.loc[:, 2:].values #抽取训练集特征
y = df.loc[:, 1].values #抽取训练集标签
le = LabelEncoder()
y=le.fit_transform(y)  # 把字符串标签转换为整数，恶性-1，良性-0

from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=1)   # 拆分成训练集(80%)和测试集(20%)

3.数据集预处理—- 标准化及降维处理

# 用标准化和PCA（30维--》 2维）对数据进行预处理，用Piprline类把这些过程链接在一起
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline

# 用StandardScaler和PCA作为转换器，LogisticRegression作为评估器
estimators=[('scl',StandardScaler()),('pca',PCA(n_components=2)),('clf',LogisticRegression(random_state=1))]
# Pipeline类接收一个包含元组的列表作为参数，每个元组的第一个值为任意的字符串标识符，
# 比如：我们可以通过pipe_lr.named_steps['pca']
# 来访问PCA组件;第二个值为scikit-learn的转换器或评估器
pipe_lr = Pipeline(estimators)
pipe_lr.fit(X_train, y_train)
print(pipe_lr.score(X_test,y_test))  
# 0.947368421053   

4.Pipeline 处理流程可概括如下图所示

三、 用k-fold交叉验证评估模型性能

在上面的例子中，我们只是将数据集分成了训练集和测试集，然而在实际的机器学习应用中，我们会选择最优的模型和最优的学习参数来提高我们算法对未见到数据预测的性能。然而，如果在模型选择或调节参数时，选择相同的测试集，这样很有可能模型只适用于当前的测试集，对其他数据集适应性不好，易出现过拟合现象。

因此，更好的解决办法是我们将数据集分成三部分：训练集，交叉验证集，测试集。构建机器学习系统的步骤为：

1）选择模型和参数，用训练集去拟合
2）把拟合后的模型和参数应用到交叉验证集来评估其性能
3）不断地重复1，2两个过程，直到挑选出满意的模型和参数
4）用测试集去评估步骤3中选出的模型，看它在未见过的数据上的性能

1.holdout交叉验证

将训练集拆分成训练集和交叉验证集

2.k-fold交叉验证

将训练集拆分成k份，k-1份做训练，1份用作测试，然后把k份中的每份都用来测试，剩下的用作训练，因此会得到k个模型和性能的评估，最后求出性能的平均值

上图中我们把训练集分成10份，在10次迭代中，9分被用作训练集，1次被用作测试，最后求出平均性能。
注意：
在每次迭代中，我们并没有重新划分训练集，我们只是最初分成10份，接着在每次迭代中，用这10份中的每一份做测试剩下的9份用作训练。

scikit-learn中，对k-fold交叉验证做了小小的改进，即每份的训练中都有相同的类别比例。代码如下：

scores = []
kfold = StratifiedKFold(y=y_train, n_folds=10, random_state=1) #n_folds参数设置为10份
for train_index, test_index in kfold:
    pipe_lr.fit(X_train[train_index],y_train[train_index])
    score = pipe_lr.score(X_train[test_index],y_train[test_index])
    scores.append(score)
    print('类别分布: %s, 准确度: %.3f' % (np.bincount(y_train[train_index]),score))    
np.mean(scores) #求出评估的平均值

通过scikit-learn pipeline方法自动实现上述步骤：

#下面的n_jobs参数可以指定我们机器上的多个CPU来评估我们每份不同的训练集，这是一个非常有用的参数。
from sklearn.cross_validation import cross_val_score
scores = cross_val_score(estimator=pipe_lr, X=X_train, y=y_train, cv=10, n_jobs=1)
print(scores)

四、 学习曲线和验证曲线

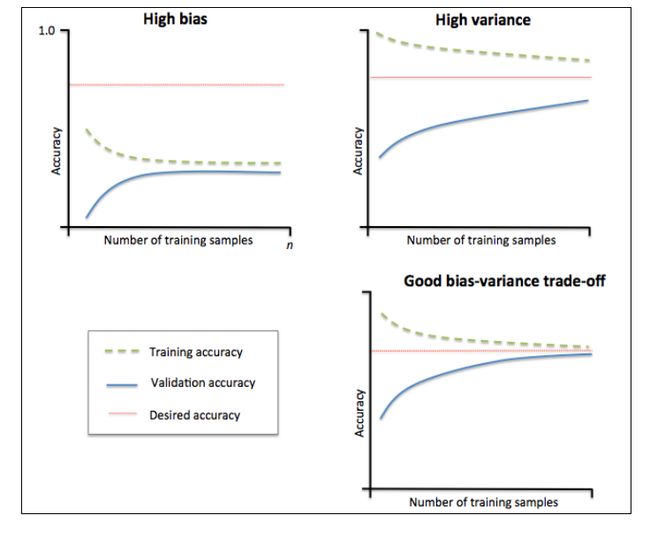
通过绘制模型训练和验证准确性关于训练集大小的函数，我们能很容易地诊断出模型是高方差还是高偏差。

1.学习曲线

1）左上角图
高偏差，代表这个模型的训练准确性和交叉验证准确性都很低，表明模型欠拟合。
解决高偏差（欠拟合）问题： 通常增加模型的参数，比如构造更多的样本特则会那个或减小正则化的程度
2）右上角图
高方差，该模型在训练集准确性和交叉验证集准确性之间有很大的缺口，这表明模型很好地拟合了数据集，但对未见过的数据效果很差。说明模型存在过拟合问题。
解决高方差（过拟合）问题：收集更多的数据或者降低模型的复杂度

2. 绘制学习曲线

#绘制学习曲线
from sklearn.learning_curve import learning_curve
import matplotlib.pyplot as plt
pipe_lr = Pipeline([('scl',StandardScaler()),('clf',LogisticRegression(penalty='l2',random_state = 0))])
train_sizes, train_scores, test_scores = learning_curve(estimator=pipe_lr, X=X_train, y=y_train)
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores,axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)
plt.plot(train_sizes, train_mean, color='blue',marker='o',markersize=5, label='training accuracy')
plt.fill_between(train_sizes, train_mean + train_std,train_mean - train_std, alpha=0.15, color='blue' )
plt.plot(train_sizes, test_mean, color='green', linestyle='--',marker='s',markersize=5, label='validation accuracy')
plt.fill_between(train_sizes, test_mean + test_std, test_mean - test_std, alpha=0.15, color='green')
plt.grid()
plt.xlabel('Number of training samples')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.ylim([0.8, 1.0])
plt.show()

从上面的图形中我们可以看出，模型在交叉训练集上表现地很好，但是有点过拟合，因为在两个曲线之间有一点明显的间隔

3. 验证曲线

学习曲线是训练集数量与准确性之间的函数，而验证曲线是不同的模型参数与准确性之间的函数。具体代码如下：

#绘制验证曲线
from sklearn.learning_curve import validation_curve

param_range = [0.001, 0.01, 0.1, 1.0, 10.0, 100.0]
train_scores, test_scores = validation_curve(estimator=pipe_lr, X=X_train, y=y_train, param_name='clf__C', param_range=param_range, cv=10)

train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)

plt.plot(param_range, train_mean, color='blue', marker='o', markersize=5, label='training accuracy')
plt.fill_between(param_range, train_mean + train_std, train_mean - train_std, alpha=0.15, color='blue')
plt.plot(param_range, test_mean, color='green', linestyle='--', marker='s', markersize=5, label='validation accuracy')
plt.fill_between(param_range, test_mean + test_std, test_mean - test_std, alpha=0.15, color='green')

plt.grid()
plt.xscale('log')
plt.legend(loc='lower right')
plt.xlabel('Parameter C')
plt.ylabel('Accuracy')
plt.ylim([0.8, 1.0])
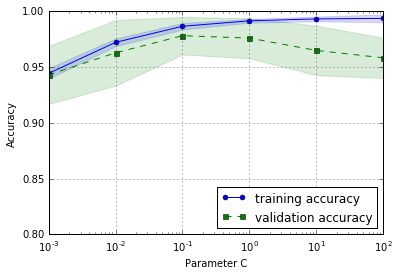
plt.show()

从上图中可以看出，随着参数C的增大，模型有点过拟合数据，因为C越大，就意味着正则化的强度越小。然而对于小的参数C来说，正则化的强度很大，模型有点欠拟合。从图形中反馈得知，C在0.1左右是最好的

五、 通过网格搜索（grid search）微调机器学习模型

在机器学习应用中，有两种类型的参数：

• 一个是从训练集中学得的参数，里例如逻辑回归的权重；
• 另一个是为了使学习算法达到最优化可调节的参数，例如逻辑回归中的正则化参数或决策树中的深度参数，这种可调节的参数称为超参数（hyperparameters）

上面的例子中，我们使用验证曲线调节超参数中的一个参数来优化模型，接下来我们通过网格搜索超参数优化工具来找到超参数的最优组合从而进一步改善模型的性能

网格搜索思路： 列举出所有想要的参数，然后琼剧出所有参数组合，最后得出一个使模型最好的参数组合。

下面来调节SVM分类器的C， kernel，gamma参数，
代码如下：

# grid search 模型调优
from sklearn.grid_search import GridSearchCV
from sklearn.svm import SVC

pipe_svc = Pipeline([('scl', StandardScaler()), ('clf', SVC(random_state=1))])
param_range = [0.0001, 0.001, 0.01, 0.1, 1.0, 10.0, 100.0, 1000.0]
param_grid = [{'clf__C': param_range, 'clf__kernel': ['linear']}, {'clf__C': param_range, 'clf__gamma': param_range, 'clf__kernel': ['rbf']}]

gs = GridSearchCV(estimator=pipe_svc, param_grid=param_grid, scoring='accuracy', cv=10, n_jobs=-1)
gs = gs.fit(X_train, y_train)
print(gs.best_score_)
# 0.978021978022
print(gs.best_params_)
# {'clf__C': 0.1, 'clf__kernel': 'linear'}
clf= gs.best_estimator_
clf.fit(X_train,y_train)
print('Test accuracy: %.3f' % clf.score(X_test,y_test))
#Test accuracy: 0.965

六、 性能指标值precision，recall 和 F1-score

1. 度量模型的性能指标不仅仅是它的准确性，还有precision （PRE），recall （REC）和 F1-score。

PRE = (TP + TN)/(TP + FP + FN + TN)
REC = TP/（TP + FN）

实际中将两者组合，形成 F1-score
F1=2* PRE * REC/（PRE + REC）

2.scikit-learn 中实现混淆矩阵

# scikit-learn 计算混淆矩阵
from sklearn.metrics import confusion_matrix
pipe_svc.fit(X_train,y_train)
y_pred = pipe_svc.predict(X_test)
confmat = confusion_matrix(y_true=y_test, y_pred=y_pred)
print(confmat)
# [[71  1]
# [ 2 40]]

3.matplotlib的matshow绘制混淆矩阵

fig,ax= plt.subplots()
ax.matshow(confmat, cmap=plt.cm.Blues, alpha=0.3)
for i in range(confmat.shape[0]):
    for j in range(confmat.shape[1]):
        ax.text(x=j, y=i, s=confmat[i,j],va='center', ha='center')

plt.xlabel('predicted label')
plt.ylabel('true label')
plt.show() 

4.scikit-learn 计算不同的误差评价标准

#计算不同的误差评价标准。
from sklearn.metrics import precision_score, recall_score,f1_score
precision_score(y_true=y_test,y_pred=y_pred)
# 0.97560975609756095
recall_score(y_true=y_test,y_pred=y_pred)
# 0.95238095238095233
f1_score(y_true=y_test,y_pred=y_pred)
# 0.96385542168674698

七、 ROC曲线

1.ROC曲线介绍

ROC是一种选择分类模型的工具
ROC曲线横坐标： TPR = TP/（FN+ TP） — 真正类率
纵坐标： FPR = FP/（TN + FP） — 负正类率
在ROC曲线中，左下角是将所有样例判为反例的情况，而右上角的点是将所有样例判为正例的情况。

2.Python绘制ROC曲线

from sklearn.metrics import roc_curve, auc
from scipy import interp

X_train2 = X_train[:, [4,14]]
cv = StratifiedKFold(y_train, n_folds=3, random_state=1)
fig = plt.figure()

mean_tpr=0.0
mean_fpr=np.linspace(0,1,100)
all_tpr = []

# plot 每个fold的ROC曲线，这里fold的数量为3,被StratifiedKFold指定
for i, (train,test) in enumerate(cv):
    #返回预测的每个类别（这里为0或1）的概率
    probas = pipe_lr.fit(X_train2[train],y_train[train]).predict_proba(X_train2[test])
    fpr,tpr,thresholds = roc_curve(y_train[test],probas[:,1],pos_label=1)
    mean_tpr += interp(mean_fpr, fpr,tpr)
    mean_tpr[0]=0.0
    roc_auc=auc(fpr,tpr)
    plt.plot(fpr,tpr,linewidth=1,label='ROC fold %d (area = %0.2f)' % (i+1, roc_auc))

# plot random guessing line
plt.plot([0,1],[0,1],linestyle='--',color=(0.6,0.6,0.6),label='random guessing')
mean_tpr /= len(cv)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
plt.plot(mean_fpr, mean_tpr, 'k--', label='mean ROC (area = %0.2f)' % mean_auc, lw=2)

# plot perfect performance line
plt.plot([0, 0, 1], [0, 1, 1], lw=2, linestyle=':', color='black', label='perfect performance')

# 设置x,y坐标范围
plt.xlim([-0.05,1.05])
plt.ylim([-0.05,1.05])
plt.xlabel('false positive rate')
plt.ylabel('true positive rate')
plt.title('Receiver Operator Charateristic')
plt.legend(loc='lower right')
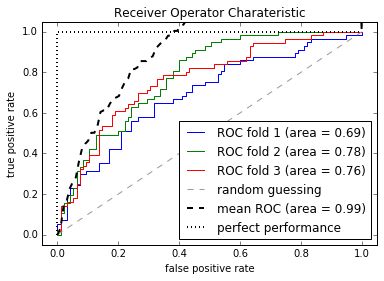
plt.show()

3.AUC —ROC曲线下面的面积，衡量模型的性能

本文参考自：http://blog.csdn.net/xlinsist/article/details/51344449