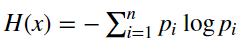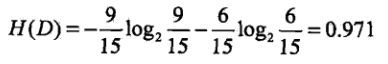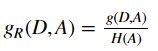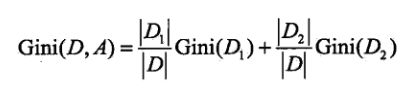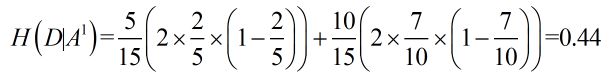《统计学习方法》—— 5.决策树(Python实现)
本文主要是在阅读过程中对本书的一些概念摘录,包括一些个人的理解,主要是思想理解不涉及到复杂的公式推导。若有不准确的地方,欢迎留言指正交流
本文完整代码见 github : https://github.com/anlongstory/awsome-ML-DL-leaning/lihang-reading_notes (欢迎 Star )
5.决策树
决策树(decision tree)是一种基本的分类与回归方法,本文主要讨论分类的决策树。
通常决策树包含:特征选择,决策树生成,决策树的修剪。
特征选择
这里主要是通过递归来选择最优的特征,这里首先要了解 熵,经验熵,经验条件熵,信息增益 的概念及相关关系。
熵 H(X):表示随机变量不确定性的变量,不确定性越大,熵越大。
设 X 是有限个的离散随机变量,X的熵定义为:
其中 pi 为 Xi 的概率分布。 这里信息熵对数以 2 为底或以 e 为底,熵的单位分别为比特(bit) 或 纳特(nat)。
条件熵 H(Y|X): 表示已知随机变量 X 的条件下随机变量 Y 的不确定性。
定义为 X 给定条件下 Y 的条件概率分布的熵对 X 的数学期望:
其中 pi 为 Xi 的概率分布。
当熵与条件熵中的概率由数据估计(尤其是极大似然估计)得到时,对应的熵和条件熵就是经验熵(empirical entropy) 和经验条件熵(empirical conditional emtropy)。
相关代码:(详见info_gain.py)
# 经验熵
def entropy(datasets):
data_length = len(datasets)
label_count = {}
for i in range(data_length):
label = datasets[i][-1]
if label not in label_count:
label_count[label] = 0
label_count[label]+=1
ent = -sum([( p/data_length) * log(p/data_length,2)
for p in label_count.values()])
return ent
# 经验条件熵
def condition_entropy(datasets,axis = 0):
data_length = len(datasets)
feature_sets = {}
for i in range(data_length):
feature = datasets[i][axis]
if feature not in feature_sets:
feature_sets[feature] = []
feature_sets[feature].append(datasets[i])
condi_ent = sum([ (len(p) / data_length)*entropy(p)
for p in feature_sets.values()])
return condi_ent
信息增益: 经验熵与条件经验熵之差
代码:
# 信息增益
def info_gain(ent,condi_entropy):
return ent - condi_entropy
训特征 A 在训练集 D 上的信息增益定义式为:
例5.1
这里将上述表格的信息进行一个归纳总结,总共有 4 个特征,然后每个特征对应最后的类别为 是/否 :
| 特征 | 分布 |
|---|---|
| A1 年龄 | { 5青年 : [2是 3否] } { 5中年 : [ 3是 2否 ] } { 5老年 : [ 4是 1否 ] } |
| A2 工作 | { 10没有工作 : [ 4是 6否 ] } { 5有工作 : [ 5是 ] } |
| A3 有房子 | {9没有房子 : [ 3是 6否 ] } { 6有房子 : [ 6是 ] } |
| A4 信贷 | { 6好 : [4是 2否] } { 5一般 : [ 1是 4否 ] } { 4非常好 : [ 4是 ] } |
| 类别 D | 9 是 6 否 |
以其中一个归纳举例,{ 5青年 : [2是 3否] } 表示 A1年龄 这个特征中 有 5 个是青年,5个青年中有 2 个批准申请贷款,3个不批准申请贷款,依次类推。
根据上面的定义式:
经验熵 H(D):
因为其中 类别 D 有 9 个是批准,6个不批准。
条件经验熵 H(D|A1):
最后求得H(D|A1) = 0.888 。
这里得 D1,D2,D3,分别对应 青年,中年,老年,括号里的概率分别对应青年,中年,老年中的 是 和 否 的个数。
依次类推可以计算得到 H(D|A2), H(D|A3), H(D|A4)。
信息增益g(D,A1):
根据定义式可得:
g(D,A1) = H(D) - H(D|A1) = 0.971 - 0.888 = 0.083
同理可得:
g(D,A2) = H(D) - H(D|A2)= 0.971 - 0.647 = 0.324
g(D,A3) = H(D) - H(D|A3)= 0.971 - 0.551 = 0.420
g(D,A4) = H(D) - H(D|A4)= 0.971 - 0.608 = 0.363
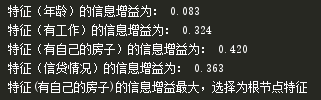
代码运行结果:
这里新增一个概念 信息增益比:
信息增益比: 信息增益与经验熵之比
特征 A 对训练集 D 的信息增益为 g(D|A),经验熵为 H(D):
决策树的生成
主要介绍两种算法,
- ID3 算法 (见 DecisionTree.py)
ID3 算法:在各个节点上应用 信息增益 准则来选择特征,递归地构建决策树。
而 ID3 算法只有树的生成,所以产生的树容易过拟合。因此 C4.5 可以看作是对 ID3 算法的改进。
- C4.5 算法
C4.5 算法: 在各个节点上应用信息增益比 来选择特征,递归地构建决策树,并进行了剪枝。
决策树剪枝
主要是在决策树学习的损失函数中加入了 叶节点个数 的因素。 将 |T|*α 作为惩罚项,自下而上递归地将叶节点回缩以后再计算损失函数的值,如果损失函数的值有减小,就删除当前节点,其中 α 为系数,|T| 为当前决策树 T 的叶节点个数,这里 α 越大,模型(树)越简单,α 越小,模型(树)越复杂。
决策树生成只考虑通过提高信息增益(或信息增益比)对训练集进行拟合,剪枝也是在损失函数中加入了模型复杂度(叶节点的个数)的因素。所以生成时学习的是局部的模型,剪枝学习的是整体的模型。
CART 算法
CART (classification and regression tree,分类与回归树)模型是在给定输入随机变量 X 下输出随机变量 Y 的条件概率分布的学习方法。
分成两步构成:
- 决策树生成:对回归树用 平方误差 最小化准则,对分类树用 基尼指数 最小化准则,进行特征选择生成决策树。
- 决策树剪枝: 首先从生成算法生成的树的底端不断剪枝,直到根节点,形成一个子树序列,然后通过交叉验证法在独立的验证数据集上进行测试,从中选择最优子树。
决策树生成
这里主要介绍分类树的生成,及基尼指数。
基尼指数:分类问题中,假设有 K 类,样本点属于第 k 类的概率为 pk ,则概率分布的基尼指数定义为:
对于二分类问题,第一类的概率为 p,则概率分布的基尼指数为:
如果样本集合 D 根绝特征 A 是否取某一个可能值 a 被分割成 D1,和D2 两部分,则在特征 A 的条件下,集合 D 的基尼指数定义为:
以上述例5.1为例,年龄特征 A1 :青年,中年,老年 会分别划分为:
Gini(D,A1 = 1) 对应 D1 = 青年,D2 = 中年,老年
Gini(D,A1 = 2) 对应 D1 = 中年,D2 = 青年,老年
Gini(D,A1 = 3) 对应 D1 = 老年,D2 = 青年,中年
依次类推。 |Di| 指对应类别的样本总数,|D| 表示集合总样本数。
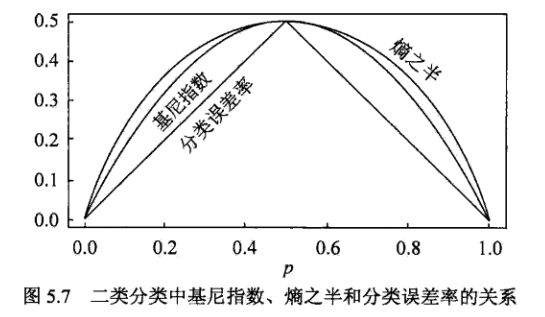
基尼指数 Gini(D) 表示集合 D 的不确定性,Gini(D,A) 表示经 A=a 分割后集合 D 的不确定性。基尼指数值越大,样本集合的不确定性就越大,与熵相似。
基尼指数的作用
基尼指数主要是用来选择 最优特征 和 最优切分点 的。
仍然以例5.1为例,对特征 A1,A2,A3,A4,分别求对应的:
Gini(D,A1)
Gini(D,A1 = 1) = 0.44
Gini(D,A1 = 2) = 0.48
Gini(D,A1 = 3) = 0.44Gini(D,A2)
Gini(D,A2 = 1) = 0.32Gini(D,A3)
Gini(D,A3 = 1) = 0.27 # 所有基尼指数中的最小值Gini(D,A4)
Gini(D,A4 = 1) = 0.36
Gini(D,A4 = 2) = 0.47
Gini(D,A4 = 3) = 0.32
由上面可以看到,Gini(D,A3 = 1)=0.27 最小,所以选择特征 A3 为最优特征,A3 = 1 为最优分割点。 对另一个节点 A1,A2,A4,继续使用这个方法计算最优特征及最优切分点,依次类推,构建决策树。
相关阅读:
《统计学习方法》—— 1. 统计学习方法概论(Python实现)
《统计学习方法》—— 2. 感知器(Python实现)
《统计学习方法》—— 3. K近邻法(Python实现)
《统计学习方法》—— 4. 朴素贝叶斯(Python实现)
《统计学习方法》—— 6. 逻辑斯特回归与最大熵模型(Python实现)
《统计学习方法》—— 7. 支持向量机(Python实现)
《统计学习方法》—— 8. 提升方法 (Python实现)
《统计学习方法》—— 9. EM 算法(Python实现)
《统计学习方法》——10. 隐马尔可夫模型(Python实现)
《统计学习方法》—— 11. 条件随机场