机器学习: 决策数与随机森林
文章目录
- Github
- 数学基础
- 概率公式
- 先验概率与后验概率
- 信息熵
- 互信息
- 条件熵
- 决策树
- 信息增益
- 信息增益率
- 基尼系数
- 决策树生成
- 决策树剪枝
- Bagging 与 随机森林
- Bagging
- 随机森林
Github
系列文章 pdf 版本已经上传至: https://github.com/anlongstory/awsome-ML-DL-leaning/tree/master/xiaoxiang-notes
欢迎 Star 和下载
数学基础
概率公式
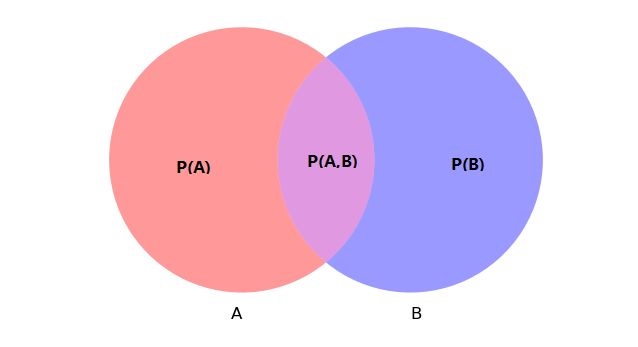
这里用 Venn 图来表示事件A 与事件 B 的关系, P ( A ) P(A) P(A) 与 P ( B ) P(B) P(B) 分别表示它们各自发生的概率,其中它们的交叠区域用 P ( A , B ) P(A,B) P(A,B) 表示 A 和 B 共同发生的概率。 基于上面的表示,可以给出条件概率的公式:
P ( A ∣ B ) = P ( A , B ) P ( B ) P(A|B)= \frac{P(A,B)}{P(B)} P(A∣B)=P(B)P(A,B)
条件概率公式(1)表示,在事件 B 发生的条件下,事件 A 发生的概率,结合上面的 Venn 图不难理解这个公式,将(1)转换一下并推广,可以得到全概率公式,事件组{ B i B_i Bi} 是样本空间的一个划分:
P ( A ) = ∑ i = 1 n P ( B i ) P ( A ∣ B i ) P(A)= \sum_{i=1}^{n}P(B_{i})P(A|B_{i}) P(A)=i=1∑nP(Bi)P(A∣Bi)
所以根据条件概率的公式和全概率公式,可以得到贝叶斯公式:
P ( B i ∣ A ) = P ( A B i ) P ( A ) = P ( B i ) P ( A ∣ B i ) ∑ P ( B i ) P ( A ∣ B i ) P(B_i|A)= \frac{P(AB_i)}{P(A)}=\frac{P(B_i)P(A|B_i)}{\sum P(B_i)P(A|B_i)} P(Bi∣A)=P(A)P(ABi)=∑P(Bi)P(A∣Bi)P(Bi)P(A∣Bi)
贝叶斯公式是建立在条件概率的基础上,寻找事情发生的原因。
先验概率与后验概率
以事件A为例,在上面提到的全概率公式 P ( A ) P(A) P(A) 就称为先验概率(Prior probability),即在事件 B 发生之间我们对事件 A 的概率有一个判断。 P ( A ∣ B ) P(A|B) P(A∣B) 称为后验概率(Posterior probability),即在事件 B 发生以后我们对事件 A 的发生概率有了一个新的估计。
假如在编号为 1,2 盒子里各有 10 个球, A 中有 4红,6白,B 中有 2红,8白。现从它们之中随机取一个球是红色的球,问这个球从编号 1 盒子中取得概率是多少?
设取出红球的事件为 B,从编号 1 盒子中抽球的事件为 A,所以从 A 盒子中取出一个球并且 是红球的概率可以表示为 P ( B ∣ A ) P(B|A) P(B∣A):
P ( B ) = 6 / 20 , P ( A ) = 10 / 20 , P ( B ∣ A ) = 4 / 10 P(B)=6/20,P(A)= 10/20 , P(B|A)= 4/ 10 P(B)=6/20,P(A)=10/20,P(B∣A)=4/10
根据贝叶斯公式可以得到:
P ( A ∣ B ) = P ( A ) P ( B ∣ A ) P ( B ) = ( 10 / 20 ) ∗ ( 4 ∗ 10 ) 6 / 20 = 2 3 P(A|B)= \frac{P(A)P(B|A)}{P(B)}= \frac{(10/20)*(4*10)}{6/20}=\frac{2}{3} P(A∣B)=P(B)P(A)P(B∣A)=6/20(10/20)∗(4∗10)=32
可以看到在事件 B 发生之间从 A 盒子中取球的先验概率为 1 2 \frac{1}{2} 21,当事件 B 发生以后 A 的后验概率就变成了 2 3 \frac{2}{3} 32 。
信息熵
信息本身是一个很抽象的概念,但是信息论之父香农在 1948 年的论文中借鉴了热力学中“熵(entropie)”的概念,提出了信息熵。在热力学中,熵是表示体系的混乱程度,体系越混乱,熵就越大。对应到信息论中,熵(信息熵)表示信息量的多少(不确定程度) ,熵越大,不确定性就越大,而不确定性大,代表事情发生的概率小,所以不确定性是概率的减函数。
我们知道,当事件A与事件B相对独立的时候,事件A,B 一起发生的概率为: P ( A , B ) = P ( A ) P ( B ) P(A,B)=P(A)P(B) P(A,B)=P(A)P(B)
而对于两个独立事件的不确定性应该满足可加性,设不确定性函数 f ( x ) f(x) f(x) 为: f ( A , B ) = f ( A ) + f ( B ) f(A,B)=f(A)+f(B) f(A,B)=f(A)+f(B)
首先将两个数相乘转换称两个数相加的关系,很显然,我们可以借助对数函数的性质,又因为两个是负相关,所以前面再加一个负号,这样我们就可以得到不确定性的计算表达式:
f ( p ) = l o g 1 p = − l o g p f(p)=log \frac{1}{p}= - log p f(p)=logp1=−logp
上面的式子是单个事件的不确定性,由 n 个事件共同组成的样本空间 U U U 的不确定性应当为单个事件的统计平均值 E E E,这就是信息熵,可以得到它的数学表达式为:
H ( U ) = E [ − l o g p ] = − ∑ i = 1 n p i l o g p i H(U)= E[-logp]= - \sum_{i=1}^{n} p_i log p_i H(U)=E[−logp]=−i=1∑npilogpi
上式中 log 以 2 为底单位为比特(bit),也可以以 e 为底,这时单位为纳特(nat)。
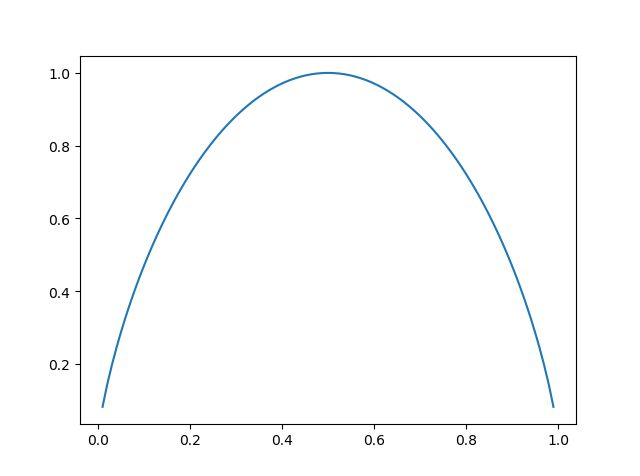
以二分类问题为例,设事件 A 与 事件 B 发生的概率分别为 p p p 和 1 − p 1-p 1−p,根据信息熵的定义:
H ( U ) = − p l o g p − ( 1 − p ) l o g ( 1 − p ) H(U)=-plogp-(1-p)log(1-p) H(U)=−plogp−(1−p)log(1−p)
H ( U ) H(U) H(U) 的曲线如下:
互信息
由上面的概率公式变换一下,可以得到:
P ( A , B ) = P ( A ∣ B ) P ( B ) = P ( B ∣ A ) P ( A ) P(A,B)=P(A|B)P(B)=P(B|A)P(A) P(A,B)=P(A∣B)P(B)=P(B∣A)P(A)
根据不确定函数对于概率的关系可得熵有如下关系:
H ( A , B ) = H ( A ∣ B ) + H ( B ) = H ( B ∣ A ) + H ( A ) H(A,B)=H(A|B)+H(B)=H(B|A)+H(A) H(A,B)=H(A∣B)+H(B)=H(B∣A)+H(A)
因此,由公式(6)可以得到:
I ( A ; B ) = H ( A ) − H ( A ∣ B ) = H ( B ) − H ( B ∣ A ) I(A;B)=H(A)-H(A|B)=H(B)-H(B|A) I(A;B)=H(A)−H(A∣B)=H(B)−H(B∣A)
这个差就叫做 A 和 B 的互信息,我们记作 I ( A ; B ) I(A;B) I(A;B) ,按照熵的定义,互信息的展开式为:
I ( A ; B ) = H ( A ) − H ( A ∣ B ) = H ( A ) + H ( B ) − H ( A , B ) = − ∑ x p ( x ) l o g p ( x ) − ∑ y p ( y ) l o g p ( y ) + ∑ x , y p ( x , y ) l o g p ( x , y ) = ∑ x , y p ( x , y ) l o g p ( x , y ) p ( x ) p ( y ) I\left ( A;B\right )=H\left ( A \right )-H\left ( A|B \right ) \\ = H\left ( A \right ) + H\left ( B \right ) -H\left ( A,B \right ) \\ = - \sum_{x} p(x)logp(x)-\sum_{y} p(y)logp(y)+\sum_{x,y}p(x,y)logp(x,y)\\ = \sum_{x,y} p(x,y)log \frac{p(x,y)}{p(x)p(y)} I(A;B)=H(A)−H(A∣B)=H(A)+H(B)−H(A,B)=−∑xp(x)logp(x)−∑yp(y)logp(y)+∑x,yp(x,y)logp(x,y)=∑x,yp(x,y)logp(x)p(y)p(x,y)
互信息表示的是事件之间在不确定性熵相互影响的程度。
条件熵
由公式(6)可以得到:
H ( A , B ) = H ( A ∣ B ) + H ( B ) = H ( B ∣ A ) + H ( A ) H(A,B)=H(A|B)+H(B)=H(B|A)+H(A) H(A,B)=H(A∣B)+H(B)=H(B∣A)+H(A)
这里的条件熵就是 H ( A ∣ B ) H(A|B) H(A∣B) 或者是 H ( B ∣ A ) H(B|A) H(B∣A)。根据上面的公式可以得到条件熵的表达式为:
H ( A ∣ B ) = H ( A , B ) − H ( B ) H(A|B)=H(A,B)-H(B) H(A∣B)=H(A,B)−H(B)
即 (A,B) 发生所包含的熵,减去 B 单独发生包含的熵,就是表示在 B 发生的前提下,A 发生时带来的熵。
H ( A , B ) − H ( B ) = − ∑ x , y p ( x , y ) l o g p ( x , y ) + ∑ y p ( y ) l o g p ( y ) = − ∑ x , y p ( x , y ) l o g p ( x , y ) + ∑ y ( ∑ x p ( x , y ) ) l o g p ( y ) = − ∑ x , y p ( x , y ) l o g p ( x , y ) + ∑ x , y p ( x , y ) l o g p ( y ) = − ∑ x , y p ( x , y ) l o g p ( x , y ) p ( y ) = − ∑ x , y p ( x , y ) l o g p ( x ∣ y ) H\left ( A,B \right )-H\left ( B \right ) \\ = - \sum_{x,y} p(x,y)logp(x,y)+\sum_{y}p(y)logp(y)\\ = - \sum_{x,y} p(x,y)logp(x,y)+\sum_{y} \left ( \sum_{x}p(x,y)\right ) logp(y) \\ = - \sum_{x,y} p(x,y)logp(x,y)+\sum_{x,y} p(x,y)logp(y)\\ = - \sum_{x,y} p(x,y)log \frac{p(x,y)}{p(y)}\\ = - \sum_{x,y} p(x,y)log p(x|y) H(A,B)−H(B)=−∑x,yp(x,y)logp(x,y)+∑yp(y)logp(y)=−∑x,yp(x,y)logp(x,y)+∑y(∑xp(x,y))logp(y)=−∑x,yp(x,y)logp(x,y)+∑x,yp(x,y)logp(y)=−∑x,yp(x,y)logp(y)p(x,y)=−∑x,yp(x,y)logp(x∣y)
再由上面公式进一步推导可得:
H ( A , B ) − H ( B ) = − ∑ x , y p ( x , y ) l o g p ( x ∣ y ) = − ∑ x ∑ y p ( y ) p ( x ∣ y ) l o g p ( x ∣ y ) = ∑ y p ( y ) ( − ∑ x p ( x ∣ y ) l o g p ( x ∣ y ) ) = ∑ y p ( y ) H ( X ∣ Y = y ) H\left ( A,B \right )-H\left ( B \right ) \\ = - \sum_{x,y} p(x,y)log p(x|y) \\ = - \sum_{x}\sum_{y}p(y)p(x|y)logp(x|y) \\ = \sum_{y} p(y)\left ( - \sum_{x}p(x|y)logp(x|y) \right )\\ = \sum_{y}p(y)H(X|Y=y) H(A,B)−H(B)=−∑x,yp(x,y)logp(x∣y)=−∑x∑yp(y)p(x∣y)logp(x∣y)=∑yp(y)(−∑xp(x∣y)logp(x∣y))=∑yp(y)H(X∣Y=y)
决策树
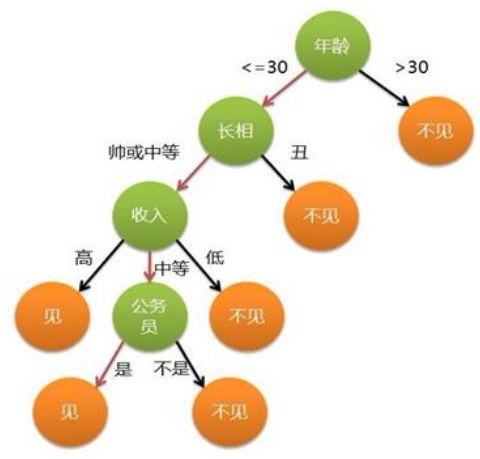
这里给出一个选择见还是不见相亲对象的决策树示意图,通过对判别标准一个个的进行比较,最终导致两个结果:见 或者 不见。首先决策树是一种树形结构(不全是二叉树),其中每个内部节点表示在一个属性上的测试,每个分支都代表一个测试输出,每个叶节点都代表一种类别,决策树是以实例为基础的归纳学习。 决策树学习采用的是自顶向下的递归方法,基本思想是以信息熵为度量构造一棵熵值下降最快的树,到叶子节点处的熵为 0,此时每个叶节点中的实例都属于同一类。很显然,决策树属于有监督学习。
信息增益
根据前面数学基础部分的熵与条件熵的概念得到的熵分别为 经验熵 和 经验条件熵。假设特征 A A A 对训练数据集 D D D 的信息增益为 g ( D , A ) g(D,A) g(D,A),而这里的信息增益 g ( D , A ) g(D,A) g(D,A) 就是指经验熵 H ( D ) H(D) H(D)与经验条件熵 H ( D ∣ A ) H(D|A) H(D∣A)之差:
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A)=H(D)-H(D|A) g(D,A)=H(D)−H(D∣A)
信息增益表示得知特征 A A A 的信息使得类 X 的信息的不确定性减少的程度,即为训练集 D D D 和特征 A 的互信息。
这里用李航博士《统计学习方法》中的例子来帮助理解:
这里将上述表格的信息进行一个归纳总结,总共有 4 个特征,然后每个特征对应最后的类别为 是/否 :
| 特征 | 分布 |
|---|---|
| A1 年龄 | { 5青年 : [2是 3否] } { 5中年 : [ 3是 2否 ] } { 5老年 : [ 4是 1否 ] } |
| A2 工作 | { 10没有工作 : [ 4是 6否 ] } { 5有工作 : [ 5是 ] } |
| A3 有房子 | {9没有房子 : [ 3是 6否 ] } { 6有房子 : [ 6是 ] } |
| A4 信贷 | { 6好 : [4是 2否] } { 5一般 : [ 1是 4否 ] } { 4非常好 : [ 4是 ] } |
| 类别 D | 9 是 6 否 |
以其中一个归纳举例,{ 5青年 : [2是 3否] } 表示 A1年龄 这个特征中 有 5 个是青年,5个青年中有 2 个批准申请贷款,3个不批准申请贷款,依次类推。
根据上面的定义式:
经验熵 H ( D ) H(D) H(D):
H ( D ) = − 9 15 l o g 2 9 15 − 6 15 l o g 2 6 15 = 0.971 H(D)= - \frac{9}{15}log_2 \frac{9}{15}- \frac{6}{15}log_2 \frac{6}{15}=0.971 H(D)=−159log2159−156log2156=0.971
因为其中 类别 D 有 9 个是批准,6个不批准。
条件经验熵 H ( D ∣ A 1 ) H(D|A^1) H(D∣A1):
最后求得 H ( D ∣ A 1 ) = 0.888 H(D|A^1)= 0.888 H(D∣A1)=0.888 。
这里得 D1,D2,D3,分别对应 青年,中年,老年,括号里的概率分别对应青年,中年,老年中的 是 和 否 的个数。
依次类推可以计算得到 H ( D ∣ A 2 ) H(D|A^2) H(D∣A2), H ( D ∣ A 3 ) H(D|A^3) H(D∣A3), H ( D ∣ A 4 ) H(D|A^4) H(D∣A4)。
信息增益 g ( D , A 1 ) g(D,A^1) g(D,A1):
根据定义式可得:
g ( D , A 1 ) = H ( D ) − H ( D ∣ A 1 ) = 0.971 − 0.888 = 0.083 g(D,A^1)=H(D)-H(D|A^1)=0.971-0.888=0.083 g(D,A1)=H(D)−H(D∣A1)=0.971−0.888=0.083
同理可得:
g ( D , A 2 ) = H ( D ) − H ( D ∣ A 2 ) = 0.971 − 0.647 = 0.324 g(D,A^2)=H(D)-H(D|A^2)=0.971-0.647=0.324 g(D,A2)=H(D)−H(D∣A2)=0.971−0.647=0.324
g ( D , A 3 ) = H ( D ) − H ( D ∣ A 3 ) = 0.971 − 0.551 = 0.420 g(D,A^3)=H(D)-H(D|A^3)=0.971-0.551=0.420 g(D,A3)=H(D)−H(D∣A3)=0.971−0.551=0.420
g ( D , A 4 ) = H ( D ) − H ( D ∣ A 4 ) = 0.971 − 0.608 = 0.363 g(D,A^4)=H(D)-H(D|A^4)=0.971-0.608=0.363 g(D,A4)=H(D)−H(D∣A4)=0.971−0.608=0.363
信息增益率
知道信息增益的概念后,这里直接给出信息增益率的定义式:
g r ( D , A ) = g ( D , A ) H ( A ) g_{r}(D,A)= \frac{g(D,A)}{H(A)} gr(D,A)=H(A)g(D,A)
继续上面的例子:
特征 A 1 A^1 A1 中有 5 个青年,5个中年,5个老年, A 2 A^2 A2 中 10 个没有工作,5个有工作,同理 A 3 A^3 A3, A 4 A^4 A4 可得:
H ( A 1 ) = − 5 15 l o g 2 5 15 − 5 15 l o g 2 5 15 − 5 15 l o g 2 5 15 = 1.585 H(A^1)=- \frac{5}{15}log_2\frac{5}{15}- \frac{5}{15}log_2\frac{5}{15}- \frac{5}{15}log_2\frac{5}{15}=1.585 H(A1)=−155log2155−155log2155−155log2155=1.585 H ( A 2 ) = − 10 15 l o g 2 10 15 − 5 15 l o g 2 5 15 = 0.918 H(A^2)=- \frac{10}{15}log_2\frac{10}{15}- \frac{5}{15}log_2\frac{5}{15}=0.918 H(A2)=−1510log21510−155log2155=0.918 H ( A 3 ) = − 9 15 l o g 2 9 15 − 6 15 l o g 2 6 15 = 0.971 H(A^3)=- \frac{9}{15}log_2\frac{9}{15}- \frac{6}{15}log_2\frac{6}{15}=0.971 H(A3)=−159log2159−156log2156=0.971 H ( A 4 ) = − 6 15 l o g 2 6 15 − 5 15 l o g 2 5 15 − 4 15 l o g 2 4 15 = 1.565 H(A^4)=- \frac{6}{15}log_2\frac{6}{15}- \frac{5}{15}log_2\frac{5}{15}-\frac{4}{15}log_2\frac{4}{15}=1.565 H(A4)=−156log2156−155log2155−154log2154=1.565
所以上面的信息增益为:
g r ( D , A 1 ) = 0.083 1.585 = 0.052 g_r(D,A^1)= \frac{0.083}{1.585}=0.052 gr(D,A1)=1.5850.083=0.052 g r ( D , A 2 ) = 0.324 0.918 = 0.353 g_r(D,A^2)= \frac{0.324}{0.918}=0.353 gr(D,A2)=0.9180.324=0.353 g r ( D , A 3 ) = 0.420 0.971 = 0.432 g_r(D,A^3)= \frac{0.420}{0.971}=0.432 gr(D,A3)=0.9710.420=0.432 g r ( D , A 4 ) = 0.363 1.565 = 0.232 g_r(D,A^4)= \frac{0.363}{1.565}=0.232 gr(D,A4)=1.5650.363=0.232
基尼系数
对于分类问题,假设有 K 类,属于第 k 类的概率为 p k p_{k} pk,则概率分布的基尼系数为:
G i n i ( p ) = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 Gini(p)=\sum_{k=1}^{K}p_{k}(1-p_{k})=1- \sum_{k=1}^{K}p_{k}^2 Gini(p)=k=1∑Kpk(1−pk)=1−k=1∑Kpk2
如果样本集合 D D D 根据特征 A A A 是否取某一个值 a 被分割成 D 1 D_1 D1, D 2 D_2 D2两部分,则在特征 A A A 的条件下,集合 D D D 的基尼系数定义为:
G i n i ( D , A ) = ∣ D 1 ∣ D G i n i ( D 1 ) + ∣ D 2 ∣ D G i n i ( D 2 ) Gini(D,A)= \frac{|D_1|}{D}Gini(D_1)+\frac{|D_2|}{D}Gini(D_2) Gini(D,A)=D∣D1∣Gini(D1)+D∣D2∣Gini(D2)
基尼指数 G i n i ( D ) Gini(D) Gini(D) 表示集合 D D D 的不确定性, G i n i ( D , A ) Gini(D,A) Gini(D,A) 表示经 A = a A=a A=a 分割后集合 D D D 的不确定性。基尼指数值越大,样本集合的不确定性就越大,与熵相似。
以上述题目为例,年龄特征 A 1 A^1 A1 :青年,中年,老年 会分别划分为:
Gini(D,A1 = 1) 对应 D1 = 青年,D2 = 中年,老年
Gini(D,A1 = 2) 对应 D1 = 中年,D2 = 青年,老年
Gini(D,A1 = 3) 对应 D1 = 老年,D2 = 青年,中年
依次类推。 ∣ D i ∣ |D_i| ∣Di∣ 指对应类别的样本总数, ∣ D ∣ |D| ∣D∣ 表示集合总样本数。
H ( D ∣ A 1 ) = 5 15 ( 2 × 2 5 × ( 1 − 2 5 ) ) + 10 15 ( 2 × 7 10 × ( 1 − 7 10 ) ) = 0.44 H(D|A^1)= \frac{5}{15} \left( 2 \times \frac{2}{5} \times \left(1-\frac{2}{5} \right) \right)+ \frac{10}{15} \left( 2 \times \frac{7}{10} \times \left(1-\frac{7}{10} \right) \right)=0.44 H(D∣A1)=155(2×52×(1−52))+1510(2×107×(1−107))=0.44
依次类推:
G i n i ( D , A 1 ) Gini(D,A^1) Gini(D,A1)
G i n i ( D , A 1 = 1 ) = 0.44 Gini(D,A^1 = 1) = 0.44 Gini(D,A1=1)=0.44 #青年
G i n i ( D , A 1 = 2 ) = 0.48 Gini(D,A^1 = 2) = 0.48 Gini(D,A1=2)=0.48 #中年
G i n i ( D , A 1 = 3 ) = 0.44 Gini(D,A^1 = 3) = 0.44 Gini(D,A1=3)=0.44 #老年
G i n i ( D , A 2 ) Gini(D,A^2) Gini(D,A2)
G i n i ( D , A 2 = 1 ) = 0.32 Gini(D,A^2 = 1) = 0.32 Gini(D,A2=1)=0.32
G i n i ( D , A 3 ) Gini(D,A^3) Gini(D,A3)
G i n i ( D , A 3 = 1 ) = 0.27 Gini(D,A^3 = 1) = 0.27 Gini(D,A3=1)=0.27 # 所有基尼指数中的最小值
G i n i ( D , A 4 ) Gini(D,A^4) Gini(D,A4)
G i n i ( D , A 4 = 1 ) = 0.36 Gini(D,A^4 = 1) = 0.36 Gini(D,A4=1)=0.36
G i n i ( D , A 4 = 2 ) = 0.47 Gini(D,A^4 = 2) = 0.47 Gini(D,A4=2)=0.47
G i n i ( D , A 4 = 3 ) = 0.32 Gini(D,A^4 = 3) = 0.32 Gini(D,A4=3)=0.32
基尼指数主要是用来选择 最优特征 和 最优切分点 的。
决策树生成
经过上面一些概念的讲解,下面3种决策树生成树生成算法就不难理解了,主要来看一下他们的区别:
- ID3 : 使用信息增益(互信息) g ( D , A ) g(D,A) g(D,A)来进行特征选择 (信息增益最大化)
- C4.5 :使用的是信息增益率 g r ( D , A ) g_r(D,A) gr(D,A) 来进行特征选择 (信息增益率最大化)
- CART : 使用基尼指数 G i n i ( D , A ) Gini(D,A) Gini(D,A) 来进行特征选择 (基尼指数最小化),上面 G i n i ( D , A 3 = 1 ) = 0.27 Gini(D,A^3 = 1) = 0.27 Gini(D,A3=1)=0.27 是最小的,所以 A 3 A^3 A3 是最佳分割特征, A 3 = 1 A^3=1 A3=1 是最佳分割点
决策树剪枝
在 ID3 算法中是没有剪枝操作的,所以这种方法容易出现过拟合,在 C4.5 中加入了剪枝操作,主要是在决策树学习的损失函数中加入了叶节点个数的考虑,将其作为惩罚项,自下而上递归地将叶节点回缩以后计算损失函数,损失函数值变小,则删除当前节点。
CART 是指分类与回归树,其首先从生成算法生成的树底端不断剪枝,直到根节点,形成一个子树序列,然后通过验证法计算每一个子树的损失函数,从中选择最优的子树。
Bagging 与 随机森林
Bagging
Bootstraping 方法又称自助法,是有放回的抽样方法,基于这种方法我们将介绍 Bagging 方法的思路:
- 从样本集中有放回的重采样,每次选出 n 个样本
- 在所有属性上,对这 n 个样本建立分类器(ID3,C4.5,CART,SVM,Logistic 回归等)
- 重复以上两步 m 次,获得 m 个分类器
- 将数据放在这 m 个分类器上,最后根据这 m 个分类器的投票结果,决定数据属于哪一类
随机森林
而 随机森林方法是在 bagging 方法上做了修改:
- 从样本集中有放回的重采样,每次选出 n 个样本
- 从所有属性中随机选择 k 个属性,选择最佳分割作为节点建立 CART 决策树
- 重复以上两步 m 次,获得 m 个 CART 决策树
- 这 m 个 CART 决策树形成随机森林,通过投票,决定数据属于哪一类
因为随机森林在选取的时候充满随机性,所以基本是不可复线的,即同样的参数下跑的分类结果可能存在略微差异,但大体相似。
参考文献:
https://baike.baidu.com/item/信息熵/7302318
https://blog.csdn.net/weixin_34370347/article/details/87143933