二叉平衡树(Java)
在学习了 二叉排序树 的基础上,继续结合TreeMap的源码实现了二叉平衡树。
性质
平衡二叉搜索树(Balanced Binary Tree)具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。常用算法有红黑树、AVL、Treap、伸展树等。在平衡二叉搜索树中,我们可以看到,其高度一般都良好地维持在O(log2n),大大降低了操作的时间复杂度。
实现算法
1. 左旋LL
2. 右旋RR
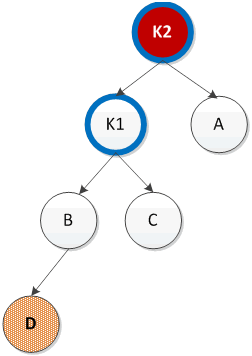
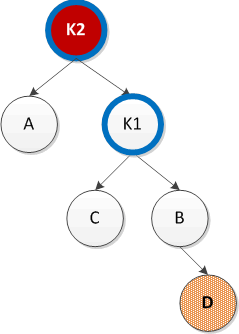
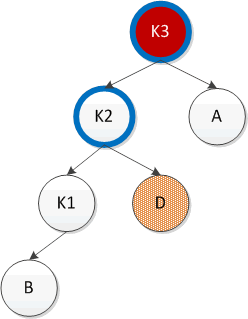
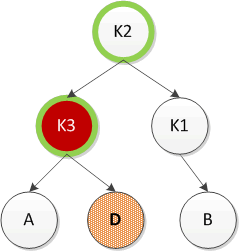
3. 先左旋后右旋LR
4. 先右旋后左旋RL
代码实现
package com.xqq.二叉平衡树;
import java.util.Stack;
public class AVLTree {
private Entry root;
private int size = 0;
public AVLTree() {
}
public AVLTree(E [] values) {
for(E value : values){
insert(value);
}
}
public int size() {
return size;
}
public boolean contains(E value) {
return (getEntry(value) != null);
}
@SuppressWarnings("unchecked")
public Entry getEntry(E value) {
Entry t = root;
Comparable v = (Comparable) value;
while (t != null) {
int cmp = v.compareTo(t.value);
if (cmp < 0) {
t = t.left;
} else if (cmp > 0) {
t = t.right;
} else {
return t;
}
}
return null;
}
/**
* 首先找到插入位置
*/
@SuppressWarnings("unchecked")
public boolean insert(E value) {
Entry t = root;
if (t == null) {
root = new Entry(value, null);
size = 1;
return true;
}
Entry parent;// 保存父节点
int cmp;
Comparable v = (Comparable) value;
// 从根节点向下搜索,找到插入位置
do {
parent = t;
cmp = v.compareTo(t.value);
if (cmp < 0) {
t = t.left;
} else if (cmp > 0) {
t = t.right;
} else {
return false;
}
} while (t != null);
Entry child = new Entry(value, parent);
if(cmp < 0){
parent.left = child;
}else {
parent.right = child;
}
//检查是否平衡
fixAfterInsertion(child);
size ++;
return true;
}
/**
* 左旋
*
* 1)把节点C的左子树作为节点A的右子树
* 2)把节点C代替节点A
* 3)把节点A做为节点C的左子树
* 1 A C
* / \ / \
* 2 B C A E
* / \ -> / \ \
* 3 D E B D F
* \
* 4 F
*
* 节点A破坏了平衡
*/
private void rotateLeft(Entry p){
System.out.println("绕 " + p.value + " 左旋");
if(p != null){
Entry r = p.right;
p.right = r.left;
if(r.left != null)
r.left.parent = p;
r.parent = p.parent;
if(p.parent == null)
root = r;
else if(p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
r.left = p;
p.parent = r;
}
}
/**
* 右旋:
* 1)将B的右孩子作为A的左孩子
* 2)将B代替A的位置
* 3)将A作为B的右孩子
*
* 1 A B
* / \ / \
* 2 B C D A
* / \ -> / / \
* 3 D E F E C
* /
* 4 F
*
* 节点A破坏了平衡
*/
private void rotateRight(Entry p){
System.out.println("绕 " + p.value + " 右旋");
if(p != null){
Entry l = p.left;
p.left = l.right; //让节点B的右子树作为节点A的左子树
if(l.right != null)
l.right.parent = p; //如果节点B的右子树非空,则让右子树的父亲节点A
l.parent = p.parent; //节点B的父亲指向节点A的父亲
if(p.parent == null)
root = l; //如果节点A为根节点,则将节点B置为根节点
else if(p.parent.left == p)
p.parent.left = l; //如果节点A为其父亲节点的左孩子,则将节点B置为左孩子
else
p.parent.right = l; //否则置为右孩子
l.right = p; //将节点A置为节点B的右孩子
p.parent = l;
}
}
/**
* 插入后检查是否破坏平衡,如果破坏,进行旋转
*
* 调整的方法:
* 1.当最小不平衡子树的根(以下简称R)为2时,即左子树高于右子树:
* 如果R的左子树的根节点的BF为1时,做右旋;
* 如果R的左子树的根节点的BF为-1时,先左旋然后再右旋
*
* 2.R为-2时,即右子树高于左子树:
* 如果R的右子树的根节点的BF为1时,先右旋后左旋
* 如果R的右子树的根节点的BF为-1时,做左旋
*/
private void fixAfterInsertion(Entry e) {
Entry parent = getNotBalance(e);
if(parent != null){
if(parent.balance == 2)
leftBalance(parent);
else
rightBalance(parent);
}
}
/**
* 进行左平衡
* 情况1:
* A B
* / \ / \
* B C 左旋 D A
* / \ -------> / / \
* D E F E C
* /
* F
*
* 情况2:
* A A E
* / \ / \ / \
* B C 先左旋 E C 再右旋 B A
* / \ -------> / ------> / \ \
* D E B D F C
* / / \
* F D F
* 情况3:
* A A E
* / \ / \ / \
* B C 先左旋 E C 再右旋 B A
* / \ -------> / \ ------> / / \
* D E B F D F C
* \ /
* F D
* 情况4:
* A B
* / \ / \
* B C 左旋 D A
* / \ -------> / / \
* D E F E C
* / / /
* F G G
*/
private void leftBalance(Entry p) {
Entry l = p.left;
switch (l.balance) {
case LH: //左高,右旋调整,旋转后树的高度减小,情况1
p.balance = l.balance = EH;
rotateRight(p);
break;
case RH: //右高,分情况讨论
Entry lr = l.right;
switch (lr.balance) {
case LH: //情况2
p.balance = RH;
l.balance = EH;
break;
case RH: //情况3
l.balance = LH;
p.balance = EH;
break;
case EH: //删除时才会出现此种情况
p.balance = l.balance = EH;
break;
}
lr.balance = EH;
rotateLeft(l);
rotateRight(p);
break;
case EH: //特殊情况4,这种情况在添加时不可能出现,只在移除时可能出现,旋转之后整体树高不变
p.balance = LH;
l.balance = RH;
rotateRight(p);
break;
}
}
/**
* 进行右平衡
* 情况1:
* A C
* / \ / \
* B C 左旋 A E
* / \ -------> / \ \
* D E B D F
* \
* F
* 情况2:
* A A D
* / \ / \ / \
* B C 先右旋 B D 再左旋 A C
* / \ -------> / \ ------> / \ \
* D E F C B F E
* / \
* F E
*
* 情况3:
* A A D
* / \ / \ / \
* B C 先右旋 B D 再左旋 A C
* / \ -------> \ ------> / / \
* D E C B F E
* \ / \
* F F E
* 情况4:
* A C
* / \ / \
* B C 左旋 A E
* / \ -------> / \ /
* D E B D G
* / / /
* F G F
*/
private void rightBalance(Entry p) {
Entry r = p.right;
switch (r.balance) {
case RH: //右高,直接左旋 情况1
p.balance = r.balance = EH;
rotateLeft(p);
break;
case LH: //左高,分情况讨论
Entry rl = r.left;
switch (rl.balance) {
case LH:
p.balance = EH;
r.balance = RH;
break;
case RH:
p.balance = LH;
r.balance = EH;
break;
case EH:
p.balance = r.balance = EH;
break;
}
rl.balance = EH;
rotateRight(r);
rotateLeft(p);
break;
case EH:
p.balance = RH;
r.balance = LH;
rotateLeft(p);
break;
}
}
/**
* 获取不平衡的节点
*/
private Entry getNotBalance(Entry e) {
Entry parent = e.parent;
@SuppressWarnings("unchecked")
Comparable ec = (Comparable) e.value;
while(parent != null){
int cmp = ec.compareTo(parent.value);
if(cmp < 0){
parent.balance ++;
}else{
parent.balance --;
}
if(parent.balance == 0)
break;
if(Math.abs(parent.balance) == 2)
return parent;
parent = parent.parent;
}
return null;
}
/**
* 非递归:中序遍历
*/
public void inOrderUnRecur(){
System.out.print("非递归中序遍历: ");
if(root == null) return ;
Entry t = root;
Stack> stack = new Stack>();
while(!stack.isEmpty() || t != null){
if(t != null){
stack.push(t);
t = t.left;
}else {
t = stack.pop();
System.out.print(t.value + " ");
t = t.right;
}
}
System.out.println();
}
public boolean remove(E value){
Entry e = getEntry(value);
if(e != null){
deleteEntry(e);
return true;
}
return false;
}
private void deleteEntry(Entry p) {
size--;
// 如果左右子树均存在 ,找到其直接后继,替换p,之后p指向s,删除p实际是删除s
// 所有的删除左右子树不为空的节点都可以调整为删除左右子树有其一不为空,或都为空的情况。
if(p.left != null && p.right != null){
Entry s = successor(p);
p.value = s.value;
p = s;
}
Entry replacement = (p.left != null ? p.left : p.right);
if(replacement != null){ //如果其左右子树有一个不为空
replacement.parent = p.parent;
if(p.parent == null){ //如果为根节点
root = replacement;
}else if(p.parent.left == p){ //如果为左孩子
p.parent.left = replacement;
}else{
p.parent.right = replacement;//为右孩子
}
p.left = p.right = p.parent = null; //p的指针清空
//这里更改了replacement的父节点,所以可以直接从它开始向上回溯
fixAfterDeletion(replacement);
}else if(p.parent == null){ // 如果只有一个节点
root = null;
}else{ // 如果为叶子节点
fixAfterDeletion(p);//直接从该叶子节点回溯
if(p.parent.left == p){
p.parent.left = null;
}else {
p.parent.right = null;
}
p.parent = null;
}
}
/**
* 删除某节点p后的调整方法:
* 1.从p开始向上回溯,修改祖先的BF值,这里只要调整从p的父节点到根节点的BF值,
* 调整原则为,当p位于某祖先节点(简称A)的左子树中时,A的BF减1,当p位于A的
* 右子树中时A的BF加1。当某个祖先节点BF变为1或-1时停止回溯,这里与插入是相反的,
* 因为原本这个节点是平衡的,删除它的子树的某个节点并不会改变它的高度
*
* 2.检查每个节点的BF值,如果为2或-2需要进行旋转调整,调整方法如下文,
* 如果调整之后这个最小子树的高度降低了,那么必须继续从这个最小子树的根节点(假设为B)继续
* 向上回溯,这里和插入不一样,因为B的父节点的平衡性因为其子树B的高度的改变而发生了改变,
* 那么就可能需要调整,所以删除可能进行多次的调整。
*/
@SuppressWarnings("unchecked")
private void fixAfterDeletion(Entry p) {
Entry t = p.parent;
Comparable e = (Comparable) p.value;
while(t != null){
int cmp = e.compareTo(t.value);
if(cmp < 0){
t.balance ++;
}else {
t.balance --;
}
if(Math.abs(t.balance) == 1){ //父节点经过调整平衡因子后,如果为1或-1,说明调整之前是0,停止回溯。
break;
}
Entry r = t;
if(t.balance == 2){
leftBalance(r);
}else if(t.balance == -2){
rightBalance(r);
}
t = t.parent;
}
}
/**
* 找到p节点的直接后继节点
*/
private Entry successor(Entry p) {
if(p == null)
return null;
else if(p.right != null){ //找到其右孩子,往左走到尽头
Entry r = p.right;
while(r.left != null){
r = r.left;
}
return r;
}
return null;
}
private static final int LH = 1; //左高
private static final int EH = 0; //等高
private static final int RH = -1; //右高
static class Entry {
E value;
Entry left;
Entry right;
Entry parent;
int balance = EH; //平衡因子,只能为-1、0或者1,否则需要旋转
public Entry(E value, Entry parent) {
this.value = value;
this.parent = parent;
}
}
}
测试代码:
package com.xqq.二叉平衡树;
public class Test {
public static void main(String[] args) {
AVLTree avl = new AVLTree();
for(int i = 1; i < 100; i++){
avl.insert(i);
}
avl.inOrderUnRecur();
System.out.println(avl.remove(2));
avl.inOrderUnRecur();
}
} 参考:http://blog.csdn.net/zxman660/article/details/7940190