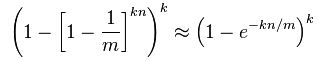深夜学算法之Bloom Filter：概率游戏

1. 前言

Bloom Filter的名字早有耳闻，但一直没看实现原理。今天乘地铁时心血来潮看了算法，顿时被其简单与优雅震惊。摘录下wiki上的介绍：

A Bloom filter is a space-efficient probabilistic data structure, conceived by Burton Howard Bloom in 1970, that is used to test whether an element is a member of a set.
Bloom Filter是一种高效利用空间的概率数据结构，由Burton Howard Bloom于1970年发明，用于检测一个元素是否属于一个集合。

讲个小插曲，我刚开始以为bloom作「开花，繁盛」解，没想到是发明人的名字，真相总是没有想象的美好呢…

我的实现：https://github.com/liquidconv/DSAF

2. 学习Bloom Filter

2.1 爬虫与集合操作

Bloom Filter通常和爬虫联系在一起，所以用这个例子解释其特性再好不过。爬虫最常用的抓取方法是广度优先搜索BFS，概括地说就是：

维护一个待访问链接的队列
每次将队首元素，即里第一个链接出队
将该链接对应的页面上所有链接入队
重复1~3至队列空为止

上面的描述里存在一个很大的问题——第三步里要加入队列的链接可能没有访问过，可能已经访问过，如果不做判断一律加入的话，一个相同的页面就可能被访问几千几万次，造成资源浪费。

要解决也很简单，只要维护一个访问过链接的集合就可以了。链接入队之前，先判断是否属于该集合，即是否已经访问过了，属于就不入队，不属于才入队。

2.2 思考

我们需要一个「集合」数据结构，至少要能够支持插入元素到集合和判断元素是否属于集合——也就是插入和属于这两种操作，要怎么实现呢？

可行思路：数组/链表/树/哈希表

暂时不考虑插入和查找操作的时间复杂度，上面每种做法里数据单元（数组的元素，链表和树的节点，哈希表的表项）定义形式基本都是：

typedef struct data_item {
    key k;     // 原始数据，或者原始数据的hash值等
    extra e ;  // 附加信息，指向其它节点的指针等
};

每次向集合插入元素都要生成新的data_item，空间复杂度是O(N)，大数据情况下hold不住。

算法里经常有时空权衡的问题，可以用空间换时间保存子问题结果，比如动态规划；可以用时间换空间，比如用泰勒展开计算三角函数。当时间和空间都不能牺牲的时候，就只能牺牲正确率了。Bloom Filter之所以称为概率数据结构，就是因为它的操作结果有一定概率是错误的。

2.3 图解Bloom Filter

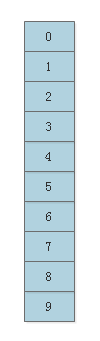
Bloom Filter的核心是一个m位的bitset和k个hash函数。

初始时bitset中所有位的值都设置为0，假设取m = 10，k = 3，用蓝色表示某位为0，红色表示为1：

初始化时的bitset

插入元素的过程是三步走：

计算k个hash值
将k个hash值对m取模得到k个下标
将bitset中k个下标对应的位设置为1

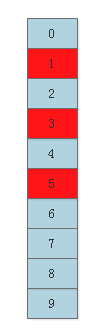
比如向刚才的Bloom Filter插入元素“Alice”。分别用3个hash函数计算“Alice”的hash值，将hash值对10取模，得到在[0, 10)范围内的r1、r2、r3，假设计算结果为：

r1 = h1("Alice") % m = 1
r2 = h2("Alice") % m = 3
r3 = h3("Alice") % m = 5

于是将bitset中第1位、第3位和第5位的值置为1：

第一次插入后的bitset

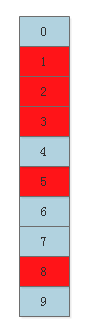
再插入元素“Bob”的过程还是一样的，假设：

r1 = h1("Bob") % m = 8
r2 = h2("Bob") % m = 2
r3 = h3("Bob") % m = 3

那就将bitset中第2位、第3位、第8位的值置为1（值已经为1的第3位不动）：

第二次插入后的bitset

图形化思考的话就是，Bloom Filter运行过程中不断插入新元素，bitset里的0逐渐被翻转成1。

怎么判断元素“Alice”是否在集合里呢？同样还是三步走：

计算k个hash值
将k个hash值对m取模得到k个下标
检查bitset中k个下标对应的位是否都为1

如果Bloom Filter里有“Alice”，那bitset中相应的k位值显然都为1。问题是即使Bloom Filter里没有“Alice”，还是可能由于之前插入的元素而导致“Alice”对应的k位值都为1，因此会错误地认为集合里已经有“Alice”了，这就是Bloom Filter会出错的地方。

由于bitset里每位都和多个元素有关，将某个为1的位置为0，涉及到这位的元素都会被认为不属于集合，所以Bloom Filter不支持删除操作。

2.4 复杂度分析

空间复杂度方面，Bloom Filter不会动态增长，运行过程中维护的始终只是m位的bitset，所以空间复杂度只有O(m)。

时间复杂度方面，Bloom Filter的插入与属于操作主要都是在计算k个hash，所以都是O(k)。

3. 实现Bloom Filter

3.1 定义Bloom Filter类

STL里的bitset定义时就要给定长度，而且之后不能改变，所以我用了vector。

#ifndef __BLOOM_FILTER_H__
#define __BLOOM_FILTER_H__

#include 
#include 

class BloomFilter {
    public:
        BloomFilter(unsigned int m, unsigned int k);
        void insertElement(std::string s);
        bool existsElement(std::string s);
    private:
        unsigned int BKDR_Hash(std::string s, unsigned int i);
        unsigned int getSeed(unsigned int hash_index);
        std::vector table;
        unsigned int _m;
        unsigned int _k;
};

#endif // __BLOOM_FILTER_H__

定义非常简单：

_m是bitset的大小，table是bitset
_k是hash函数的数量
BKDR_Hash是使用了参数seed的hash函数
用getSeed生成_k种seed，相当于有了_k种hash函数
insertElement对于插入操作
existsElement对应查找操作

构造函数

BloomFilter::BloomFilter(unsigned int m, unsigned int k):
    _m(m), _k(k) {
        table.resize(_m);
        for(int i = 0; i < _m; ++i)
            table[i] = false;
}

3.2 插入与属于

插入操作 = 计算_k个hash值，将table中对应位置改为true：

void BloomFilter::insertElement(string s) {
    for(int i = 0; i < _k; ++i) {
        unsigned int index = BKDR_Hash(s, i);
        table[index] = true;
    }
}

属于操作 = 计算_k个hash值，检查table中对应位置是否都为true：

bool BloomFilter::existsElement(string s) {
    for(int i = 0; i < _k; ++i) {
        unsigned int index = BKDR_Hash(s, i);
        if(!table[index])
            return false;
    }
    return true;
}

3.3 BKDR Hash

选择BKDR Hash最主要的原因就是有参数seed，很容易就能构造一族Hash函数。seed是个「魔数」（magic number），所以不用多纠结，推荐取的值为：
131,1313,13131,...

生成第hash_index个Hash函数的seed：

unsigned int BloomFilter::getSeed(unsigned int hash_index) {
    string seed = "13";
    for(int i = 0; i < hash_index; ++i)
        seed += (i % 2 == 0)? "1" : "3";

    return atoi(seed.c_str());
}

用第hash_index个Hash函数计算字符串s的hash值：

unsigned int BloomFilter::BKDR_Hash(string s, unsigned int hash_index) {
    const char *ps = s.c_str();
    unsigned int seed = getSeed(hash_index);
    unsigned int hash = 0;

    for(int i = 0; i < s.size(); ++i)
        hash += hash * seed + ps[i];

    return hash % _m;
}

4. 数学部分

Bloom Filter的原理已经讲完，但还是有必要提一下错误率的问题。错误率有两种：

FP = false positive
FN = false negative

对应Bloom Filter的情况下，FP就是「集合里没有某元素，查找结果是有该元素」，FN就是「集合里有某元素，查找结果是没有该元素」。FN显然总是0，FP会随着Bloom Filter中插入元素的数量而增加——极限情况就是所有bit都为1，这时任何元素都会被认为在集合里。

FP的推导并不复杂，wiki上有非常详细的过程，这里就简单地抄个结果，其中n是当前集合里元素的数量：

FP表达式，截自wiki

从这个公式里可以读出一些直观的信息：

n = 0时，FP = 0；n趋于无穷大时，FP趋于1
k/m和n保持不变时，k越大，FP越小

m和k决定了Bloom Filter的「容量」，当然hash函数的选择也很重要。

5. 参考资料

Bloom Filter
https://en.wikipedia.org/wiki/Bloom_filter
Precision and recall
https://en.wikipedia.org/wiki/Precision_and_recall
BloomFilter——大规模数据处理利器
http://www.cnblogs.com/heaad/archive/2011/01/02/1924195.html
各种Hash函数和代码
http://www.cppblog.com/bellgrade/archive/2009/09/29/97565.html