拼写错误检测(动态规划法)

最近忙于完成分布式数据库大项目的代码，算法作业也因此被搁置了好几天。分布式代码终于敲完交上去了，现在有时间继续完成算法作业了。其实算法作业并不是很难，大家仔细分析下问题，多搜搜博客，学习下前辈们如何解决这类问题，问题其实很容易解决的！只有站在前人的肩膀上，我们才能取得更大的进步，同时塑造更好的自己（不管了，我就是想写小学生作文~~~）！我还是本着原来的想法，我把我的思路和设计的关键部分贴出来，大家分享学习，全部的代码我不会放出来，原因很简单，我不是很想让大家都交雷同作业，也希望大家能理解。下面开始我们的第三个算法的设计与实现吧。

---

任务要求：以第2题中的哈希表英语词典为基础，应用动态规划法设计和实现拼写错误检测程序。 对输入单词进行检测，如果不正确，给出最接近的3个可选词。

---

算法思想：

首先我们要讲一个名词：编辑距离（EditDistance）【又称Levenshtein距离】：对于两个字符串，由一个转换为另一个所需的最少编辑操作次数。其中许可的编辑操作包括将一个字符替换成为另一个字符，插入一个字符，删除一个字符。

想了一个简单直观的例子，帮助大家理解以上两句话：

输入待查对象：kittain，我们字典中的一个对象sitting，我们求他俩的最短编辑距离的时候的步骤为：

sittain(k->s替换);

sittin(删掉a);

sitting(插入g)。

但是电脑毕竟不是人脑，它没有思想，它一眼看不出来我们上述的操作，但是它擅长搜索啊，计算啊。所以我们一个字母一个字母的开始做比较。

首先想我们算最终的编辑距离是不是得依赖前面算得的编辑距离，我们是不是得层层递归，才能算出从字符串a到字符串b的编辑距离，所以我们使用了分治的思想，将一个复杂的问题分解为类似的子问题。

所以我们先按照递归的思想：

字符串a，共m位，从a[1]到a[m]


字符串b，共n位，从b[1]到b[n]


d[i][j]表示字符串a到b的编辑距离。

按照递归的思想做解决这个问题（a[i]和b[j]为a,b的最后一位）：

<1>当a[i]=b[j],d[i][j] = d[i-1][j-1]


<2>当d[i]!=b[j],d[i][j]等于如下三项的最小值：


    ·d[i-1][j]+1(删除a[i])


    ·d[i][j-1]+1(插入b[j])


    ·d[i-1][j-1]+1(将a[i]替换成b[j])

递归的边界：

·a[i][0] = i,b字符串为空，表示将a[1]到a[i]全部删除，所以编辑距离为i；


·a[0][i] = j,a字符串为空，表示将b[1]到b[j]全部插入，所以编辑距离为j。

优化：（动态规划解决冗余）
以上的设计思路中存在着严重的问题，由于采用了递归，导致代码的效率很低下，时间复杂度呈指数增长，也存在这大量的重复字问题的计算，解决这种冗余的办法就是用动态规划。

递归的解决思路是从后往前算的，也就是我们想的到d[i][j],就必须先得到 d[i][j-1]、d[i-1][j]、d[i-1][j-1]三者中的最小。

而动态规划的思想恰恰相反，它的思想就是从前往后算，先算出各个子问题，然后根据子问题，计算得出原问题，因此可以解决大量出现的冗余问题。

设计思路：

首先，在第二题的代码中，我给出了一个find()函数，这个函数的作用是根据我所输入的待查找字符串，计算出hashCode，然后去我的哈希表里面查找这个字符串，如果存在的话，可以直接返回该字符串对应的对象。因为hash表查找比我的编辑距离（Edit Distance）计算相似距离的方法快（编辑距离是循环hash表，表中每个单词都做比对），所以我们首先使用hash表的find方法查找输入的单词是不是正确的单词，如果不是，我们再使用动态规划优化后的编辑距离计算相似距离的方法找出三个最为相似的单词输出。

程序代码：

动态规划求编辑距离的核心代码：

package tst;

    /**
    *
    *@ClassName EditDistance.java 
    *@author Leno E-mail:[email protected]
    *@date 2017年12月7日下午1:28:27
    *@Description 动态规划思想求编辑距离，从前往后算
    */

public class EditDistance {
    public int min(int a,int b,int c){
        int tmp = areturn tmppublic int edit_distance(String a,String b){
        int lena = a.length();
        int lenb = b.length();
        int d[][] = new int[lena+1][lenb+1];
        int i = 0 , j = 0;
        for(i=0;i<=lena;i++){
            d[i][0] = i;
        }
        for(j=0;j<=lenb;j++){
            d[0][j] = j;
        }
        for(i=1;i<=lena;i++){
            for(j=1;j<=lenb;j++){
                if(a.charAt(i-1) == b.charAt(j-1)){
                    d[i][j] = d[i-1][j-1];
                }else{
                    d[i][j] = min(d[i-1][j]+1,d[i][j-1]+1,d[i-1][j-1]+1);
                }
            }
        }
        return d[lena][lenb]; 
    }
}

测试例和运行结果：

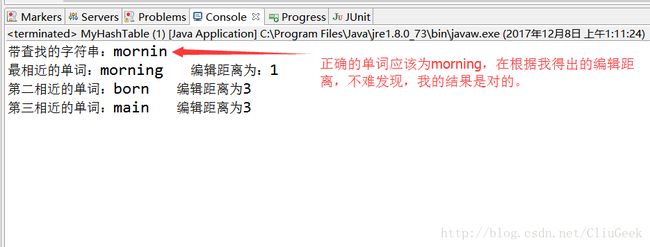
这次的测试例给的比较多，我随便输入了几个单词进行了相应的测试，结果如下：

以上是本次作业的核心实现部分，如果有不正确的地方，还希望大家不吝指正。