Python金融系列第六篇:现代投资组合理论
作者:chen_h
微信号 & QQ:862251340
微信公众号:coderpai
第一篇:计算股票回报率,均值和方差
第二篇:简单线性回归
第三篇:随机变量和分布
第四篇:置信区间和假设检验
第五篇:多元线性回归和残差分析
第六篇:现代投资组合理论
第七篇:市场风险
第八篇:Fama-French 多因子模型
介绍
现代投资组合理论(MPT)表明投资者应如何在各种投资中分配财务,以最大限度地降低风险并最大化回报。本章在数学公式上有点多,所以得慢慢看。
风险厌恶
在投资组合理论中,资产的风险通常通过其收益的方差(或者标准差)来衡量。规避风险的投资者不希望他们的财富大幅波动。
可以通过一个简单的例子来说明风险规避。比如有以下两种资产,你更加喜欢哪一种资产呢?
- 资产 A 获得 200 美元或者 0 美元,每个选择概率为 50%;
- 资产 B 获得 400 美元或者 -200 美元,每个选择概率为 50%;
资产 A 和资产 B 的预期回报为:
E ( A ) = 0.5 ∗ 200 + 0.5 ∗ 0 = 100 E(A) = 0.5*200+0.5*0=100 E(A)=0.5∗200+0.5∗0=100
E ( B ) = 0.5 ∗ 400 + 0.5 ∗ ( − 200 ) = 100 E(B) = 0.5*400+0.5*(-200)=100 E(B)=0.5∗400+0.5∗(−200)=100
他们的回报标准差为:
σ A = 0.5 ( 200 − 100 ) 2 + 0.5 ( 0 − 100 ) 2 = 100 \sigma_{A} = \sqrt{0.5(200-100)^{2}+0.5(0-100)^{2}} = 100 σA=0.5(200−100)2+0.5(0−100)2=100
σ A = 0.5 ( 400 − 100 ) 2 + 0.5 ( − 200 − 100 ) 2 = 300 \sigma_{A} = \sqrt{0.5(400-100)^{2}+0.5(-200-100)^{2}} = 300 σA=0.5(400−100)2+0.5(−200−100)2=300
如果你是风险追求者,你可以选择资产 B,因为你可以获得更高的回报。MPT 假设投资者更喜欢资产 A,因为两种资产的预期收益是一样的,但是资产 A 的风险较小。
投资组合
假设我们将我们财富的一部分 w 1 , w 2 , ⋯ , w n w_1, w_2, \cdots, w_n w1,w2,⋯,wn 投资于 n 个风险资产(标记为 1 到 n),其余部分投资于无风险资产,例如银行账户中的现金。
显然, w 0 + w 1 + w 2 + ⋯ + w n = 1 w_0 + w_1 + w_2 + \cdots + w_n = 1 w0+w1+w2+⋯+wn=1 ,因为我们的财富包含所有这些资产。假设, R 0 , R 1 , R 2 , ⋯ , R N R_0, R_1, R_2, \cdots, R_N R0,R1,R2,⋯,RN 为各自的资产收益率,然后我们的投资组合收益率为:
R p = w 0 R 0 + w 1 R 1 + ⋯ + w n R n R_p = w_0R_0+w_1R_1+ \cdots +w_nR_n Rp=w0R0+w1R1+⋯+wnRn
或者,我们可以消除 w 0 w_0 w0 得到:
R p − R 0 = w 1 ( R 1 − R 0 ) + ⋯ + w n ( R n − R 0 ) R_p - R_0 = w_1(R_1-R_0)+ \cdots + w_n(R_n-R_0) Rp−R0=w1(R1−R0)+⋯+wn(Rn−R0)
那么,我们的预期投资回报是:
E ( R p ) = w 0 R 0 + w 1 E ( R 1 ) + ⋯ + w n E ( R n ) E(R_p) = w_0R_0+w_1E(R_1)+\cdots+w_nE(R_n) E(Rp)=w0R0+w1E(R1)+⋯+wnE(Rn)
注意: E ( R 0 ) = R 0 E(R_0) = R_0 E(R0)=R0 ,因为根据定义,无风险回报是固定的。
相关性
在计算投资组合风险之前,我们首先需要了解协方差和相关性。我们测量两个随机变量之间的线性关系。
两个随机变量 X 和 Y 的协方差定义为:
C o v ( X , Y ) = E [ ( X − E ( X ) ) ( Y − E ( Y ) ) ] Cov(X, Y) = E[(X-E(X))(Y-E(Y))] Cov(X,Y)=E[(X−E(X))(Y−E(Y))]
X 和 Y 的相关性(始终在 -1 和 1 之间)是标准化之后的协方差:
C o r r ( X , Y ) = C o v ( X − E ( X ) σ X , Y − E ( Y ) σ Y ) = C o v ( X , Y ) σ X σ Y Corr(X, Y) = Cov(\frac{X-E(X)}{\sigma_{X}}, \frac{Y-E(Y)}{\sigma_{Y}})=\frac{Cov(X,Y)}{\sigma_{X}\sigma_{Y}} Corr(X,Y)=Cov(σXX−E(X),σYY−E(Y))=σXσYCov(X,Y)
风险
现在我们已经准备好计算投资组合风险,通过投资组合回报的方差来衡量:
V a r ( R p ) = V a r ( w 0 R 0 + w 1 R 1 + ⋯ + w n R n ) Var(R_{p}) = Var(w_0R_0+w_1R_1+ \cdots + w_nR_n) Var(Rp)=Var(w0R0+w1R1+⋯+wnRn)
回想一下,如果 c 是已知常数,则 V a r ( x + c ) = V a r ( x ) Var(x+c) = Var(x) Var(x+c)=Var(x) ,因此可以省略涉及无风险返回的项 w 0 R 0 w_0R_0 w0R0 。即:
V a r ( R p ) = V a r ( ∑ k = 1 n w k R k ) = E [ ( ∑ k = 1 n w k R k − E ( ∑ k = 1 n w k R k ) ) 2 ] = E [ ( ∑ k = 1 n w k ( R k − E ( R k ) ) ) 2 ] Var(R_{p}) = Var(\sum_{k=1}^{n}w_{k}R_{k})=E[(\sum_{k=1}^{n}w_{k}R_{k}-E(\sum_{k=1}^{n}w_{k}R_{k}))^{2}]=E[(\sum_{k=1}^{n}w_{k}(R_{k}-E(R_{k})))^{2}] Var(Rp)=Var(∑k=1nwkRk)=E[(∑k=1nwkRk−E(∑k=1nwkRk))2]=E[(∑k=1nwk(Rk−E(Rk)))2]
所以,我们有 n 个项的平方和。那么,我们如何扩展它呢?
( ∑ k = 1 n u k ) 2 = ( μ 1 + ⋯ + μ n ) ( μ 1 + ⋯ + μ n ) (\sum_{k=1}^{n}u_{k})^{2}=(\mu_{1}+\cdots+\mu_{n})(\mu_{1}+\cdots+\mu_{n}) (∑k=1nuk)2=(μ1+⋯+μn)(μ1+⋯+μn)
如果我们对等号右侧的式子进行简化,那么我们可以得到如下式子:
( ∑ k = 1 n u k ) 2 = ∑ i = 1 n ∑ j = 1 n μ i μ j (\sum_{k=1}^{n}u_{k})^{2}=\sum_{i=1}^{n}\sum_{j=1}^{n}\mu_{i}\mu_{j} (∑k=1nuk)2=∑i=1n∑j=1nμiμj
因此,
V a r ( R p ) = E [ ∑ i = 1 n ∑ j = 1 n w i w j ( R i − E ( R i ) ) ( R j − E ( R j ) ) ] = ∑ i = 1 n ∑ j = 1 n w i w j C o v ( R i , R j ) Var(R_{p}) = E[\sum_{i=1}^{n} \sum_{j=1}^{n}w_{i}w_{j}(R_{i} - E(R_{i}))(R_{j} - E(R_{j}))] = \sum_{i=1}^{n} \sum_{j=1}^{n} w_{i} w_{j} Cov(R_{i}, R_{j}) Var(Rp)=E[∑i=1n∑j=1nwiwj(Ri−E(Ri))(Rj−E(Rj))]=∑i=1n∑j=1nwiwjCov(Ri,Rj)
我们可以看到,最后一步来自协方差的定义。这里唯一剩下的就是以矩阵表示法表达投资组合风险:
V a r ( R p ) = w T ∑ w Var(R_{p}) = w^{T}\sum w Var(Rp)=wT∑w
其中,
w = ( w 1 ⋮ w n ) w=\begin{pmatrix} w_{1}\\ \vdots \\ w_{n} \end{pmatrix} w=⎝⎜⎛w1⋮wn⎠⎟⎞
∑ = [ C o v ( R 1 , R 1 ) C o v ( R 1 , R 2 ) ⋯ C o v ( R 1 , R n ) C o v ( R 2 , R 1 ) C o v ( R 2 , R 2 ) ⋯ C o v ( R 2 , R n ) ⋮ ⋮ ⋱ ⋮ C o v ( R n , R 1 ) C o v ( R n , R 2 ) ⋯ C o v ( R n , R n ) ] \sum=\begin{bmatrix} Cov(R_1, R_1) & Cov(R_1, R_2) & \cdots &Cov(R_1, R_n) \\ Cov(R_2, R_1) & Cov(R_2, R_2) & \cdots &Cov(R_2, R_n) \\ \vdots & \vdots & \ddots & \vdots \\ Cov(R_n, R_1) & Cov(R_n, R_2) & \cdots & Cov(R_n, R_n) \end{bmatrix} ∑=⎣⎢⎢⎢⎡Cov(R1,R1)Cov(R2,R1)⋮Cov(Rn,R1)Cov(R1,R2)Cov(R2,R2)⋮Cov(Rn,R2)⋯⋯⋱⋯Cov(R1,Rn)Cov(R2,Rn)⋮Cov(Rn,Rn)⎦⎥⎥⎥⎤
直观
我们如何理解投资组合风险呢?考虑一个带有无风险资产的简单案例,只有 n = 2 个风险资产。
V a r ( R p ) = w A 2 V a r ( R A ) + w B 2 V a r ( R B ) + 2 w A w B C o v ( R A , R B ) Var(R_{p}) = w_{A}^{2}Var(R_{A}) + w_{B}^{2}Var(R_{B}) + 2w_{A}w_{B}Cov(R_{A}, R_{B}) Var(Rp)=wA2Var(RA)+wB2Var(RB)+2wAwBCov(RA,RB)
通过选择两个负相关的资产可以降低投资组合风险。这就是多样化投资的好处。
均值-方差分析
我们现在试图找到一个投资组合 w = ( w 1 , ⋯ , w n ) w = (w_{1}, \cdots, w_{n}) w=(w1,⋯,wn) ,它可以最大限度的降低风险并获得最大化回报。
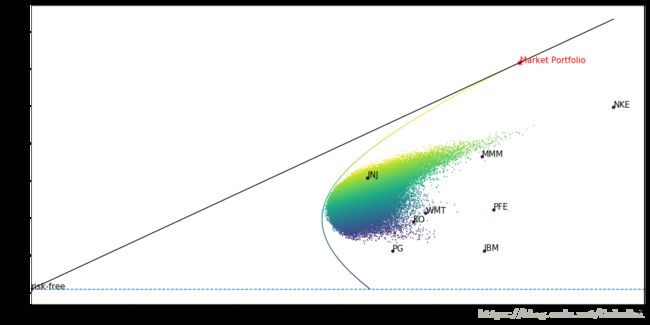
下表中横轴表示风险(收益标准差),纵轴表示预期收益,10 个黑点表示个股,而每一个绿色/蓝色表示股票组合:
请注意,所有点(即股票和投资组合)都被双曲线包围,称为有效前沿。如果我们只考虑风险股票的投资组合,那么有效边界的所有投资组合都会在给定的风险水平下获得最大的预期回报。我们可以通过包含无风险资产来获得更高的回报吗?答案是肯定的。
资本市场线
图表上的黑线代表资本市场线(CML)。它与有效边界相切,并在无风险回报时切割垂直轴。相切点代表所谓的市场投资组合。CML 上的没一点代表一个投资组合,包括市场投资组合和一定比例的无风险资产。为什么呢?假设 CML 投资组合的一部分 w 是市场投资组合,其余部分(1-w)是无风险资产。然后它的预期回报是:
E ( R p ) = w E ( R m a r k d e t ) + ( 1 − w ) R 0 E(R_{p}) = wE(R_{markdet}) + (1-w)R_{0} E(Rp)=wE(Rmarkdet)+(1−w)R0
由于只有 n = 1 风险资产,因此 CML 投资组合收益的方差为:
Var ( R P ) = w 2 Var R market \text{Var}(R_P) = w^2 \text{Var}{R_{\text{market}}} Var(RP)=w2VarRmarket
从平方根来看,我们推断出 CML 投资组合的风险与市场投资组合的权重成正比:
σ p = w σ m a r k e t \sigma_{p} = w \sigma_{market} σp=wσmarket
该等式可用于消除预期收益计算中的 w:
E ( R p ) = R 0 + E ( R m a r k e t ) − R 0 σ m a r k e t σ p E(R_{p}) = R_{0} + \frac{E(R_{market}) - R_{0}}{\sigma_{market}} \sigma_{p} E(Rp)=R0+σmarketE(Rmarket)−R0σp
这证明当 E ( R p ) E(R_{p}) E(Rp) 和 σ p \sigma_{p} σp 绘制在图上时,我们就能得到一条直线:CML。
组合选择
为什么 CML 如此重要呢?对于任何给定的风险水平,CML 投资组合的回报高于有效边界的回报,因此投资者应根据其风险承受能力选择任何一个。规避风险的投资者可能会使无风险资产在其投资组合中占据更大比重。寻求风险的投资者可以借入资金(即出售无风险资产),将其 100% 的财富投资于市场投资组合。无论风险承受能力如何,所有投资者都应在市场投资组合中持有相同比例的相同股票。换句话说,他们不应该根据它们的风险承受能力来挑选股票。
多样化
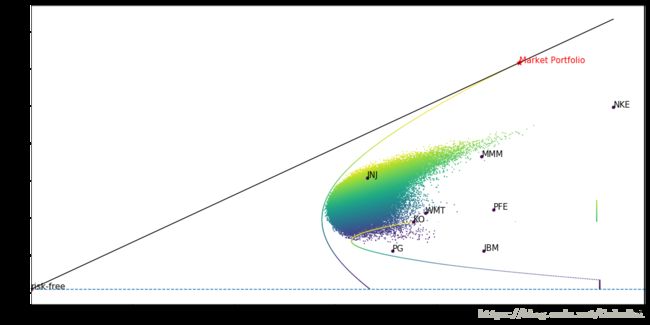
如果我们只有 3 只股票(IBM,GE和PFE)而不是 10 只股票,那么有效边界和 CML 会发生什么呢?
由于我们可以选择的股票较少,因此对于任何风险水平,我们的最大预期回报率都会降低并不令人惊讶。这说明为什么多元化经常被认为是投资中的免费午餐。