数学建模（四）数据统计描述与分析（方差分析，回归分析）

1.数据统计描述与分析

标题像一本书的名字，感觉好厉害有没有，没有，跟数理统计差不多。方法要用matlab的statistic工具箱。包括均值啊方差啊直方图啊概率分布，这里介绍一下假设检验（就因为我不太会）。

1.1 σ^2 已知，关于 μ 的检验（ Z 检验）

在 Matlab 中 Z 检验法由函数 ztest 来实现，命令为[h,p,ci]=ztest(x,mu,sigma,alpha,tail)，其中输入参数 x 是样本，mu 是 H0 中的 μ0 ，sigma 是总体标准差σ ，alpha 是显著性水平α （alpha 缺省时设定为 0.05），tail 是对备选假设 H1 的选择： H1 为 μ ≠ μ0 时用 tail=0（可缺省）； H1 为 μ > μ0 时用 tail=1； H1 为 μ < μ0 时用 tail=-1。输出参数 h=0 表示接受 H0 ，h=1 表示拒绝 H0 ，p 表示在假设 H0 下样本均值出现的概率，p越小 H0 越值得怀疑，ci 是 μ0 的置信区间。
例：某车间用一台包装机包装糖果。包得的袋装糖重是一个随机变量，它服从正
态分布。当机器正常时，其均值为 0.5 公斤，标准差为 0.015 公斤。某日开工后为检验包装机是否正常，随机地抽取它所包装的糖 9 袋，称得净重为（公斤）：
0.497 0.506 0.518 0.524 0.498 0.511 0.520 0.515 0.512，问机器是否正常？
解 总体σ 已知， x ~ N(μ,0.0152 ) ， μ 未知。 于是提出假设 H0 : μ = μ0 = 0.5和
: 0.5，H1：μ ≠ 0.5。

x=[0.497 0.506 0.518 0.524 0.498...
0.511 0.520 0.515 0.512];
[h,p,ci]=ztest(x,0.5,0.015)

h =

     1


p =

    0.0248


ci =

    0.5014    0.5210

h=1,拒绝原假设。

1.2 σ2 未知，关于 μ 的检验（ t 检验）

在 Matlab 中t 检验法由函数 ttest 来实现，命令为
[h,p,ci]=ttest(x,mu,alpha,tail).例：
某种电子元件的寿命 x (以小时计)服从正态分布, μ,σ 2 均未知.现得 16 只元件的寿命如下:
159 280 101 212 224 379 179 264
222 362 168 250 149 260 485 170
问是否有理由认为元件的平均寿命大于 225(小时)?
解：按题意需检验，H0 : μ ≤ μ0 = 225, H1 : μ > 225，取α = 0.05 。

x=[159 280 101 212 224 379 179 264 ...
222 362 168 250 149 260 485 170];
[h,p,ci]=ttest(x,225,0.05,1)

h =

     0


p =

    0.2570


ci =

  198.2321       Inf

求得 h=0，p=0.2570，说明在显著水平为 0.05 的情况下，不能拒绝原假设，认为
元件的平均寿命不大于 225 小时。

1.3 两个正态总体均值差的检验（ t 检验）

还可以用 t 检验法检验具有相同方差的 2 个正态总体均值差的假设。在 Matlab 中
由函数 ttest2 实现，命令为：
[h,p,ci]=ttest2(x,y,alpha,tail)
与上面的 ttest 相比，不同处只在于输入的是两个样本 x,y（长度不一定相同），
而不是一个样本和它的总体均值；tail 的用法与 ttest 相似，可参看帮助系统。
例：在平炉上进行一项试验以确定改变操作方法的建议是否会增加钢的得率,试
验是在同一平炉上进行的。每炼一炉钢时除操作方法外,其它条件都可能做到相同。先用标准方法炼一炉,然后用建议的新方法炼一炉,以后交换进行,各炼了 10 炉,其得率分别为
1°标准方法 78.1 72.4 76.2 74.3 77.4 78.4 76.0 75.6 76.7 77.3
2°新方法 79.1 81.0 77.3 79.1 80.0 79.1 79.1 77.3 80.2 82.1
设这两个样本相互独立且分别来自正态总体 N(μ1,σ 2 ) 和 N(μ2,σ2 ) , μ1,μ2,σ2 均未知，问建议的新方法能否提高得率?(取α = 0.05 。)
解 （i）需要检验假设
H0 μ1 − μ2 ≥ 0， H1 : μ1 − μ2 < 0 .

x=[78.1 72.4 76.2 74.3 77.4 78.4 76.0 75.6 76.7 77.3];
y=[79.1 81.0 77.3 79.1 80.0 79.1 79.1 77.3 80.2 82.1];
[h,p,ci]=ttest2(x,y,0.05,-1)

h =

     1


p =

   2.2126e-04


ci =

      -Inf   -1.9000

求得 h=1,p=2.2126×10-4。表明在α = 0.05 的显著水平下，可以拒绝原假设，即认
为建议的新操作方法较原方法优。
注： ttest2 既可以做方差相等的，又可以做方差不相等的假设检验，使用格式为
h = ttest2(x,y,alpha,tail, ‘unequal’)。

2.方差分析

为了使生产过程稳定，达到优质、高产，需要对影响产品质量的因素进行分析， 找出有显著影响的那些因素， 除了从机理方面进行研究外， 常常要作许多试验，对结果作分析、比较，寻求规律。用数理统计分析试验结果、鉴别各因素对结果影响程度的方法称为方差分析（ Analysis Of Variance），记作 ANOVA。
方差分析一般用的显著性水平是：取α = 0.01，拒绝 H 0 ，称因素 A 的影响（或 A
各水平的差异）非常显著；取α = 0.01，不拒绝 H0 ，但取α = 0.05 ，拒绝 H 0 ，称因素 A 的影响显著；取α = 0.05 ，不拒绝 H0 ，称因素 A 无显著影响。

2.1 单因素方差分析

只考虑一个因素 A 对所关心的指标的影响， A 取几个水平，在每个水平上作若干
个试验，试验过程中除 A 外其它影响指标的因素都保持不变（只有随机因素存在），我们的任务是从试验结果推断，因素 A 对指标有无显著影响，即当 A 取不同水平时指标有无显著差别。
A 取某个水平下的指标视为随机变量，判断 A 取不同水平时指标有无显著差别，
相当于检验若干总体的均值是否相等。
若各组数据个数相等，称为均衡数据。若各组数据个数不等，称非均衡数据。

2.1.1 均衡数据

p=anoval(x)，返回值 p 是一个概率，当 p > α 时接受 H 0 ， x 为 m× r 的数据矩阵， x 的每一列是一个水平的数据（这里各个水平上的样本容量 ni = m ）。另外，还输出一个方差表和一个Box 图。

x=[256 254 250 248 236
242 330 277 280 252
280 290 230 305 220
298 295 302 289 252];
p=anova1(x)

p =

    0.1109

求得 p = 0.1109 >α = 0.05 ，故接受 H0 ，即 5 列数据没有显著差异。方差表对应于上面的单因素方差分析表的1 ~ 4 列， F = 2.262 是 F(4,15) 分布的1− p 分位数，box图反映了各组数据的特征。

2.1.2 非均衡数据

p=anova1(x,group)。x 为向量，从第 1 组到第 r 组数据依次排列；group 为与 x 同长度的向量，标志 x 中数据的组别（在与 x 第i 组数据相对应的位置处输入整数i(i = 1,2,L,r) ）。

x=[1620 1580 1460 1500
1670 1600 1540 1550
1700 1640 1620 1610
1750 1720 1680 1800];
x=[x(1:4),x(16),x(5:8),x(9:11),x(12:15)];
g=[ones(1,5),2*ones(1,4),3*ones(1,3),4*ones(1,4)];
p=anova1(x,g)
p =

    0.0331

求得 0.01

2.2 双因素方差分析

如果要考虑两个因素 A, B 对指标的影响， A, B 各划分几个水平，对每一个水平组
合作若干次试验，对所得数据进行方差分析，检验两因素是否分别对指标有显著影响，或者还要进一步检验两因素是否对指标有显著的交互影响。
p=anova2(x,reps)。其中 x 不同列的数据表示单一因素的变化情况， 不同行中的数据表示另一因素的变化情况。如果每种行—列对（“单元”）有不止一个的观测值，则用参数 reps 来表明每个“单元”多个观测值的不同标号，即 reps 给出重复试验的次数t 。
例：一种火箭使用了四种燃料、三种推进器，进行射程试验，对于每种燃料与每
种推进器的组合作一次试验，得到试验数据如表 8。问各种燃料之间及各种推进器之间有无显著差异？

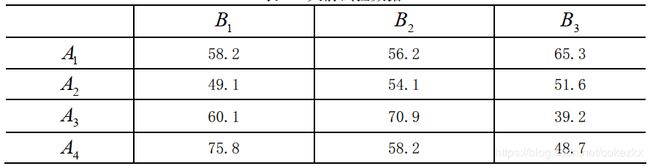
解 记燃料为因素 A ， 它有 4 个水平， 水平效应为αi,i =1,2,3,4 。 推进器为因素 B ，它有 3 个水平，水平效应为 β j, j =1,2,3。我们在显著性水平α = 0.05 下检验
H1：α1 = α 2 = α3 = α 4 =0，H2：β1 = β2 = β3 = 0。

x=[58.2 56.2 65.3
49.1 54.1 51.6
60.1 70.9 39.2
75.8 58.2 48.7];
[p,t,st]=anova2(x)

p =

    0.4491    0.7387


t =

  5×6 cell 数组

  1 至 4 列

    'Source'     'SS'            'df'    'MS'      
    'Columns'    [  223.8467]    [ 2]    [111.9233]
    'Rows'       [  157.5900]    [ 3]    [ 52.5300]
    'Error'      [  731.9800]    [ 6]    [121.9967]
    'Total'      [1.1134e+03]    [11]            []

  5 至 6 列

    'F'         'Prob>F'
    [0.9174]    [0.4491]
    [0.4306]    [0.7387]
          []          []
          []          []


st = 

  包含以下字段的 struct:

      source: 'anova2'
     sigmasq: 121.9967
    colmeans: [60.8000 59.8500 51.2000]
        coln: 4
    rowmeans: [59.9000 51.6000 56.7333 60.9000]
        rown: 3
       inter: 0
        pval: NaN
          df: 6

根据p值，接受H0，表明各种燃料和各种推进器之间的差异对于火箭射程无显著影响。

2.3 正交试验设计与方差分析

前面介绍了一个或两个因素的试验，由于因素较少，我们可以对不同因素的所有可
能的水平组合做试验，这叫做全面试验。当因素较多时，虽然理论上仍可采用前面的方法进行全面试验后再做相应的方差分析，但是在实际中有时会遇到试验次数太多的问题。因此在实际应用中，对于多因素做全面试验是不现实的。于是我们考虑是否可以选择其中一部分组合进行试验，这就要用到试验设计方法选择合理的试验方案，使得试验次数不多，但也能得到比较满意的结果。
例:为提高某种化学产品的转化率（％），考虑三个有关因素：反应温度A（℃），反应时间 B（min）和使用催化剂的含量C（％）。各因素选取三个水平，如下表所示。

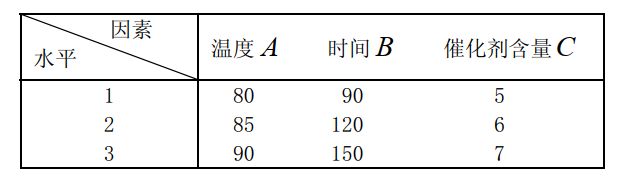
原理用到正交表，这里不详细讲了，参见代码：

y=[31 54 38 53 49 42 57 62 64];
g1=[1 2 3 1 2 3 1 2 3];
g2=[1 1 1 2 2 2 3 3 3];
g3=[2 1 3 1 3 2 3 2 1];
[p,t,st]=anovan(y,{g1,g2,g3})

y是对应排列所得转化率（其实这有点不清楚，这个转化率是题目已知的吗，这默认是已知的）。求得概率 p= 0.1364 0.0283 0.0714，可见因素 B、 C 的各水平对指标值的影响有显著差异（显著性水平取 0.1），而因素 A 的各水平对指标值的影响无显著差异。

3.回归分析

前面说过拟合和回归的区别，再说一遍敲黑板。曲线拟合问题的特点是，根据得到的若干有关变量的一组数据，寻找因变量与（一个或几个）自变量之间的一个函数，使这个函数对那组数据拟合得最好。通常，函数的形式可以由经验、先验知识或对数据的直观观察决定，要作的工作是由数据用最小二乘法计算函数中的待定系数。从计算的角度看，问题似乎已经完全解决了，还有进一步研究的必要吗?
从数理统计的观点看，这里涉及的都是随机变量，我们根据一个样本计算出的那些
系数，只是它们的一个（点）估计，应该对它们作区间估计或假设检验，如果置信区间太大，甚至包含了零点，那么系数的估计值是没有多大意义的。另外也可以用方差分析方法对模型的误差进行分析，对拟合的优劣给出评价。简单地说，回归分析就是对拟合问题作的统计分析。
可以用SPSS作，过程略。