队列的基本操作(顺序队列、循环队列、链式队列)
队列也是一种线性表,是一种先进先出的线性结构。队列只允许在表的一端进行插入(入队)、删除(出队)操作。允许插入的一端称为队尾,允许删除的一端称为队头。
队列的基本操作包括:
- 初始化队列:InitQueue(Q)
操作前提:Q为未初始化的队列。
操作结果:将Q初始化为一个空队列。- 判断队列是否为空:IsEmpty(Q)
操作前提:队列Q已经存在。
操作结果:若队列为空则返回1,否则返回0。- 判断队列是否已满:IsFull(Q)
操作前提:队列Q已经存在。
操作结果:若队列为满则返回1,否则返回0。- 入队操作:EnterQueue(Q,data)
操作前提:队列Q已经存在。
操作结果:在队列Q的队尾插入data。- 出队操作:DeleteQueue(Q,&data)
操作前提:队列Q已经存在且非空。
操作结果:将队列Q的队头元素出队,并使用data带回出队元素的值。- 取队首元素:GetHead(Q,&data)
操作前提:队列Q已经存在且非空。
操作结果:若队列为空则返回1,否则返回0。- 清空队列:ClearQueue(&Q)
操作前提:队列Q已经存在。
操作结果:将Q置为空队列。
队列有两种存储形式:顺序存储和链式存储。采用顺序队列存储的队列称为顺序队列,采用链式存储的队列称为链式队列。顺序队列采用数组存储队列中的元素,使用两个指针尾指针(rear)和头指针(front)分别指向队列的队头和队尾。使用顺序队列由于在操作时会出现“假溢出现象”,所以可以使用顺序循环队列合理的使用队列空间。链式队列使用链表来实现,链表中的数据域用来存放队列中的元素,指针域用来存放队列中下一个元素的地址,同时使用队头指针指向队列的第一个元素和最后一个元素。
顺序队列的基本操作
/*----------------------------------------------------------------
设立一个队首指针front ,一个队尾指针rear ,分别指向队首和队尾元素。
◆ 初始化:front=rear=0。
◆ 队列为空:front=rear。
◆ 队满:rear=MaxSize。
◆ 入队:将新元素插入rear所指的位置,然后rear加1。
◆ 出队:删去front所指的元素,然后加1并返回被删元素。
◆ 取队首元素:返回fornt指向的元素值
-----------------------------------------------------------------*/
#include rear)
{
printf("%-3d", SQ->Queue[i]);
i++;
}
printf("\n");
}
int main()
{
SeqQueue SQ;
DataType data;
//初始化队列
InitQueue(&SQ);
//入队
EnterQueue(&SQ, 1);
EnterQueue(&SQ, 2);
EnterQueue(&SQ, 3);
EnterQueue(&SQ, 4);
EnterQueue(&SQ, 5);
EnterQueue(&SQ, 6);
EnterQueue(&SQ, 8);
EnterQueue(&SQ, 10);
EnterQueue(&SQ, 12);
EnterQueue(&SQ, 15);
EnterQueue(&SQ, 16);
//打印队列中的元素
printf("队列中的元素为:");
PrintQueue(&SQ);
printf("\n");
//出队
DeleteQueue(&SQ, &data);
printf("出队元素为:%d\n", data);
printf("\n");
DeleteQueue(&SQ, &data);
printf("出队元素为:%d\n", data);
printf("\n");
printf("队列中的元素为:");
PrintQueue(&SQ);
printf("\n");
//获取队首元素
data = GetHead(&SQ, &data);
printf("队首元素为:%d\n", data);
printf("#元素16入队#\n");
//元素16入队
EnterQueue(&SQ, 16);
printf("队列中的元素为:");
PrintQueue(&SQ);
printf("\n");
system("pause");
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
测试结果
队列已满
队列中的元素为:1 2 3 4 5 6 8 10 12 15
出队元素为:1
出队元素为:2
队列中的元素为:3 4 5 6 8 10 12 15
队首元素为:3
/#元素16入队#
队列已满
队列中的元素为:3 4 5 6 8 10 12 15
请按任意键继续…
在上面的代码里,我们定义的队列的最大容量为:10,依此调用入队函数EnterQueue,将1,2,3,4,5,6,8,10,12,15,16总共11个元素依此入队,我们看到运行结果最先输出队列已满,这是因为16入队时,队列以达到最大容量,所以,输出提示信息“队列已满”,打印队列中的元素结果入第二行1,2,3,4,5,6,8,10,12,15。然后依此测试了出队,取队首元素等函数,仔细观察,可以发现在测试出队时,依此出队两次,此时打印队列中的元素值为3,4,5,6,8,10,12,15总共8个元素值。我们定义的队列的最大容量为10,出队两次后队列中的元素个数为8,则队列中还有两个空间,但再次执行入队操作EnterQueue(&SQ, 16); 发现并没有将16成功入队,而是输出提示“队列已满”,再次打印队列中的元素,发现队列中依然只有8个元素。这时怎么回事儿呢?其实这就是文章前边提到的顺序队列的“假溢出现象”。
所谓假溢出现象,即队头由于出队操作,还有剩余空间,但队尾指针已达到数组的末尾,如果继续插入元素,队尾指针就会越出数组的上界,而造成“溢出”,这种溢出不是因为存储空间不够而产生的溢出,而是经过多次插入删除操作引起的,像这中有存储空间而不能插入元素的操作称为“假溢出“。可以通过下面的图爿理解假溢出。
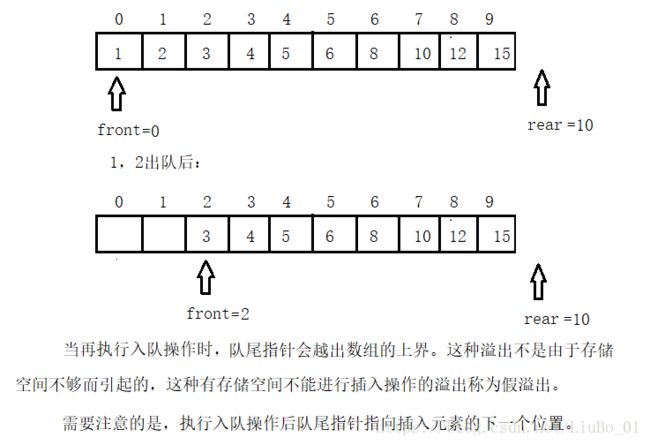
为了充分利用存储空间,消除这种”假溢出”,可以采用的方法是:将为队列分配的空间看成为一个首尾相接的圆环,并称这种队列为循环队列。
在循环队列中进行出队、入队操作时,队首、队尾指针仍要加1,指针移动。只不过当队头指针front 指向向量上界(MaxSize-1)时,其加1操作的结果是指向向量的下界0。
这种循环意义下的加1操作可以描述为:
if (i+1==MaxSize) i=0;
else i++ ;
- 1
- 2
其中: i代表队首指针front(出队时);或队尾指针rear(入队时),用模运算可简化为:i=(i+1)%MaxSize ;显然,循环队列所分配的空间可以被充分利用,除非向量空间真的被队列元素全部占用,否则不会上溢。
循环队列在队空和队满时,都是队头指针和队尾指针指向同一个位置,即:front==rear 为了区分这两种情况,可以少用一个存储空间,队空的判断条件不变,以队尾指针rear加1等于队头指针为队列的判满条件。即:front = rear 表示队空,(rear + 1) % MaxSize == fornt 表示队满。
循环队列的基本操作
/*----------------------------------------------------------------
设立一个队首指针front ,一个队尾指针rear ,分别指向队首和队尾元素。
◆ 初始化:front=rear=0。
◆ 队列为空:front=rear。
◆ 队满:(rear + 1) % MaxSize == fornt
◆ 入队:将新元素插入rear所指的位置,然后rear加1。
◆ 出队:删去front所指的元素,然后加1并返回被删元素。
◆ 取队首元素:返回fornt指向的元素值
-----------------------------------------------------------------*/
#includerear + MaxSize; i++)
{
printf("%-3d", SCQ->Queue[i]);
}
}
printf("\n");
}
int main()
{
SeqCirQueue SCQ;
DataType data;
//初始化队列
InitSeqCirQueue(&SCQ);
//入队
EnterSeqCirQueue(&SCQ, 1);
EnterSeqCirQueue(&SCQ, 2);
EnterSeqCirQueue(&SCQ, 4);
EnterSeqCirQueue(&SCQ, 6);
EnterSeqCirQueue(&SCQ, 8);
EnterSeqCirQueue(&SCQ, 9);
EnterSeqCirQueue(&SCQ, 10);
EnterSeqCirQueue(&SCQ, 12);
EnterSeqCirQueue(&SCQ, 13);
printf("队列中元素为:\n");
//打印队列中元素
PrintSeqCirQueue(&SCQ);
EnterSeqCirQueue(&SCQ, 15);
//出队
DeleteSeqCirQueue(&SCQ, &data);
printf("出队元素为:%d\n", data);
printf("\n");
printf("队列中元素为:\n");
PrintSeqCirQueue(&SCQ);
printf("15入队:\n");
EnterSeqCirQueue(&SCQ, 15);
printf("队列中元素为:\n");
PrintSeqCirQueue(&SCQ);
system("pause");
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
测试结果
队列中元素为:
1 2 4 6 8 9 10 12 13
队列已满,不能入队!
出队元素为:1
队列中元素为:
2 4 6 8 9 10 12 13
15入队:
队列中元素为:
2 4 6 8 9 10 12 13 15
请按任意键继续…
为了区分队空和队满的条件,少用了一个存储空间,所以队列的实际存储空间为9,当入队9个元素时,再入队显示队列已满,当出队一个元素后,队列中剩余一个存储空间,我们执行入队操作,成功将元素15入队,从而消除了”假溢出现象“。
队列的链式存储结构简称为链式队列,它是限制仅在表头进行删除操作和表尾进行插入操作的单链表。链队的操作实际上是单链表的操作,只不过是出队在表头进行,入队在表尾进行。入队、出队时分别修改不同的指针。链式队列的出队和入队的操作可参考下图:
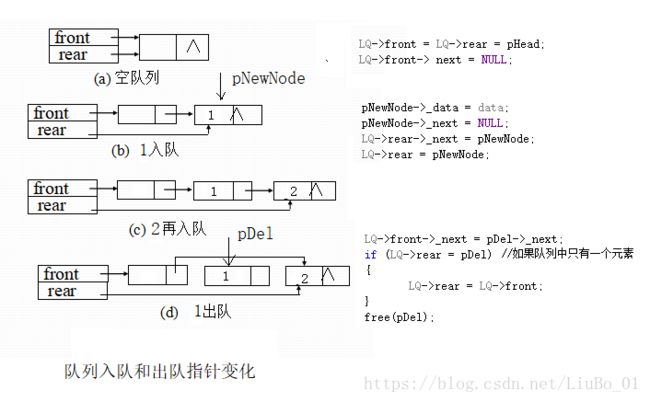
**链式队列的基本操作
#include <stdio.h>
#include <Windows.h>
#include <stdlib.h>
#include <assert.h>
typedef int DataType;
typedef struct Node
{
DataType _data;
struct Node* _next;
}LinkQueueNode;
typedef struct
{
LinkQueueNode* front;
LinkQueueNode* rear;
}LinkQueue;
//初始化队列
void InitLinkQueue(LinkQueue* LQ)
{
//创建一个头结点
LinkQueueNode* pHead = (LinkQueueNode*)malloc(sizeof(LinkQueueNode));
assert(pHead);
LQ->front = LQ->rear = pHead; //队头和队尾指向头结点
LQ->front->_next = NULL;
}
//判断队列是否为空
int IsEmpty(LinkQueue* LQ)
{
if (LQ->front->_next == NULL)
{
return 1;
}
return 0;
}
//入队操作
void EnterLinkQueue(LinkQueue* LQ, DataType data)
{
//创建一个新结点
LinkQueueNode* pNewNode = (LinkQueueNode*)malloc(sizeof(LinkQueueNode));
assert(pNewNode);
pNewNode->_data = data; //将数据元素赋值给结点的数据域
pNewNode->_next = NULL; //将结点的指针域置空
LQ->rear->_next = pNewNode; //将原来队列的队尾指针指向新结点
LQ->rear = pNewNode; //将队尾指针指向新结点
}
//出队操作
void DeleteLinkQueue(LinkQueue* LQ,DataType* data)
{
if (IsEmpty(LQ))
{
printf("队列为空!\n");
return;
}
//pDel指向队头元素,由于队头指针front指向头结点,所以pDel指向头结点的下一个结点
LinkQueueNode* pDel = LQ->front->_next;
*data = pDel->_data; //将要出队的元素赋给data
LQ->front->_next = pDel->_next; //使指向头结点的指针指向pDel的下一个结点
//如果队列中只有一个元素,将队列置空
if (LQ->rear = pDel)
{
LQ->rear = LQ->front;
}
free(pDel); //释放pDel指向的空间
}
//取队头元素
int GetHead(LinkQueue* LQ, DataType* data)
{
if (IsEmpty(LQ))
{
printf("队列为空!\n");
return 0;
}
LinkQueueNode* pCur;
pCur = LQ->front->_next; //pCur指向队列的第一个元素,即头结点的下一个结点
*data = pCur->_data; //将队头元素值赋给data
return *data; //返回队头元素值
}
//清空队列
void ClearQueue(LinkQueue* LQ)
{
while (LQ->front != NULL)
{
LQ->rear = LQ->front->_next; //队尾指针指向队头指针的下一个结点
free(LQ->front); //释放队头指针指向的结点
LQ->front = LQ->rear; //队头指针指向队尾指针
}
}
//打印队列中的元素
void PrintLinkQueue(LinkQueue* LQ)
{
assert(LQ);
LinkQueueNode * pCur;
pCur = LQ->front->_next;
while (pCur)
{
printf("%-3d", pCur->_data);
pCur = pCur->_next;
}
printf("\n");
}
int main()
{
LinkQueue LQ;
DataType data;
//初始化队列
InitLinkQueue(&LQ);
//入队
EnterLinkQueue(&LQ, 1);
EnterLinkQueue(&LQ, 2);
EnterLinkQueue(&LQ, 3);
EnterLinkQueue(&LQ, 4);
EnterLinkQueue(&LQ, 5);
EnterLinkQueue(&LQ, 6);
EnterLinkQueue(&LQ, 7);
EnterLinkQueue(&LQ, 8);
printf("队列中的元素为:");
//打印队列中元素
PrintLinkQueue(&LQ);
printf("\n");
//取队头元素
data = GetHead(&LQ, &data);
printf("队头元素为:%d\n", data);
printf("\n");
//出队
DeleteLinkQueue(&LQ, &data);
printf("出队的元素为:%d\n", data);
printf("\n");
printf("队列中的元素为:");
PrintLinkQueue(&LQ);
printf("\n");
data = GetHead(&LQ, &data);
printf("队头元素为:%d\n", data);
printf("\n");
ClearQueue(&LQ);
system("pause");
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
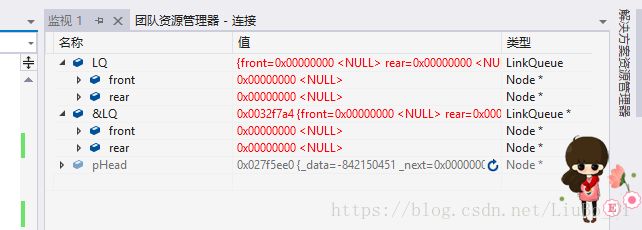
链式队列的结点是动态开辟的,入队时,为新节点开辟空间,出队使释放出队元素结点的空间。所以相对于顺序队列和循环队列,链式队列没有判断队列是否为满操作。但在清空队列时需要将队列所有结点的空间动态释放,从而防止内存泄露。测试清空函数可以通过编译器调试来观察。如下图:
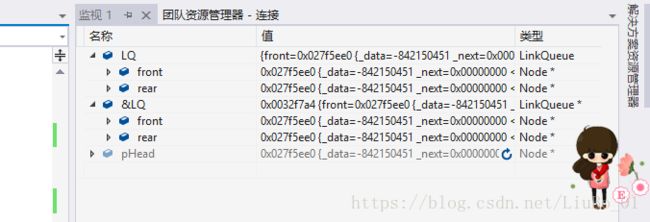
在执行完初始化后,开辟了一个新的结点pHead,使头指针和尾指针都指向pHead,pHed->-next = NULL;可以看到pHead的和fornt,rear的地址相同,没有执行入队操作,所以他们的数据域为一个随机值,指针域为空。
执行完两次入队后:
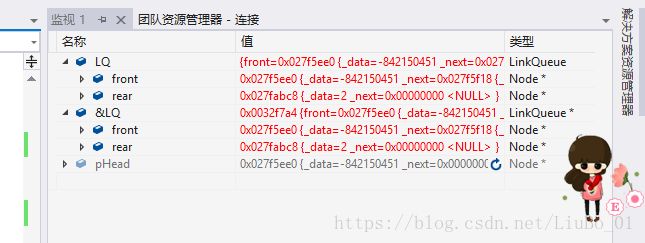
执行完清空操作后: