==========================2014.09.30更新============================
晕。。。今天看《数据结构与算法分析:C语言描述》练习题4.33, 发现各个结点的横坐标只要按照中序遍历的顺序就可以确定了,也就是说我写的那一堆“碰撞处理”什么的都是没有必要的。。。不过文章我就不改了,好歹也算是我自己独立想出来的解决方法,虽然弄得太复杂了点 。这件事充分说明了得多读书啊~
===================================================================
树是一种非线性结构,书上在讲解树的时候也都基本上会给出形象的树形图。但是当我们自己试着实现某种树,在调试、输出的时候确只能以字符的形式顺序地输出。这给调试等方面带来了很大的不便。比如想自己实现一个Binary Search Tree, 怎么知道我创建的树是否正确呢?当删除一个元素之后,怎么知道有没有破坏树的性质呢?一般我是先手画出正确的树结构,然后按照层次遍历的顺序将树输出,再和手画的图比较,判断是否正确。但是每次都需要手画的话十分不方便,所以我就想着写一个程序可以图形化地将树画出来。这个想法已经有了很久,但是一直拖延着没有真正动手实现。前几天下定决心要一鼓作气实现这个功能,这两天终于实现了,目前支持整数、字符还有字符串的输出,效果如下:

图 1

图 2
上图中的树是Binary Search Tree,都是随机生成的。程序是使用标准C++写的,图形的输出使用的全部是标准库中的函数。
下面就介绍一下程序的实现方式。要实现二叉树的可视化显示,需要考虑以下几个问题:
1、 如何判断每个节点应该在第几行输出,或者说输出的时候如何判断该换行?
2、 如何安排节点的位置,使左右孩子在其父节点的两边,以便直观地看出各个节点之间的关系?
3、 因为没有使用图形库,不能在任意位置输出,所以输出必须是一次性的,也就是在输出前就得确定图中所有字符应在的位置。
4、 通用性:
我写这个程序的目的是为了方便调试二叉树程序。为了输出一棵树,免不了要遍历这棵树,要遍历一棵树程序中就得访问一个节点的孩子,而不同二叉树节点的定义可能是不同的,节点中指向左孩子的指针名可能是left, 也可能是left_child。不能因为名字换了就得重新改写程序。
下面我就按照上面四个问题的顺序依次记录一下我的解决方法。
一、层次化输出
先不考虑问题2,对于给定一棵树,如何实现在输出时使不同层的节点在不同行呢?比如对于图3这棵树,其输出应为:
324
71, 776
43, 159, 425, 817
389

图 3
可以发现和普通的层次遍历:324, 71, 776,43, 159, 425, 817, 389 的区别就是在每层的最后一个节点后换个行。我们只需要在对树进行层次遍历,然后在输出每层最后一个节点之后再输出一个换行符即可。如何知道每层的最后一个结点是哪个呢?如果我们知道每一层一共有多少个节点,然后在输出的时候对已输出结点计数,就可以知道每层的最后一个结点是哪个。对于任意的一颗二叉树,我们虽然不知道任意一层的结点总数,但是我们知道第0层一定只有一个结点,就是根节点,第1层结点总数就是根结点的孩子结点总数,第2层结点总数就是第1层所有节点的孩子总数,以此类堆就可以知道所有层的结点总数,然后实现按层换行。下面是C++代码:
void traverse_level(TreeNode *root)
{
if (root == 0) {
return;
}
std::queue qnodes;
std::vector num_nodes; // num_nodes[i] : 第i层结点总数
num_nodes.push_back(1); // 第0层结点个数
num_nodes.push_back(0);
int n = 0, depth = 0;
for (qnodes.push(root); !qnodes.empty(); qnodes.pop()) {
TreeNode *temp = qnodes.front();
std::cout << temp->val << " ";
if (temp->left) {
qnodes.push(temp->left);
num_nodes[depth+1]++;
}
if (temp->right) {
qnodes.push(temp->right);
num_nodes[depth+1]++;
}
// 当前层最后一个节点
if (++n == num_nodes[depth]) {
n = 0;
depth++;
num_nodes.push_back(0);
std::cout << std::endl;
}
}
}
二、确定相对位置
层次化输出之后,下一步就是考虑如何解决问题2了,也就是安排结点的位置,使我们可以方便地看出结点之间的关系。先来看图4这种比较简单的情况:
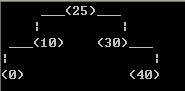
图 4
可以先不考虑画边沿,仅仅输出下图这个样子:
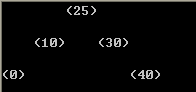
图 5
我的思路是这样的:
在节点类型中增加一个成员变量int pos;表示节点所在的位置,实际实现我是定义了一个基类,让树节点继承这个基类。先初始化根节点的pos为0,然后以层次遍历的顺序依次设置每个结点的pos值。因为是层次遍历,所以在设置某一个结点N时,它的父节点P一定已经设置好了,然后按照这个规则设置N的pos: 如果N是P的左孩子,则N.pos = P.pos - 1, 如果N是P的右孩子,则N.pos = P.pos + 1。这样处理后左子树中一定存在pos值为负数的节点,假设为-M,然后我们再将所有节点的pos都加上M,。经过上面的过程,上面的树中各个结点的pos值如下,下图中的数值代表的是结点的pos成员变量的值。
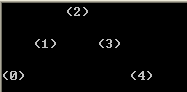
图 6
不考虑节点本身所占用的字符长度,规定每条边沿长度为L,则每个节点的位置即为L * pos。当然实际输出的时候是需要考虑节点本身占用的字符宽度的,这里就略去不谈了。
三、输出冲突
如下图7这棵树,按照上面的计算,值为90的节点和值为140的节点的pos值都是1,如果直接根据pos值计算输出位置的话,二者就会重叠在一起。还有种情况就是原本应该在左边的结点比在右边的结点的pos值大,这样也会造成冲突。下面介绍我的冲突解决方法。
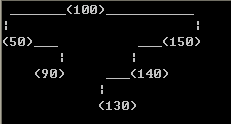
图 7
对已一个节点P,定义它的左子树中的结点pos最大值设为LMax(P),右子树中节点pos最小值为RMin(P)。 输出一棵树时不会有冲突的充分条件是对于每一个结点P都有:LMax(P) < P.pos < RMin(P),也就是所有左子树中的结点都在根节点的左方,所有右子树中的结点都在根结点的右方。
如果某一结点不满足LMax(P)
移动之后有两种情况,一种是结点P是其父节点(PP)的左孩子,这是P和P的右子树都属于PP的左子树,移动P和P的右子树有可能会造成条件LMax(PP) < P.pos的失败,所以这个时候需要对PP再进行一次冲突判断,这样递归向上知道没有冲突。第二种情况是P是PP的右孩子,这种情况下移动P和右子树肯定不会造成PP的冲突。在P的祖父节点中,设第一个具有左孩子的节点为A,移动P和P的右子树有可能造成A的冲突,需要再对A进行冲突处理。整个过程的伪代码如下。
CollisonProcess(node):
p = FirstAncestorWithLeftChild(node)
if MaxPos(node->left) >= node->pos
node->pos += MaxPos(node->left) - node->pos + 1
foreach child in node->right
child->pos += MaxPos(node->left) - node->pos + 1
CollisionProcess(p)
if MinPos(node->right) <= node->pos
foreach child in node->right
child->pos += node->pos - MinPos(node-right) + 1
CollisionProcess(p)
四、输出
经过了上面的处理之后,现在各个结点的pos值已经没有冲突了,只需要更具pos值输出各个结点即可。
具体的一些细节就不说了。
五、通用性
额。。。不想写了。。。这么说吧,今天我定义了一个树结点类型SA,其中指向孩子、父亲的指针名叫做left,right,parent,保存数据的成员变量名叫value。过了几天我又定义了一个树结点类型SB,其中指针名、数据名可能又成了lChild,rChild, parent,val,我怎么能让我的程序可以同时不管这些细节,对两种类型都能用呢?可以使用C++中的Pointer to Data Members。关于Pointer to Data Members可以参考《深度探索C++对象模型》中的3.6节,在google中搜索关键字Pointer to Data Members也可以搜到很多资料。
六、C++完整代码
自己都感觉代码写的好丑啊。。。。
因为需要多次用到层次遍历,所以我将层次遍历的代码单独作为一个模板函数写的,vst是对每个节点的操作
PosSetter.h:用来初始化每个树节点成员变量pos(继承自class InfoH),在函数VisualTree::draw()中被调用:
#ifndef POS_SETTER_H
#define POS_SETTER_H
#include "InfoH.h"
template
class PosSetter
{
public:
PosSetter(TreeNode* TreeNode::* p, TreeNode *TreeNode::* l, TreeNode *TreeNode::* r) :
parent(p), left(l), right(r)
{
}
void operator() (TreeNode *node)
{
TreeNode *p = node->*parent;
if (p != NULL) {
if (node == p->*left) { node->pos = p->pos - 1; }
if (node == p->*right) { node->pos = p->pos + 1; }
}
}
private:
TreeNode *TreeNode:: *parent;
TreeNode *TreeNode:: *left;
TreeNode *TreeNode:: *right;
};
#endif // POS_SETTER_H
PosAdder.h用来调整结点的pos值,调整值在实例化对象的时候指定,每个对象对应一个值。
#ifndef POS_ADDER_H
#define POS_ADDER_H
#include "InfoH.h"
class PosAdder
{
public:
PosAdder(int n_) : n(n_) {}
int operator() (InfoH *node) { return node->add_pos(n); }
private:
int n;
};
#endif // POS_ADDER_H
ExtremumGetter.h是用来在遍历结点的时候, 记录下节点中的极值的。
#ifndef EXTREMUM_GETTER_H
#define EXTREMUM_GETTER_H
template
class ExtremumGetter
{
public:
ExtremumGetter(TreeNode *min = 0, TreeNode *max = 0) {
init(min, max);
}
void operator() (TreeNode *p) {
if ((min_ && p->pos < min_->pos) || !min_) { min_ = p; }
if ((max_ && p->pos > max_->pos) || !max_) { max_ = p; }
}
void init(TreeNode *min, TreeNode *max) {
min_ = min; max_ = max;
if (min_ && max_ && max_->pos < min_->pos) {
std::swap(min_, max_);
}
}
TreeNode *min() const { return min_; }
TreeNode *max() const { return max_; }
private:
TreeNode *min_;
TreeNode *max_;
};
#endif // EXTREMUM_GETTER
以上三个文件中定义的三个类都重载了operator (),他们都是在调用VisualTree::traverse_level()的时候最为函数对象被调用的。
InfoH类是树节电要继承的类,定义了成员变量po
#ifndef INFOH_H
#define INFOH_H
#define INFI ((unsigned int)-1)
struct InfoH {
int pos;
bool newline;
InfoH() : pos(INFI), newline(false) {}
int add_pos(int add) {
pos += add;
return pos;
}
};
#endif
VisualTree.h:
#include
#include
#include
#include
#include
#include
#include "ExtremumGetter.h"
#include "PosAdder.h"
#include "PosSetter.h"
#include "TreePrinter.h"
struct IntExtremumPair {
int min;
int max;
IntExtremumPair(int rh1 = 0, int rh2 = 0) : min(rh1), max(rh2) {}
};
template
class VisualTree
{
public:
typedef TreeNode *TreeNode::* PtrToMember;
typedef ValueType TreeNode::* PtrToData;
VisualTree(PtrToMember p, PtrToMember lc, PtrToMember rc, PtrToData val);
void draw(TreeNode *node, const char *promot = NULL);
private:
void adjust_pos(TreeNode *root);
TreeNode* ancestor(TreeNode *node);
int digits(int n);
int digits(char c);
int digits(const char*s);
IntExtremumPair extreme_pos(TreeNode *p);
ExtremumGetter extreme_node(TreeNode *root);
int scan_tree(TreeNode *root);
template void traverse_level(TreeNode *p, VST &vst);
ExtremumGetter getter;
TreePrinter printer;
PosSetter setter;
PtrToMember parent, left, right;
ValueType TreeNode:: *value;
};
/*
* 构造函数
*/
template
VisualTree::VisualTree(PtrToMember p, PtrToMember lc, PtrToMember rc, PtrToData val) :
getter(), printer(p,lc,rc,val), setter(p,lc,rc), parent(p), left(lc), right(rc), value(val)
{
}
/*
* 越界调整
*/
template
void VisualTree::adjust_pos(TreeNode *root)
{
if (root == NULL) {
return;
}
int diff = 0;
IntExtremumPair extr;
if (root->*left) {
extr = extreme_pos(root->*left);
if (root->pos <= extr.max) { // 左子树越界:将根节点右移及其右子树右移
diff = extr.max - root->pos + 1;
PosAdder adder(diff);
root->add_pos(diff);
traverse_level(root->*right, adder);
adjust_pos(ancestor(root));
}
}
if (root->*right) { // 右子树越界:将右字树右移
extr = extreme_pos(root->*right);
if (extr.min <= root->pos) {
diff = root->pos - extr.min + 1;
PosAdder adder(diff);
traverse_level(root->*right, adder);
adjust_pos(ancestor(root));
}
}
}
/*
* 寻找节点node的第一个具有左孩子的祖先
* @return 祖先地址或者NULL
*/
template
TreeNode *VisualTree::ancestor(TreeNode *node)
{
TreeNode *pchild = node;
TreeNode *pparent = node->*parent;
while (pparent && pchild == pparent->*right) {
pchild = pparent;
pparent = pchild->*parent;
}
return pparent;
}
/*
* 计算一个整数n输出时占用的字符数
* @return 整数n输出时所占字符数
*/
template
int VisualTree::digits(int n)
{
int len = 0;
if (n < 0) {
len++;
n = -n;
}
do {
len++;
n /= 10;
} while (n);
return len;
}
/*
* 输出一个字符所占用的字符数
* @return 1
*/
template
int VisualTree::digits(char c)
{
return 1;
}
/*
* 输出一个字符串所占用的字符数
* @return 字符串长度
*/
template
int VisualTree::digits(const char *s)
{
return strlen(s);
}
/*
* 图形化显示二叉树
* @input root:树的根节点,promot:可选提示信息,应以'\0'结尾
*/
template
void VisualTree::draw(TreeNode *root, const char *promot)
{
if (promot) {
printf("%s\n", promot);
}
if (root == NULL) {
printf("Empty tree!\n");
return;
}
int len = scan_tree(root);
printer.set_edge_length(len);
traverse_level(root, printer);
}
/*
* 获得最靠左和最靠右的两个节点指针
* @return std::pair, 其中first指向最左节点,second指向最右节点
*/
template
ExtremumGetter
VisualTree::extreme_node(TreeNode *node)
{
getter.init(node, node);
traverse_level(node, getter);
return getter;
}
/*
* 获得最靠左的节点和最靠右的节点pos
* @return 包含最小/最大位置坐标的IntExtremumPair
*/
template
IntExtremumPair VisualTree::extreme_pos(TreeNode *node)
{
ExtremumGetter nodes = extreme_node(node);
IntExtremumPair ret;
if (nodes.min()) { ret.min = nodes.min()->pos; }
if (nodes.max()) { ret.max = nodes.max()->pos; }
return ret;
}
/*
* 扫描整棵树,设置相关信息(换行标记/数据位数)
* @return 最大数据位数
*/
template
int VisualTree::scan_tree(TreeNode *root)
{
int cnt; // 当前深度已扫描节点个数
int depth; // 当前扫描深度
int max_len;
std::queue qnode;
std::vector num_node; // num_node[i]: 深度为i的节点总数
num_node.push_back(1); // 一个根节点
num_node.push_back(0); // 初始化第1层
qnode.push(root);
// 将根节点位置设为0,据此算出其他节点相对位置
root->pos = 0;
traverse_level(root, setter);
// 获取最左最右坐标
IntExtremumPair extr = extreme_pos(root);
// 将最左节点坐标调整为0,其他节点整体右移
PosAdder adder(root->pos - extr.min);
traverse_level(root, adder);
cnt = 0; depth = 0; max_len = 0;
for ( ; !qnode.empty(); qnode.pop()) {
TreeNode *temp = qnode.front();
adjust_pos(temp);
if (temp->*left) {
qnode.push(temp->*left);
num_node[depth+1]++;
}
if (temp->*right) {
qnode.push(temp->*right);
num_node[depth+1]++;
}
if (++cnt == num_node[depth]) {
temp->newline = true;
depth++;
num_node.push_back(cnt = 0); // 初始化下下层节点个数
} else {
temp->newline = false;
}
max_len = std::max(max_len, digits(temp->*value));
}
// 使树和屏幕左侧之间不留空隙
extr = extreme_pos(root);
if (extr.min > 0) {
PosAdder adder(-extr.min);
traverse_level(root,adder);
}
return max_len;
}
/*
* 层次遍历二叉树,对树中每个节点执行操作vst
*/
template
template
void VisualTree::traverse_level(TreeNode *root, VST &vst)
{
if (root == NULL) {
return;
}
TreeNode *temp;
std::queue qnode;
for (qnode.push(root); !qnode.empty(); qnode.pop()) {
temp = qnode.front();
vst(temp);
if (temp->*left) { qnode.push(temp->*left); }
if (temp->*right) { qnode.push(temp->*right); }
}
}
TreePrinter.h:
#ifndef TREE_PRINTER_H
#define TREE_PRINTER_H
template
class TreePrinter
{
public:
typedef TreeNode *TreeNode::*PtrToMember;
typedef ValueType TreeNode::*PtrToData;
TreePrinter(PtrToMember p, PtrToMember l, PtrToMember r, PtrToData d) :
edge_len(2), num_out(0), vec(), parent(p), left(l), right(r), value(d)
{
}
void set_edge_length(int len)
{
edge_len = std::max(len, 2); // 边沿最小宽度为2
}
void operator() (TreeNode *node)
{
assert(node);
TreeNode *lc = node->*left;
TreeNode *rc = node->*right;
int lbl = 0, rbl = 0; // 左边沿字符长度,右边沿字符长度
int spaces = node->pos * edge_len - num_out; // 占位空白字符数
if (lc) { lbl = edge_len * (node->pos-(node->*left)->pos) - 1; }
if (rc) { rbl = edge_len * ((node->*right)->pos-node->pos) - 1; }
spaces -= lbl;
assert(spaces >= 0);
while (spaces--) {
num_out += printf(" ");
}
if (node->*left) {
vec.push_back(num_out-1);
while (lbl--) {
num_out += printf("_");
}
}
num_out += out_value(node->*value);
if (node->*right) {
while (rbl--) {
num_out += printf("_");
}
vec.push_back(num_out);
}
if (node->newline) {
new_line();
}
}
private:
int out_value(char c) { return printf("%c", c); }
int out_value(int i) { return printf("%d", i); }
int out_value(const char *p) { return printf("%s", p); }
void new_line()
{
printf("\n");
if (!vec.empty()) {
int n = 0, end = vec[vec.size()-1];
for (int i = 0; i <= end && n < (int)vec.size(); ++i) {
if (i == vec[n]) {
printf("|");
n++;
} else {
printf(" ");
}
}
}
printf("\n");
num_out = 0;
vec.clear();
}
int edge_len;
int num_out; // 已输出字符数
std::vector vec;
PtrToMember parent;
PtrToMember left;
PtrToMember right;
ValueType TreeNode:: *value;
};
#endif // TREE_PRINTER_H
下面的文件是我的测试文件,bst.h是我为了方便测试写的一个Binary Search Tree,在main.cc中想BST中随机插入一定数量的结点,然后显示:
bst.h:
#ifndef BST_H // binary search tree
#define BST_H
#include
#include // swap
#include "src/InfoH.h"
#define IS_ROOT(p) ((p)->parent == NULL)
#define IS_LEAT(p) ((p)->left == NULL && (p)->right == NULL)
#define IS_LEFT(p) (!IS_ROOT(p) && (p) == (p)->parent->left)
#define IS_RIGHT(p) (!IS_ROOT(p) && (p) == (p)->parent->right)
template
struct TreeNode : public InfoH {
T val;
TreeNode *parent;
TreeNode *left;
TreeNode *right;
TreeNode(const T &v) : InfoH(), val(v), parent(0), left(0), right(0) {}
TreeNode(const T &v, TreeNode *p) : InfoH(), val(v), parent(p), left(0), right(0) {}
};
template
class BSTree
{
public:
/*
* 构造函数
*/
BSTree() : root_(0) {}
/*
* 析构函数
*/
virtual ~BSTree()
{
while (!empty()) {
remove(root_);
}
}
/*
* 判断树是否为空
* @return true:空, false:非空
*/
bool empty()
{
return root_ == NULL;
}
/*
* 插入一个新节点
* @return 新插入节点地址
*/
TreeNode *insert(const T &val)
{
if (root_ == NULL) {
return root_ = new TreeNode(val);
}
TreeNode *parent = root_;
TreeNode *hole = 0;
hole = (root_->val < val ? root_->right : root_->left);
while (hole != NULL) {
parent = hole;
hole = (hole->val < val ? hole->right : hole->left);
}
if (parent->val < val) {
return parent->right = new TreeNode(val, parent);
} else {
return parent->left = new TreeNode(val, parent);
}
}
/*
* 寻找值为x的节点
* @reutrn 节点地址,如果不存在返回NULL
*/
TreeNode *find(T &x)
{
TreeNode *temp = root_;
while (temp != NULL) {
if (temp->val == x) {
break;
}
temp = (temp->val < x ? temp->right : temp->left);
}
// temp == NULL
return temp;
}
/*
* 删除指定节点
*/
void remove(TreeNode *p)
{
assert(p != NULL);
TreeNode *temp = NULL;
if (p->left && p->right) { // 有两个孩子
TreeNode *temp = succ(p);
std::swap(p->val, temp->val); // 交换和后继节点的内容
remove(temp); // 删除后继节点
} else if (p->left || p->right) { // 只有一个孩子
temp = (p->left ? p->left : p->right);
if (IS_ROOT(p)) {
root_ = temp;
root_->parent = NULL;
} else if (IS_LEFT(p)) {
p->parent->left = temp;
temp->parent = p->parent;
} else {
p->parent->right = temp;
temp->parent = p->parent;
}
delete p;
} else { // 没有孩子
if (IS_ROOT(p)) {
root_ = NULL;
} else if (IS_LEFT(p)) {
p->parent->left = NULL;
} else {
p->parent->right = NULL;
}
delete p;
}
}
/*
* 返回根节点地址
*/
TreeNode *root() const
{
return root_;
}
private:
/*
* 寻找最小节点
* @reutrn 最小节点地址
*/
TreeNode *min_node(TreeNode *p)
{
assert(p != NULL);
TreeNode *temp = p;
while (temp->left != NULL) {
temp = temp->left;
}
return temp;
}
/*
* 寻找最大节点
* @return 最大节点地址
*/
TreeNode *max_node(TreeNode *p)
{
assert(p != NULL);
TreeNode *temp = p;
while (temp->right != NULL) {
temp = temp->right;
}
return temp;
}
/*
* 寻找指定节点p的后继节点(比p节点大的所有节点中的最小节点)
* @return 后继节点地址
*/
TreeNode *succ(TreeNode *p)
{
assert(p != NULL);
if (p->right) { // 节点有右子树:右子树中最小节点即为后继节点
return min_node(p->right);
}
// else
TreeNode *child = p;
TreeNode *father = p->parent;
while (father && !IS_LEFT(child)) { // 节点无右子树:第一个有左孩子的祖先节点即为后继节点
child = father;
father = child->parent;
}
return father;
}
TreeNode *root_;
};
#endif
main.cc:
#include
#include
#include "bst.h"
#include "src/VisualTree.h"
int main(int argc, char*argv[])
{
typedef int ValueType;
typedef TreeNode NodeType;
BSTree tree;
VisualTree vtree(&NodeType::parent,
&NodeType::left,
&NodeType::right,
&NodeType::val);
int num = 15;
srand(time(NULL));
for (int i = 0; i < num; ++i) {
ValueType v = rand() % 1000; // 随机生成一个[0,1000)的数
tree.insert(v);
std::cout << "insert : " << v << std::endl;
vtree.draw(tree.root());
}
return 0;
}






