一、十进制整数转二进制
1.十进制整数转换为二进制整数采用除2取余,逆序排列法。具体做法是:
- 用2整除十进制整数,可以得到一个商和余数;
- 再用2去除商,又会得到一个商和余数,如此进行,直到商为0时为止
- 然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
例如 5 的二进制表示为:101
5 / 2 => 商2 余 1
2 / 2 => 商1 余 0
1 / 2 => 商0 余 1
2.二进制转十进制整数
从右向左用二进制数的每个位上数去乘以2的相应次方,并将所有结果相加。例如5的二进制是:101
1 * 2^0 = 1
0 * 2^1 = 0
1 * 2^2 = 4
相加就等于5
3.十进制小数转换为二进制小数
什么是二进制的小数? 就是形如101.11数字,注意,这是二进制的,数字只能是0和1。
101.11就等于 1 * 2^2 + 0 *2^1 + 1*2^0 + 1*2^-1 + 1*2^-2 = 4+0+1+1/2+1/4 = 5.75
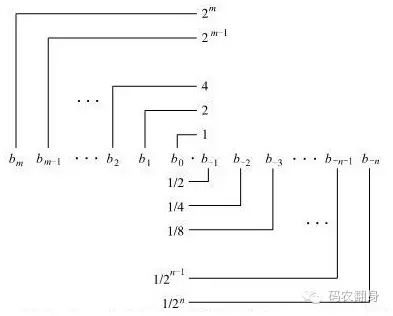
下面的图展示了一个二进制小数的表达形式。
从图中可以看到,对于二进制小数,小数点右边能表达的值是 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128 … 1/(2^n)
4.计算机存储十进制小数时需要先将其转为二进制小数,具体的转换方式是:
- 整数部分采用十进制转二进制方法进行
- 小数部分乘以2,然后取整数部分。不断重复该操作直到小数部分为0,或达到指定的精度。
举个例子:1.8125 转为 二进制小数
整数部分为1 转为二进制为 1
0.8125 x 2 1.625 取 1
0.625 x 2 1.25 取 1
0.25 x 2 0.5 取 0
0.5 x 2 1.0 取 1
最终1.8125的二进制是1.1101
但问题在于,不是所有的小数都能转换有限位数的二进制小数。例如10进制0.2的2进制:
0.2 x 2 0.4 0
0.4 x 2 0.8 0
0.8 x 2 1.6 1
0.6 x 2 1.2 1
0.2 x 2 0.4 0
0.4 x 2 0.8 0
0.8 x 2 1.6 1
0.6 x 2 1.2 1
……
发现了吗?它是乘不尽的,是无限循环(0011)的……
在计算机中,浮点数没有办法精确表示的根本原因在于计算机有限的内存无法表示无限的小数位。只能截断,截断就造精度的缺失。
0.2 的二进制小数表示可以是:
0.2 = 0.00110011
转为十进制为:1/8 + 1/16 + 1/128 + 1/256 = 0.19921875
已经很接近了,如果需要更精确的表示,只需要保留更长的有效位数。这也是双精度的double比单精度的float更精确的原因。
浮点数存储
C语言和C#语言中,对于浮点类型的数据采用单精度类型(float)和双精度类型(double)来存储,float数据占用32bit,double数据占用64bit,我们在声明一个变量float f= 2.25f的时候,是如何分配内存的呢?如果胡乱分配,那世界岂不是乱套了么,其实不论是float还是double在存储方式上都是遵从IEEE的规范的,float遵从的是IEEE R32.24 ,而double 遵从的是R64.53。
无论是单精度还是双精度在存储中都分为三个部分:
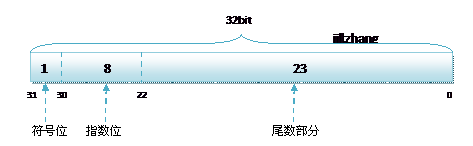
符号位(Sign) : 0代表正,1代表为负
指数位(Exponent):用于存储科学计数法中的指数数据,并且采用移位存储
尾数部分(Mantissa):尾数部分
其中float的存储方式如下图所示:
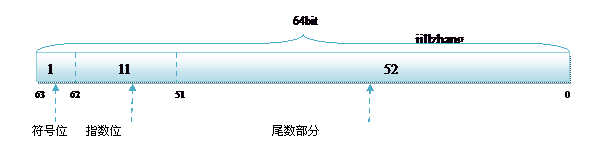
而双精度的存储方式为:
R32.24和R64.53的存储方式都是用科学计数法来存储数据的,比如8.25用十进制的科学计数法表示就为:8.25
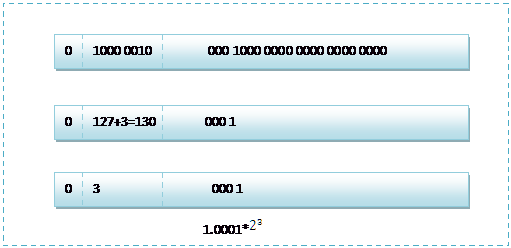
首先看下8.25,用二进制的科学计数法表示为:1.0001*[![clip_image002[2]](http://upload-images.jianshu.io/upload_images/1835466-495030f4ca32ff07.gif?imageMogr2/auto-orient/strip)](https://images.cnblogs.com/cnblogs_com/jillzhang/WindowsLiveWriter/float_A919/clip_image002%5B2%5D_1.gif)
按照上面的存储方式,符号位为:0,表示为正,指数位为:3+127=130 ,位数部分为,故8.25的存储方式如下图所示:
而单精度浮点数120.5的存储方式如下图所示:
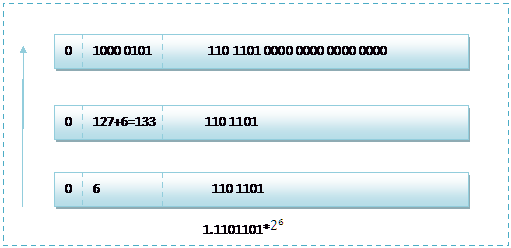
那么如果给出内存中一段数据,并且告诉你是单精度存储的话,你如何知道该数据的十进制数值呢?其实就是对上面的反推过程,比如给出如下内存数据:0100001011101101000000000000,首先我们现将该数据分段,0 10000 0101 110 1101 0000 0000 0000 0000,在内存中的存储就为下图所示:
[图片上传失败...(image-af8887-1513496425477)]
根据我们的计算方式,可以计算出,这样一组数据表示为:1.1101101*
而双精度浮点数的存储和单精度的存储大同小异,不同的是指数部分和尾数部分的位数。所以这里不再详细的介绍双精度的存储方式了,只将120.5的最后存储方式图给出,大家可以仔细想想为何是这样子的
下面我就这个基础知识点来解决一个我们的一个疑惑,请看下面一段程序,注意观察输出结果
float f = 2.2f;
double d = (double)f;
Console.WriteLine(d.ToString("0.0000000000000"));
f = 2.25f;
d = (double)f;
Console.WriteLine(d.ToString("0.0000000000000"));
可能输出的结果让大家疑惑不解,单精度的2.2转换为双精度后,精确到小数点后13位后变为了2.2000000476837,而单精度的2.25转换为双精度后,变为了2.2500000000000,为何2.2在转换后的数值更改了而2.25却没有更改呢?很奇怪吧?其实通过上面关于两种存储结果的介绍,我们已经大概能找到答案。首先我们看看2.25的单精度存储方式,很简单 0 1000 0001 001 0000 0000 0000 0000 0000,而2.25的双精度表示为:0 100 0000 0001 0010 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000,这样2.25在进行强制转换的时候,数值是不会变的,而我们再看看2.2呢,2.2用科学计数法表示应该为:将十进制的小数转换为二进制的小数的方法为将小数2,取整数部分,所以0.282=0.4,所以二进制小数第一位为0.4的整数部分0,0.4×2=0.8,第二位为0,0.82=1.6,第三位为1,0.6×2 = 1.2,第四位为1,0.2*2=0.4,第五位为0,这样永远也不可能乘到=1.0,得到的二进制是一个无限循环的排列 00110011001100110011... ,对于单精度数据来说,尾数只能表示24bit的精度,所以2.2的float存储为:
但是这样存储方式,换算成十进制的值,却不会是2.2的,应为十进制在转换为二进制的时候可能会不准确,如2.2,而double类型的数据也存在同样的问题,所以在浮点数表示中会产生些许的误差,在单精度转换为双精度的时候,也会存在误差的问题,对于能够用二进制表示的十进制数据,如2.25,这个误差就会不存在,所以会出现上面比较奇怪的输出结果。