算法设计方法2：分而治之

前言:分而治之策略不仅被君主和殖民者成功地用来统治殖民地，也可以用来设计有效的计算机算法。分而治之方法把一个问题的实例分解为若干个小型而独立的实例，从而可以在并行计算机的不同处理器上完成。分而治之方法可以解决如下问题:最大最小问题、矩阵乘法、一个娱乐数学—残缺棋盘问题、排序、选择和一个计算几何问题—在二维空间中寻找距离最近的两个点。

一、分而治之的概念

1、分而治之的定义

“分而治之”( Divide and conquer)方法(又称“分治术”) ，是有效算法设计中普遍采用的一种技术。

所谓“分而治之” 就是把一个复杂的算法问题按一定的“分解”方法分为等价的规模较小的若干部分，然后逐个解决，分别找出各部分的解，把各部分的解组成整个问题的解，这种朴素的思想来源于人们生活与工作的经验，也完全适合于技术领域。诸如软件的体系结构设计、模块化设计都是分而治之的具体表现。

分而治之方法与软件设计的模块化方法非常相似。为了解决一个大的问题，可以：

1) 把它分成两个或多个更小的问题；

2) 分别解决每个小问题；

3) 把各小问题的解答组合起来，即可得到原问题的解答。小问题通常与原问题相似，可以递归地使用分而治之策略来解决。

分而治之方法可以用于实现不同的排序方法，下面会介绍两种排序算法：快速排序（quick sort）和归并排序。

2、分而治之的核心

解决规模庞大的问题的有效方法之一，就是将其分解为若干规模更小的子问题，再通过递归机制分别求解。这种分解持续进行，直到子问题规模缩减至平凡情况。这也就是所谓的分而治之（divide-and-conquer）策略。

二、分而治之经典实例

1、找出假币

问题描述：一个袋子有16块硬币，其中可能有一个是假币，并且假币比真市要轻。现在要找出这个假币，而且有一台仪器可用来比较两组硬币的重量。

1）按照常规思路，可以得出一种方案：

比较硬币1和硬币2。如果硬币1比硬币2轻，则硬币1是假币。如果硬币2比硬币1轻，则硬币2是假币。假如两个硬币重量相等，则比较硬币3和硬币4。同样，如果有一个硬币轻一些，则寻找假币的任务完成。假如两个硬币重量相等，则继续比较硬币5和硬币6。以此方式类推，最多比较8次便可以确定是否存在假币，而且可以找到假币。

2）另一种方法是分而治之：

假设16个硬币是一个问题的大实例。第一步，把这个大实例分成两个或更多的小实例。把16个硬币随机分成两组A和B,每组有8个硬币。第二步，利用仪器确定哪一组有假币。 如果两组重量相等， 则无假币。如果不等，则可以确定假币存在，并且在较轻的那一组硬币中。 最后，第三步，从第二步的结果中得到解后再递归求解。在这个算法中，第三步是容易的。16枚硬币实例中只有一个伪币，当且仅当A或B有一个伪币。因此仅仅通过一次重量比较，就可以确定是否存在假币。

现在假设要找出假币。我们把两个或三个硬币视为不可再分的小实例。注意，只有一个硬币，不能确定它是否是假币。其他实例都是大实例。对于个小实例，用其中的一个硬币和其他最多两个硬币比较，最多比较两次就可以找到假币。

16个硬币是一个大实例。把它分成两个实例，A组和B组，每组有8个硬币。比较这两组的重量，可以确定是否存在假币。如果没有假币，则算法中止。否则继续划分。假设B组较轻，把B组分成两组B1和B2，每组有四个硬币。如果B1较轻，则假币在B1中。再将B1分成两组。B1a和B1，每组有两个硬币。继续比较，可以得到较轻的一组，它只有两个硬币，是一个小实例，不需要再细分。最后一次比较，较轻者就是假币。

2、金块问题

问题描述：一个老板有一 袋子金块。每个月有两名雇员会因其优异表现分别获一个金块的奖励。按规矩，排名第一名的雇员得到最重的金块，排名第二的雇员得到最轻的金块。因为有新的金块定期加入袋中，所以每个月都必须找出最轻和最重的金块。假设有一台比较重量的仪器，我们希望用最少的比较次数找出最重和最轻的金块。

1）逐个比较的常规方法

假设有n个金块。可以通过n-1次比较找到最重的金块。找到最重的金块后，可以从余下的n-1个金块中，用类似的方法，通过n -2次比较找出最轻的金块来。这样，总的比较次数为2n-3。

2）分而治之方法

当n很小时，比如说，n≤2,一次比较就足够了。当n较大时(n>2),第一步，把一袋金块平分成两个小袋金块A和B。第二步，分别找出在A和B中最重和最轻的金块。设A的最重和最轻的金块分别为Ha与La, B的最重和最轻的金块分别为 Hb和Lb。第三步，比较Ha和Hb,可以找到所有金块中最重的;比较La 和Lb,可以找到所有金块中最轻的。第二步可以递归地实现分而治之方法。

 假设n=8。把大袋子分为两个小袋子A和B，各有4个金块。为了在A中找出最重和最轻的金块，把A的4个金块分成两组A1和A2。每组有两个金块。通过一次比较可以在A1中找出较重的金块Ha1和较轻的金块La1,再通过一次比较，可以找出Ha2和La2。现在通过比较Ha1和Ha2,能找出Ha;通过La1和La2的比较可以找出La。这样，通过4次比较便可以找到Ha和La。同样，再通过4次比较可以确定Hb和Lb。现在，通过比较Ha和Hb(La和Lb)就能找出所有金块中最重(最轻)的。因此，当n=8时，分而治之方法需要10次比较。而常规方法2n-3需要13次比较。

很明显，使用分而治之方法比逐个比较的方法少用了25%的比较次数。

3、归并排序

①定义

归并排序(Merge Sort)，是建立在归并操作上的一种稳定的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。归并操作(merge)，也叫归并算法，指的是将两个顺序序列合并成一个顺序序列的方法,合并的前提是两个数组已经是有序的。

与快速排序思想类似：将待排序数据分成两部分，继续将两个子部分进行递归的归并排序；然后将已经有序的两个子部分进行合并，最终完成排序。其时间复杂度与快速排序均为O(nlogn)，但是归并排序除了递归调用间接使用了辅助空间栈，还需要额外的O(n)空间进行临时存储。从空间复杂度的角度归并排序略逊于快速排序，但归并排序是一种稳定的排序算法，快速排序则不然。

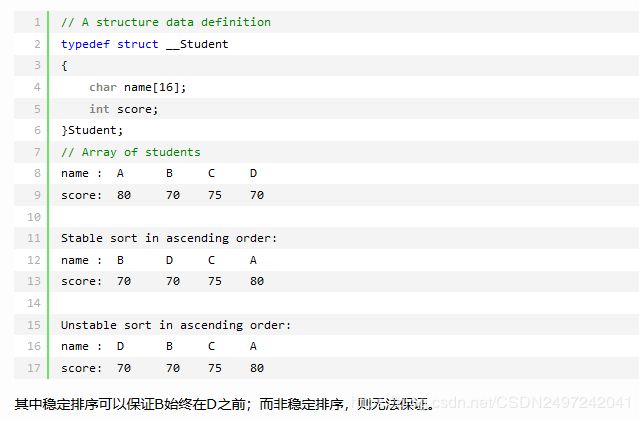
所谓稳定排序，表示对于具有相同值的多个元素，其间的先后顺序保持不变。对于基本数据类型而言，一个排序算法是否稳定，影响很小，但是对于结构体数组，稳定排序就十分重要。例如对于student结构体按照关键字score进行非降序排序。

归并排序举例：

如设有数列{6，202，100，301，38，8，1}

初始状态：6,202,100,301,38,8,1

第一次归并后：{6,202},{100,301},{8,38},{1}，比较次数：3；

第二次归并后：{6,100,202,301}，{1,8,38}，比较次数：4；

第三次归并后：{1,6,8,38,100,202,301},比较次数：4；

总的比较次数为：3+4+4=11；

②算法思想

• 把长度为n的输入序列分成两个长度为n/2的子序列；

• 对这两个子序列分别采用归并排序；

• 将两个排序好的子序列合并成一个最终的排序序列。

③Java代码

归并排序总体分为两步，首先分成两部分，然后对每个部分进行递归的归并排序，最后将已经有序的两个子部分进行合并。当然也可以分成三部分或其他，然而通常是分成两部分，因此又称为二路归并。归并操作其实就是前面我们学过的有序数组或者链表的合并。

/*
* K路划分，即将原序列划分为k个子序列，通常是二路划分(k>=2)
**/
private void MergeSort(int[] a, int left, int right) 
{
        //若数组大小为1，则算法中止；否则进行k路划分，先对每个子序列排序，最后将有序子序列归并
        if(a.length==1)
          return;

        //对数组a[left:right]排序
	if(left

对n个元素排序，一种最简单的方法是用链表存储元素。将链表在第(n/2)个节点处断开，分为个大致相等的子链表。归并过程将两个排序后的子链表归并在一 起。但是我们不使用链表因为我们要与堆排序和插入排序做性能比较，而后两种排序方法都不使用链表。
归并排序函数用一个数组a来存储元素序列E,并用a返回排序后的序列。当序列E划分为两个 子序列时，不必把它们分别复制到 A和B中，只需简单地记录它们在序列E的左右边界。 然后将排序后的子序列归并到一个新数组b中，最后再将它们复制回a中。分

④归并排序比较占用内存，但却是一种效率高且稳定的算法。改进归并排序在归并时先判断前段序列的最大值与后段序列最小值的关系再确定是否进行复制比较。如果前段序列的最大值小于等于后段序列最小值，则说明序列可以直接形成一段有序序列不需要再归并，反之则需要。所以在序列本身有序的情况下时间复杂度可以降至O(n)。

归并排序算法可以消除递归，用迭代的方法排序，这称为直接/自然归并排序，有兴趣可以了解一下。

4、快速排序

①定义

快速排序（Quicksort）是对冒泡排序的一种改进，时间复杂度为O(nlogn)，属于高效但不稳定的排序算法。

快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行递归排序，以达到整个序列有序。

快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：

• 从数列中挑出一个元素，称为 “基准/支点”（pivot）；

• 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；

• 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

②算法思想

在快速排序中，n 个元素被分成三段（组）：左段left，右段right 和中段middle。中段仅包含一个元素。左段中各元素都小于等于中段元素，右段中各元素都大于等于中段元素。因此left 和right 中的元素可以独立排序，并且不必对left 和right 的排序结果进行合并。middle 中的元素被称为支点( pivot )。

③伪代码

使用快速排序方法对a [ 0 : n- 1 ] 排序。

从a [ 0 : n- 1 ] 中选择一个元素作为middle，以该元素为支点把余下的元素分割为两段left 和right，使得left中的元素都小于等于支点，而right 中的元素都大于等于支点。

递归地使用快速排序方法对left 进行排序。

递归地使用快速排序方法对right 进行排序。

所得结果为left + middle + right。

考察元素序列[ 4 , 8 , 3 , 7 , 1 , 5 , 6 , 2 ]。

假设选择元素6 作为支点，则6 位于middle；4，3，1，5，2 位于l e f t；8，7 位于right。当left 排好序后，所得结果为1，2，3，4，5；当right 排好序后，所得结果为7，8。把right 中的元素放在支点元素之后，left 中的元素放在支点元素之前，即可得到最终的结果[ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 ]   。

④Java代码

package com.quicksort;
 
import java.util.Arrays;
 
public class QuickSort 
{
	public static void main(String[] args) 
        {
		int[] a = {1, 2, 4, 5, 7, 4, 5 ,3 ,9 ,0};
		System.out.println(Arrays.toString(a));
		quickSort(a);
		System.out.println(Arrays.toString(a));
	}
 
	public static void quickSort(int[] a) {
		if(a.length>0) {
			quickSort(a, 0 , a.length-1);
		}
	}
 
        /*
         *对数组a[low:high]进行快速排序
        */
	private static void quickSort(int[] a, int low, int high) 
        {
		//找到递归算法的出口
		if( low > high) 
		   return;
		
		int leftCursor = low;//从左到右移动的索引
		int rightCursor = high;//从右往左移动的索引
		int pivot = a[low];

		//将位于左侧不小于支点的元素和位于右侧不大于支点的元素进行交换
		while(true) 
                {
			//从左至右，寻找左侧不小于支点的元素
			while(a[leftCursor]pivot)
				rightCursor--;
			
			
			//交换位置
			if(leftCursor>=rightCursor) 
                            break;//leftCursor和rightCursor碰面了，意味着完成一趟排序
                        else
                        {
				int temp = a[i];
				a[i] = a[j];
				a[j] = temp;
			}
		}

		//放置支点
		a[low] = a[rightCursor];//此时rightCursor处就是支点的位置
                a[rightCursor] = pivot;
		
		quickSort(a, low, i-1 );//对key左边的数快排
		quickSort(a, i+1, high);//对key右边的数快排
	}
}

复杂度分析：

所需要的递归栈空间为0(n)。若使用栈来模拟递归，则需要的空间可以减少为O(logn)。在模拟过程中，首先对数据段left 和right中较小者进行排序，把较大者的边界放人栈中。
在最坏情况下，例如，数据段left总是空，这时的快速排序用时为O(n^2)。在最好情况下，即数据段left和right的元素数目总是大致相同，这时的快速排序用时为0(nlogn)。而快速排序的平均复杂度也是O(nlogn),这是令人惊奇的速度。

⑤快速排序优化

三平均分区法或三值取中快速排序

对有序的输人序列实施快速排序，却表现出最坏情况下的时间性能。也就是说，一个快速排序算法，它对有序表排序比对无序表排序要慢，这是让人痛苦的问题。不过，我们可以决这个问题，同时提高快速排序的平均性能，方法是根据三值取中规则( median-of-threede)选择支点元素。三值取中快速排序(median-of-three quick sor)在三元素a[leftEnd]、a[lefEnd+rightEnd)/2]和 a[rightEnd]中选择大小居中的中值元素作为支点无素。例如，若三元素分别为5,9.7,则取7为支点元素。

关于这一改进的最简单的描述大概是这样的：与一般的快速排序方法不同，它并不是选择待排数组的第一个数作为中轴，而是选用待排数组最左边、最右边和最中间的三个元素的中间值作为中轴。这一改进对于原来的快速排序算法来说，主要有两点优势：
　　（1） 首先，它使得最坏情况发生的几率减小了。
　　（2） 其次，未改进的快速排序算法为了防止比较时数组越界，在最后要设置一个哨点。