数据结构与算法分析之二叉树的三种遍历方式。--前序遍历,中序遍历和后序遍历
在介绍二叉树的遍历算法之前,我们需要介绍一下二叉树以及遍历方式这些概念。
二叉树:是树的一种特殊结构,在二叉树中每个结点最多只能有两个子节点。
二叉树中最重要的操作就是遍历,通常二叉树的遍历方式有一下几种:
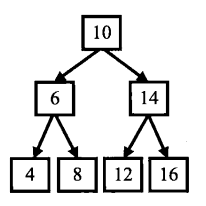
前序遍历:先访问根结点,再访问左结点,最后访问右结点。如图示前序遍历顺序是:10、6、4、8、14、12、16。(根结点在首位)
中序遍历:先访问左结点,再访问根结点,最后访问右结点。如图所示中序遍历顺序是:4 、6、 8 、10 、12 、14 、16 。(根结点在中间)
后序遍历:先访问左结点,再访问右结点,最后访问根结点。如图所示后序遍历顺序是:4、 8、 6 、12 、16 、14 、10。(根结点在最后)
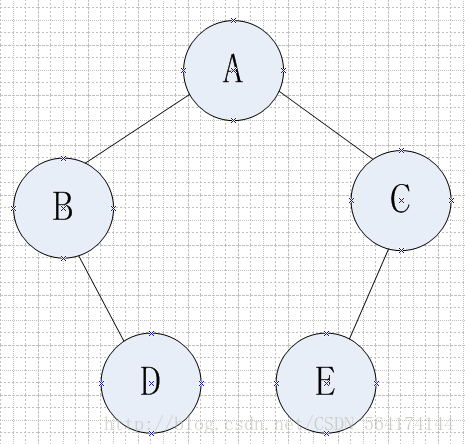
话不多说,直接上一道例题深刻了解二叉树的建立和遍历过程。题目:建立二叉树,并输出每个字符所在的层数。二叉树如下图所示:
如图所示,这是以个普通的二叉树。对于这道题,我的思路是这样的:
1、建立二叉树的结点,用结构体数据类型表示;
2、根据前序遍历的规则组建二叉树–用递归的方式完成二叉树的组建过程,其中传入的是结点所在位置的指针。
3、同样方式,用中序遍历和后序遍历输出结点排序。
详细叙述见下分析:
1、首先定义一个结构体,里面的数据包括二叉树每个结点的数据值,和指向左右结点的指针。定义这个数据结构体是为后面建立二叉树左准备:
typedef struct BiTNode
{
ElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;//这里的BiTNode==*BiTree2、二叉树结点已经建立了,下面我们需要做的就是把这些结点连接起来,生成一个特定的二叉树,下面根据本题所给条件,以先序遍历的方式,输入本题的二叉树序列,从而生成如图二叉树。这里注意使用的生成方式是递归生成二叉树,也就是把每个结点的左右指针连接到特定结点上,直至结束。
注意:因为只根据先序遍历一种方式建立二叉树,为了保证二叉树的唯一性,空缺子叶用空格符号代替。
void CreateBiTree(BiTree *T)
{
ElemType c;
scanf("%c",&c);
if(' '==c)
*T=NULL;
else
{
*T=(BiTree *)malloc(sizeof(BiTNode));
(*T)->data=c;
CreateBiTree(&((*T)->lchild));
CreateBiTree(&((*T)->rchild));
}
return ;
}注意:这里是传入的BiTree * T参数,是本题一个难点。首先这是一个创建二叉树的模块,简单讲就是每个结点按照一定规则连接在一起。若输入方式以先序遍历为例,每个结点就是按照先序遍历的方式连接。先访问根结点,再访问左树数,后访问右子树。每次递归这个函数,就会调用scanf函数,输入当前结点的值。(这里的scanf输入整个二叉树的节点值),包括不存在的子叶,用空格代替。因为无法获取下一个结点的数据,因此需要在递归过程中提前传入下个结点的地址。然后通过读地址进行操作。* T= (BiTree* )malloc(sizeof(BiTNode)) ; 此处强制类型转换,是因为T里面存放的是结构体的地*址,因此需要将右边也强制类型转换为结构体地址的类型。
3、在二叉树建立完成之后,需要开始二叉树的遍历工作。此处用到的也是递归操作,简单说就是每次处理一个结点。以先序遍历为例,先输出本结点的值,和深度信息,然后递归下个左结点的信息,然后是右结点的信息,按照这样的方式输出整个二叉树的结点信息。
同样方式去实现中序遍历和后序遍历。
//前序遍历二叉树
int visitnum=0;
void PreOrderTraverse(BiTNode *T,int level)
{
if( (bool&)T )
{
if(visitnum==0)
cout<<T->data<<" ";
else
visit(T->data,level);
PreOrderTraverse(T->lchild,level+1);
PreOrderTraverse(T->rchild,level+1);
}
visitnum=1;
return ;
}注意,进行遍历的过程,二叉树已经建立起来了。因此只需要指向结构体的指针即可,遍历操作运用到的是结构体数据,包括值和指针,直接用指针进行操作就可以了。
4、最后编写一个功能模块,去实现结点所在深度,只需要同时输出结点值和深度值即可。所以在实现时添加深度值。
具体代码如下:
/*
前序遍历:先访问根结点,在访问左子树,后访问右子树
中序遍历:先访问左子树,根结点,右子树
后续遍历:先访问左子树,然后右子树,根结点
*/
#includedata<<" ";
PreOrderTraverse(T->lchild,level+1);
PreOrderTraverse(T->rchild,level+1);
}
return ;
}
void PreOrderTraverseVisit(BiTNode *T,int level)//这里的指针,里面存放的就是结构体数据
{
if( (bool&)T )
{
visit(T->data,level);
PreOrderTraverseVisit(T->lchild,level+1);
PreOrderTraverseVisit(T->rchild,level+1);
}
return ;
}
//中序遍历二叉树
void MidOrderTraverse(BiTNode *T,int level)
{
if( (bool&)T )
{
MidOrderTraverse(T->lchild,level+1);
//visit(T->data,level);
cout<data<<" ";
MidOrderTraverse(T->rchild,level+1);
}
return ;
}
//后序遍历二叉树
void LastOrderTraverse(BiTNode *T,int level)
{
if( (bool&)T )
{
LastOrderTraverse(T->lchild,level+1);
LastOrderTraverse(T->rchild,level+1);
//visit(T->data,level);
cout<data<<" ";
}
return ;
}
int main()
{
int level=1;
BiTNode *T=NULL;
CreateBiTree(&T);
cout<<"前序二叉树遍历结果:"<cout<cout<<"中序二叉树遍历结果:"<cout<cout<<"后序二叉树遍历结果:"<cout<cout<<"各结点所在层数:"<cout<//PreOrderTraverse(T,level);
system("pause");
return 0;
} 注意:输入二叉树结点序列的时候一定要在无子叶的地方加上空格。
如:AB” “D” “” “CE” “” “” ”
输入结果如下: