Week 1 & Week 2 机器学习入门，线性回归案例和matlab实现

Week 1 & Week 2

摘要

Week 1 和Week 2介绍了机器学习的基础知识，分类和几个基本的概念。以线性回归开篇，用房价预测的具体案例，应用了这些概念。配套练习，则是使用Matlab对以上案例进行实现。感觉设计非常非常合理，比如损失函数，梯度下降，特征归一化，标准差，学习效率等等概念都手动进行实现。

当然，为了使用Matlab实现，课程也介绍了Matlab基础和Matrix线性代数基础知识。具体的实现难度，在于对公式的反复熟悉和公式转成代码，使用矩阵运算。

具体做的事，其实就是

基本概念

分类——监督学习 & 非监督学习

课中提到，数据有“right answer”的话，那么就是监督式学习。其实有些费解，比较好理解的是，目标分类未知，即类似聚类问题，就属于非监督，其他都是监督。但我认为这样并不太好，从ex1来看，建模的过程，“监督”大概就是指损失函数对函数本身的矫正，而损失函数的构建，正好需要我们去对比“正确答案”。

Hypothesis——H(x)：这是我们的目标函数

Cost function——J(θ)：损失函数，我们设置的H(x)和正确答案相差的量，具体如何设置，需要进行设计。

Gradient descent：梯度下降，这其实就是导数、偏导数的几何意义，寻找损失函数的最小值。

Feature normalization：归一化，特征如果取值范围差距很大的话，会严重影响梯度下降的效率，这个可以从等高线图看出来。

Normal Equation：求解最小值的另一种方法。线性代数利用公式直接求解方程。

Learning Rate：α值，梯度下降中的一个关键参数，影响到梯度下降的效率。

从线性回归讲起

这里使用的案例是已知一些特征，如占地，人口，卧室数量等，对房价进行预测。数学理论其实搞清楚，挺简单的。

这是目标函数，x为特征，这事只有一个特征的特殊情况，但是足够有代表性——多特征无非也就是增加θ和x而已。以下同理。表示特征和目标值之间是线性相关的关系。

$$H_{\theta }(x)={\theta }_0+{\theta }_{1}x$$

损失函数，设计思想是预测值与目标值的差距，平方消除正负性，前面的系数是为了求导方便。

$$J(\theta )=\frac{1}{2m}\cdot \sum _{i=1}^m{\left(H\left(x^{(i)}\right)-y^{(i)}\right)}^2$$

梯度下降，有点复杂，但其实就是损失函数对θ的偏导数，每次所有θ减少相应的偏导值。

$${\theta }_j={\theta }_j-\delta j={\theta }_j-\alpha \frac{\partial (J(\theta ))}{\partial {\theta }_j}={\theta }_j-\frac{1}{m}\alpha \sum _{i=1}^m\left(H_{\theta }\left(x^{(i)}\right)-y_i^i\right)x_j^{(i)}$$

迭代无数次之后，最终损失函数会达到最小，此时的θ也就是目标函数最佳拟合的取值。

Matlab实现

此部分，实现了上述的案例，所有基础概念都用代码进行实现。需要熟悉的知识有，Matlab的基本操作，矩阵运算的应用。

我认为，核心的方法是，把数学公式先转换成矩阵运算，再做实现。

要把目标函数转化成矩阵形式，需要处理第一个θ，构造矩阵X，假设只有二组数据。
$$X=\left[\begin{array}{ll}1& x_1\\ 1& x_2\end{array}\right]$$
目标函数从上方的数学公式转化成矩阵运算公式，下同。
$$H_{\theta }(x)={\theta }_0+{\theta }_{1}x$$

$$H_{\theta }(x)=\theta X$$

损失函数
$$J(\theta )=\frac{1}{2m}\cdot \sum _{i=1}^m{\left(H\left(x^{(i)}\right)-y^{(i)}\right)}^2$$

$$J(\theta )=\frac{1}{2m}(\theta X-y{)}^{\top }(\theta X-y)$$

实现代码

function J = computeCostMulti(X, y, theta)
    t=X*theta-y;
    J=(t'*t)/(2*m);
end

梯度下降
$${\theta }_j={\theta }_j-\delta j={\theta }_j-\alpha \frac{\partial (J(\theta ))}{\partial {\theta }_j}={\theta }_j-\frac{1}{m}\alpha \sum _{i=1}^m\left(H_{\theta }\left(x^{(i)}\right)-y_i^i\right)x_j^{(i)}$$

$$\theta =\theta -\frac{\alpha }{m}{X}^T(\theta X-y)$$

实现代码

function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters)
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);

for iter = 1:num_iters
    theta=theta-(X'*(X*theta-y))*alpha/m; 
    J_history(iter) = computeCostMulti(X, y, theta);

end
end

代码详解Github

附录 plot的不熟练语法整理

画散点图，参数为‘rx’，后面可边参数两个为一对

plot(x,y,'rx','MarkerSize',10)
ylabel('Profit in $10,000s'); % Set the y?axis label
xlabel('Population of City in 10,000s'); % Set the x?axis label

plot(X(:,2), X*theta, '-');
legend('Training data', 'Linear regression');

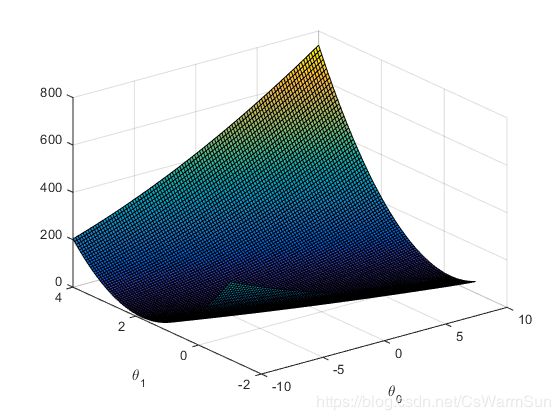
画面，要用到srf方法，需要传入x，y，z三轴的值

theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);
J_vals = zeros(length(theta0_vals), length(theta1_vals));

for i = 1:length(theta0_vals)
    for j = 1:length(theta1_vals)
	  t = [theta0_vals(i); theta1_vals(j)];    
	  J_vals(i,j) = computeCost(X, y, t);
    end
end
J_vals = J_vals';
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');

等高线，反直觉的也需要传入x，y，z，可以看作是上图的画法，但是调用contour函数，最后个参数，不知道具体内涵。

contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);