A*算法-第K短路

A*算法—第K短路

A* 算法（这里的* 英文就读作star），是一种启发式搜索的方法，它离我们并不遥远，常用的BFS就是A*算法的一种特例。

启发式搜索：

DFS与BFS都属于非启发式搜索，又称盲目型搜索，它们最大的不同就是启发式搜索的选择不是盲目的，可以通过一个启发函数进行选择。
现在看一下下面的两张图，就可以很形象的理解了：

假如正常的搜索方式，我们会不断移动，直至遇到障碍物，显然这种方法是很愚蠢的，但是正常的方法的确是这样进行的，那么我们就希望扩展一个运动算法，用于对付上图所示的障碍物。或者避免制造凹形障碍，或者把凹形出口标识为危险的(只有当目的地在里面时才进去):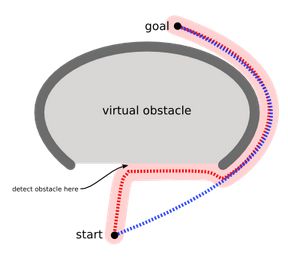

A*算法：

为启发式算法中很重要的一种，被广泛应用在最优路径求解和一些策略设计的问题中。而A*算法最为核心的部分，就在于它的一个估值函数的设计上：
f(n)=g(n)+h(n)
其中f(n)是每个可能试探点的估值，它有两部分组成：一部分为g(n)，它表示从起始搜索点到当前点的代价（通常用某结点在搜索树中的深度来表示）。另一部分，即h(n)，它表示启发式搜索中最为重要的一部分，即当前结点到目标结点的估值，h(n)设计的好坏，直接影响着具有此种启发式函数的启发式算法的是否能称为A*算法。

一种具有f(n)=g(n)+h(n)策略的启发式算法能成为A算法的充分条件是：

1. 搜索树上存在着从起始点到终了点的最优路径。
2. 问题域是有限的。
3. 所有结点的子结点的搜索代价值>0。
4. h(n) <= h * (n) （h*(n)为实际问题的代价值）。

一般的搜索前三条都可以满足，而第四点就要视情况而定了。
如果上面的概念不能很好理解也没关系，下面来看一道A*算法的经典题目，求第K短路【POJ2449】—— [ 题目链接 ]：

Description

“Good man never makes girls wait or breaks an appointment!” said the mandarin duck father. Softly touching his little ducks’ head, he told them a story.

“Prince Remmarguts lives in his kingdom UDF – United Delta of Freedom. One day their neighboring country sent them Princess Uyuw on a diplomatic mission.”

“Erenow, the princess sent Remmarguts a letter, informing him that she would come to the hall and hold commercial talks with UDF if and only if the prince go and meet her via the K-th shortest path. (in fact, Uyuw does not want to come at all)”

Being interested in the trade development and such a lovely girl, Prince Remmarguts really became enamored. He needs you - the prime minister’s help!

DETAILS: UDF’s capital consists of N stations. The hall is numbered S, while the station numbered T denotes prince’ current place. M muddy directed sideways connect some of the stations. Remmarguts’ path to welcome the princess might include the same station twice or more than twice, even it is the station with number S or T. Different paths with same length will be considered disparate.

Input

The first line contains two integer numbers N and M (1 <= N <= 1000, 0 <= M <= 100000). Stations are numbered from 1 to N. Each of the following M lines contains three integer numbers A, B and T (1 <= A, B <= N, 1 <= T <= 100). It shows that there is a directed sideway from A-th station to B-th station with time T.
The last line consists of three integer numbers S, T and K (1 <= S, T <= N, 1 <= K <= 1000).

Output

A single line consisting of a single integer number: the length (time required) to welcome Princess Uyuw using the K-th shortest path. If K-th shortest path does not exist, you should output “-1” (without quotes) instead.

Sample Input

2 2
1 2 5
2 1 4
1 2 2

Sample Output

14

---

在这道题目中，要求很明确，就是需要你求从s到t的第K短路

第k短路：

K短路的定义：假设从1出发，有M条长度不同的路径可以到达点N，则K短路就是这M条路径中第K小的路径长度。
以上所述，设 f(n) 为 n 节点的过估价函数，则 f(n) = g(n) + h(n); h(n) 就是我们所说的‘启发式函数’，表示为终点 t 到节点 n 的最佳路径代价，g（n）表示 g 当前从 s 到 节点 n 所走的实际路径的长度，即最终结果。
即

估价函数=当前值+当前位置到终点的距离

Solution：

(1)将有向图的所有边反向,以原终点t为源点,求解t到所有点的最短距离，即 h(n);
(2)新建一个优先队列,将源点s加入到队列中，队列中维护的是估价函数的值;
(3)从优先级队列中弹出 f(p) 最小的点 p,如果点 p 就是 t,则计算t出队的次数;
如果当前为 t 的第 k 次出队,则当前路径的长度就是 s 到 t 的第 k 短路的长度,算法结束;
否则遍历与 p 相连的所有的边,将扩展出的到p的邻接点信息加入到优先级队列;

Code：

#include
#include
#include
#include
#include
#include
#include

using namespace std;

struct node{
	int v;//表示顶点编号
	int w;//表示 v 顶点到源点的距离最小值 
	node(){}
	node(int v, int w) : v(v), w(w){}
	bool operator < (const node& e) const {
		return w < e.w;
	}
};

struct Edge{
	int u;
	int v;
	int w;
	int next;
	Edge(){}
	Edge(int u, int v, int w, int next) : u(u), v(v), w(w), next(next){}
}; 

struct node2{
	int v;//表示顶点的编号
	int g;//每个顶点的 f(n)，表示源点到任意点的距离 
	int f;//f(n) = g(n) + h(n) 
	node2(){}
	node2(int v, int g, int f) : v(v), g(g), f(f){}
	bool operator < (const node2 &x) const{
		if(x.f == f)
			return x.g < g;
		return x.f < f; 
	}
};

const int maxn = 1005;
const int maxm = 100005; 
const int inf = 0x3f3f3f3f;
int N,M,S,E,K,T,first[maxm],first2[maxm],cnt,cnt2;
node dis[maxn];
Edge edge[maxm<<2]; 
Edge edge2[maxm<<2];
bool vis[maxn];

void init()
{
	cnt = cnt2 = 1;//计数-边的编号
	memset(first, -1, sizeof(first));
	memset(first2, -1, sizeof(first2));
	for(int i = 1; i <= N; i++)
	{
		dis[i].w = inf;
		dis[i].v = i;
		vis[i] = false;
	} 
}

void addEdge(int u, int v, int w)
{
	edge[cnt] = Edge(u, v, w, first[u]);//记录某个顶点所访问到的 "前一条边" 的编号
	first[u] = cnt;//不断的覆盖某个顶点所访问到的 "当前的边" 的编号
	cnt++;
}

void addEdge2(int u, int v, int w)
{
	edge2[cnt2] = Edge(u, v, w, first2[u]);
	first2[u] = cnt2;
	cnt2++;
}
 
void dijstra(int s)//求出 h(n)--任意点到终点 E 的距离 
{
	dis[s].w = 0;
	priority_queue pq; 
	pq.push(dis[s]);
	while(!pq.empty())
	{
		node now = pq.top();
		pq.pop();
		int from = now.v;
		int cost = now.w;
//		if(vis[from])	continue;
//		vis[from] =  true;
		for(int i = first[from]; i != -1; i = edge[i].next)
		{
			int to = edge[i].v;
			if(dis[to].w > edge[i].w + cost)
			{
				dis[to].w = edge[i].w + cost;
				pq.push(dis[to]);
			}
		}
	}
}

int A_star(int s, int t)
{
	if(s == t)//始点和终点一样，必须绕一圈回来 
		K++;
	if(dis[s].w == inf)//始点和终点不可达 
		return -1;
	int num = 0;
	priority_queue pq;//队列中维护的为f(n)-估价函数的值 
	pq.push(node2(s, 0, dis[s].w));
	while(!pq.empty())
	{
		node2 e = pq.top();
//		cout<>N>>M;
 	init();
 	for(int i = 0; i < M; i++)
 	{
 		cin>>from>>to>>w;	
 		addEdge(to, from, w);//将边反向，求出 h(n)--任意点到终点 E 的距离为 dis[] 
 		addEdge2(from, to, w);
	}
	cin>>S>>E>>K;
	dijstra(E);
	int ans = A_star(S, E);
	printf("%d\n",ans); 
	return 0;
}

--------------------- 本文来自 Z_Mendez 的CSDN 博客 ，全文地址请点击：https://blog.csdn.net/z_mendez/article/details/47057461?utm_source=copy