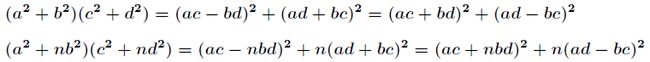骚猪队的模板

SaoZhu Team Code Library 2017.11

TAGS: ACM

for newest edition, click here

East China Normal University

Chen WeiWen - Software Engineering

Cao ZhiJie - Computer Science

Zhu XuLiang - Mathematics

常用STL

map的Upperbound

map::iterator se = mp.upper_bound(mid);
返回迭代器

优先队列

priority_queueQ;//采用默认优先级构造队列
priority_queue,cmp1>que1;//最小值优先  
priority_queue,cmp2>que2;//最大值优先  

Q.push(x);
int x = Q.top(); Q.pop();

multiset

begin()        返回指向第一个元素的迭代器
clear()        清除所有元素
count()        返回某个值元素的个数
empty()        如果集合为空，返回 true
end()          返回指向最后一个元素的迭代器
erase()        删除集合中的元素 ( 参数是一个元素值，或者迭代器)
find()         返回一个指向被查找到元素的迭代器
insert()       在集合中插入元素
size()         集合中元素的数目
lower_bound()  返回指向大于（或等于）某值的第一个元素的迭代器
upper_bound()  返回大于某个值元素的迭代器
equal_range()  返回集合中与给定值相等的上下限的两个迭代器

multiset  po;
multiset ::iterator L, R, it;

离散化lower_lound

lower_bound 第一个出现的值大于等于val的位置

upper_bound 最后一个大于等于val的位置，也是有一个新元素val进来时的插入位置

sort(a + 1, a + A+1);
A = unique(a + 1, a + A+1) - (a + 1);
for (int i = 1; i <= n; i++){ // segtree
    int L = lower_bound(a+1, a+A+1, l[i]) - a;
    int R = lower_bound(a+1, a+A+1, r[i]) - a;
    T.update(L, R, i, 1, T.M+1,1);
}
------------use in ChairTree-------------------
for (int i = 1; i <= n; i++) {
    scanf("%d", &arr[i]);
    Rank[i] = arr[i];
}
sort(Rank + 1, Rank + n+1);//Rank存储原值
int m = unique(Rank + 1, Rank + n +1) - (Rank + 1);//这个m很重要，WA一天系列
for (int i = 1; i <= n; i++) {//离散化后的数组，仅仅用来更新
    arr[i] = lower_bound(Rank + 1, Rank + m+1, arr[i]) - Rank;
}
==================CZJ排序去重===================
sort(vecs.begin(), vecs.end());
vecs.resize(unique(vecs.begin(), vecs.end()) - vecs.begin());

vector 的插入删除

// erase the 6th element
myvector.erase (myvector.begin()+5);

// erase the first 3 elements:
myvector.erase (myvector.begin(),myvector.begin()+3);

// ------------inserting into a vector-----------
#include 
#include 

int main (){
  std::vector myvector (3,100);
  std::vector::iterator it;

  it = myvector.begin();
  it = myvector.insert ( it , 200 );

  myvector.insert (it,2,300);

  // "it" no longer valid, get a new one:
  it = myvector.begin();

  std::vector anothervector (2,400);
  myvector.insert (it+2,anothervector.begin(),anothervector.end());

  int myarray [] = { 501,502,503 };
  myvector.insert (myvector.begin(), myarray, myarray+3);

  std::cout << "myvector contains:";
  for (it=myvector.begin(); it

bitset

构造函数
bitset b;
b有n位，每位都为0.参数n可以为一个表达式.
如bitset<5> b0;则"b0"为"00000";

bitset b(unsigned long u);
b有n位,并用u赋值;如果u超过n位,则顶端被截除
如:bitset<5>b0(5);则"b0"为"00101";

bitset b(string s);
b是string对象s中含有的位串的副本
string bitval ( "10011" );
bitset<5> b0 ( bitval4 );
则"b0"为"10011";

bitset b(s, pos);
b是s中从位置pos开始位的副本,前面的多余位自动填充0;
string bitval ("01011010");
bitset<10> b0 ( bitval5, 3 );
则"b0" 为 "0000011010";

bitset b(s, pos, num);
b是s中从位置pos开始的num个位的副本,如果num b0 ( bitval5, 3, 6 );
则"b0" 为 "100110";

bool any()      是否存在置为1的二进制位？和none()相反
bool none()     是否不存在置为1的二进制位,即全部为0？和any()相反.
size_t count()  二进制位为1的个数.
size_t size()   二进制位的个数
flip()          把所有二进制位逐位取反
flip(size_t pos)把在pos处的二进制位取反
bool operator[]( size_type _Pos )获取在pos处的二进制位
set()           把所有二进制位都置为1
set(pos)        把在pos处的二进制位置为1
reset()         把所有二进制位都置为0
reset(pos)      把在pos处的二进制位置为0
test(size_t pos)在pos处的二进制位是否为1？
unsigned long to_ulong( )用同样的二进制位返回一个unsigned long值
string to_string ()返回对应的字符串.

STL补充

Stringstream的使用：

　　string str;  
　　stringstream ss;  
　　while(getline(cin,str)){ //getline函数的返回值是其中的流cin。一旦cin读取错误就是false。  
　　　　ss<> a) sum+=a;     //当流里没有东西的时候，退出循环。  
　　　　cout<

STL补充
lower_bound: 返回一个ForwardIterator，指向在有序序列范围内的可以插入指定值而不破坏容器顺序的第一个位置。重载函数使用自定义比较操作。

upper_bound: 返回一个ForwardIterator，指向在有序序列范围内插入value而不破坏容器顺序的最后一个位置，该位置标志一个大于value的值。重载函数使用自定义比较操作。

inplace_merge: 合并两个有序序列，结果序列覆盖两端范围。重载版本使用输入的操作进行排序。

merge: 合并两个有序序列，存放到另一个序列。重载版本使用自定义的比较。

nth_element: 将范围内的序列重新排序，使所有小于第n个元素的元素都出现在它前面，而大于它的都出现在后面。重载版本使用自定义的比较操作。

sort: 以升序重新排列指定范围内的元素。重载版本使用自定义的比较操作。

stable_sort: 与sort类似，不过保留相等元素之间的顺序关系。

unique: 清除序列中重复元素，和remove类似，它也不能真正删除元素。重载版本使用自定义比较操作。

next_permutation: 取出当前范围内的排列，并重新排序为下一个字典序排列。重载版本使用自定义的比较操作。

prev_permutation: 取出指定范围内的序列并将它重新排序为上一个字典序排列。如果不存在上一个序列则返回false。重载版本使用自定义的比较操作。

scanf 用法及陷阱

格式字符 说明
%c 读入一个字符
%d 读入十进制整数
%i 读入十进制，八进制，十六进制整数
%o 读入八进制整数
%x 读入十六进制整数
%X 同上
%c 读入一个字符
%s 读入一个字符串
%f 读入一个浮点数
%p 读入一个指针
%u 读入一个无符号十进制整数

scanf一个double数据，是%lf，printf一个float或者double都是%f

大写L,加f输出long double。最后的f小写和大写没影响，但是第一个 l 必须大写成L。

unsigned long long %llu

printf 对齐方式

1.默认左对齐

2.在打印数字宽度前面加一个-,左对齐%-10d

3.在数字宽度前面不加-,右对齐%10d

rope

丧心病狂的可持久化平衡树

1）头文件 #include
2)调用命名空间 using namespace __gnu_cxx;

rope适用于大量、冗长的串操作，而不适合单个字符操作

rope本质是封装好的类似块状链表的东东，有人说是logn的，但也有说是n^0.5的。rope不支持一切数值操作，如第k大

先介绍几个可能使用到的函数

1）append()

string &append(const string &s,int pos,int n); // 把字符串s中从pos开始的n个字符连接到当前字符串的结尾

或

a.append(b);

2）substr()

s.substr(0,5); // 获得字符串s中从第零位开始长度为5的字符串（默认时长度为刚好开始位置到结尾）

定义/声明

rope str;
r="abcdefg"

具体内容
总的来说，

1）运算符：rope支持operator += -= + - < ==
2）输入输出：可以用<<运算符由输入输出流读入或输出。
3）长度/大小：调用length()，size()都可以哦
4）插入/添加等：
push_back(x);  // 在末尾添加x
insert(pos,x);  // 在pos插入x，自然支持整个char数组的一次插入
erase(pos,x);  // 从pos开始删除x个
copy(pos,len,x);  // 从pos开始到pos+len为止用x代替
replace(pos,x);  // 从pos开始换成x
substr(pos,x);  // 提取pos开始x个
at(x)/[x];  // 访问第x个元素

访问

1）迭代器：不说，在竞赛是超时大忌

2）单点访问，直接用数组形式调用下标即可

应用

一、bzoj1269 文本编辑器

实现操作：
1.（已知）move k：移动光标到目标，初始为0
2.（已知）prev：光标前移一个字符
3.（已知）next：光标后移一个字符
4.insert n s：在光标后插入长度为n的字符串s光标位置不变
5.delete n 删除光标后的n个字符，光标位置不变
6.rotate n 反转光标后的n个字符，光标位置不变
7.get 输出光标后一个字符，光标位置不变

solution

为实现反转操作且保证不超时，我们不调用rope自带的可怕函数，暴力构建两个rope，插入时一个正序插入一个倒序插入，区间即为子串赋值

#include
#include
#include
using namespace std;
using namespace __gnu_cxx;
inline int Rin(){
  int x=0,c=getchar(),f=1;
  for(;c<48||c>57;c=getchar())
    if(!(c^45))f=-1;
  for(;c>47&&c<58;c=getchar())
    x=(x<<1)+(x<<3)+c-48;
  return x*f;
}
int n,pos,x,l;
ropea,b,tmp;
char sign[10],ch[1<<22],rch[1<<22];
int main(){
  n=Rin();
  while(n--){
    scanf("%s",sign);
    switch(sign[0]){
    case'M':pos=Rin();break;
    case'P':pos--;break;
    case'N':pos++;break;
    case'G':putchar(a[pos]);putchar('\n');break;
    case'I':
      x=Rin();
      l=a.length();
      for(int i=0;i

线性代数

矩阵快速幂

#include
#include
#include
using namespace std;
typedef long long LL;
const LL MOD = 1000000007LL;
LL n,m;

struct matrix{
    static const int MATRIX_N = 11;
    LL a[MATRIX_N][MATRIX_N];
    int row, col;
    matrix():row(MATRIX_N),col(MATRIX_N){memset(a,0,sizeof(a));}
    matrix(int x, int y):row(x),col(y){memset(a,0,sizeof(a));}
    LL* operator [] (int x){return a[x];}

    matrix operator * (matrix x){
        matrix tmp(row, x.col);
        for(int i = 0; i < row; i++)
            for(int j = 0; j < col; j++) if(a[i][j])//稀疏矩阵优化
                for(int k = 0; k < x.col; k++) if (x[j][k]){
                    tmp[i][k] += a[i][j] * x[j][k];
                    //mult(a[i][j], x[j][k], MOD);
                    tmp[i][k] %= MOD;
                }
        return tmp;
    }
    void operator *= (matrix x){*this = *this * x;}

    matrix operator ^ (LL x){
        matrix ret(row, col);
        for (int i = 0; i < col; i++) ret[i][i] = 1;
        matrix tmp = *this;
        for (; x; x >>= 1, tmp *= tmp){if (x&1) ret *= tmp;}
        return ret;
    }

    void print(){
        for (int i = 0; i < row; i++){
            for (int j = 0; j < col; j++) printf("%lld ",a[i][j]);
            puts("");
        }
    }
};

int main() {
    LL n;
    matrix B(3, 1);
    while(scanf("%lld%lld%lld%lld", &B[0][0], &B[1][0], &B[2][0], &n) == 4) {
        matrix A(3, 3);
        A[0][0] = 0; A[0][1] = 1; A[0][2] = 0;
        A[1][0] = 0; A[1][1] = 0; A[1][2] = 1;
        A[2][0] = 0; A[2][1] = 1; A[2][2] = 1;
        A = A ^ n;
        matrix C(3, 1);
        C = A * B;
        printf("%lld\n", (C[0][0] + C[1][0] + C[2][0]) % MOD);
    }
    return 0;
}

就是快速幂(czj)

//快速乘法
LL fast_multi(LL m, LL n, LL mod){
    LL ans = 0;//注意初始化是0，不是1 
    n = (n % mod + mod) % mod;
    for (;n; n >>= 1){
        if (n & 1) ans = (ans + m) % mod;
        m = (m + m) % mod;//和快速幂一样，只不过这里是加 
    }
    return ans % mod;
}
LL fast_pow(LL a, LL n, LL mod){//快速幂 
    LL ans = 1;
    for (;n;n >>= 1){
        if (n & 1) ans = fast_multi(ans, a, mod) % mod;//不能直接乘 
        a = fast_multi(a, a, mod) % mod;
    }
    return ans;
}

线性递推函数杜教模板(快速幂下岗了)

#include 
#include 
#include 
#include 
#include 
#include 

高斯消元（naive）

判断是否有解

求解见红书

int Gauss(matrix a, int m, int n){
    int x_cnt = 0;
    int col, k;         //col为列号,k为行号
    for (k=0,col=0;k

bitset优化XOR方程组

//HDU 5833 XOR GUASS bitset, 白书P160

#include 
using namespace std;
const int maxn = 2005;
const int mod = 1e9+7;
int n, vis[maxn], prime[maxn], cnt;
void pre_deal(){
    for(int i = 2; i < maxn; i++){
        if (vis[i]) continue;
        prime[cnt++] = i;
        for(int j = i; j < maxn; j += i) vis[j] = 1;
    }
}
bitset <330> A[305]; //A[i][j]就表示第j个数的这个i素数是奇数还是偶数

int main(){
    pre_deal();
    int T, ks = 0; scanf("%d", &T);
    while(T--){
        printf("Case #%d:\n", ++ks);
        for(int i = 0; i < 305; i++) A[i].reset();
        scanf("%d", &n);
        for(int i = 0; i < n; i++){
            long long x;
            scanf("%lld", &x);
            for(int j = 0; j < cnt; j++){
                if(x%prime[j] == 0){
                    int flag = 0;
                    while(x%prime[j] == 0){
                        x /= prime[j];
                        flag ^= 1;
                    }
                    A[j][i] = flag;
                }
            }
        }
        int i = 0, j = 0; //xor消元之后j就是秩
        for(i = 0; i < n; i++){
            int id = -1;
            for(int k = j; k < cnt; k++){
                if(A[k][i]){id = k; break;}
            }
            if(id == -1) continue;
            swap(A[j], A[id]);
            for(int k = j + 1; k < cnt; k++)
                if(A[k][i]) A[k] ^= A[j];
            j++;
        }
        int ans = 1;
        for(int i = 0; i < n - j; i++) ans = ans * 2 % mod;
        ans--;
        printf("%d\n", ans);
    }
    return 0;
}

16行FFT

模板题：多项式乘法

#include
using namespace std;

const double PI = acos (-1.);
const int N = 1 << 22;
std::complex  AA[N], BB[N];

void fft (std::complex  a[], int n, int f) {
	for (int i = 0, j = 0; i < n; ++i) {
		if (i > j) std::swap (a[i], a[j]);
		for (int t = n >> 1; (j ^= t) < t; t >>= 1);
	}
	static std::complex  w[N];
	for (int i = 0; i <= n; ++i)
		w[i] = std::complex  (cos (2 * PI * i / n), sin (2 * PI * i / n));
	for (int i = 2; i <= n; i <<= 1)
		for (int j = 0; j < n; j += i)
			for (int k = 0; k < (i >> 1); ++k) {
				std::complex  A = a[j + k];
				std::complex  B = w[f ? n - n / i * k : n / i * k] * a[j + k + (i >> 1)];
				a[j + k] = A + B; a[j + k + (i >> 1)] = A - B;

			}
	if (f) for (int i = 0; i < n; ++i) a[i] = std::complex  (a[i].real () / n, a[i].imag ());
}

int main(){
    int A, B;
    std::cin >> A >> B;
    for (int i = 0; i <= A; ++i) {
        int u; std::cin >> u;
        AA[i] = std::complex  (u, 0);
    }
    for (int i = 0; i <= B; ++i) {
        int u; std::cin >> u;
        BB[i] = std::complex  (u, 0);
    }
	int n = 1;
	while (n <= A + B + 1) n *= 2;
    fft (AA, n, 0);
    fft (BB, n, 0);
    for (int i = 0; i < n; ++i) AA[i] = AA[i] * BB[i];
    fft (AA, n, 1);
    for (int i = 0; i <= A + B; ++i) std::cout << (int) round (AA[i].real ()) << " \n"[i == A + B];
    return 0;
}

NTT（对任意数取模）

// 多项式乘法 系数对MOD=1000000007取模， 常数巨大，慎用  
// 只要选的K个素数乘积大于MOD*MOD*N,理论上MOD可以任取。  
#define MOD 1000000007  
#define K 3  
const int m[K] = {1004535809, 998244353, 104857601};  
#define G 3  

int qpow(int x, int k, int P) {  
    int ret = 1;  
    while(k) {  
        if(k & 1) ret = 1LL * ret * x % P;  
        k >>= 1;  
        x = 1LL * x * x % P;  
    }  
    return ret;  
}  
  
struct _NTT {  
    int wn[25], P;  

    void init(int _P) {  
        P = _P;  
        for(int i = 1; i <= 21; ++i) {        
            int t = 1 << i;        
            wn[i] = qpow(G, (P - 1) / t, P);        
        }  
    } 
    void change(int *y, int len) {  
        for(int i = 1, j = len / 2; i < len - 1; ++i) {        
            if(i < j) swap(y[i], y[j]);        
            int k = len / 2;        
            while(j >= k) {        
                j -= k;        
                k /= 2;        
            }        
            j += k;        
        }   
    }  
    void NTT(int *y, int len, int on) {  
        change(y, len);        
        int id = 0;        
        
        for(int h = 2; h <= len; h <<= 1) {        
            ++id;        
            for(int j = 0; j < len; j += h) {        
                int w = 1;        
                for(int k = j; k < j + h / 2; ++k) {        
                    int u = y[k];        
                    int t = 1LL * y[k+h/2] * w % P;       
                    y[k] = u + t;        
                    if(y[k] >= P) y[k] -= P;        
                    y[k+h/2] = u - t + P;        
                    if(y[k+h/2] >= P) y[k+h/2] -= P;    
                    w = 1LL * w * wn[id] % P;  
                }        
            }        
        }        
        if(on == -1) {        
            for(int i = 1; i < len / 2; ++i) swap(y[i], y[len-i]);        
            int inv = qpow(len, P - 2, P);        
            for(int i = 0; i < len; ++i)     
                y[i] = 1LL * y[i] * inv % P;  
        }        
    }  
    void mul(int A[], int B[], int len) {  
        NTT(A, len, 1);  
        NTT(B, len, 1);  
        for(int i = 0; i < len; ++i) A[i] = 1LL * A[i] * B[i] % P;  
        NTT(A, len, -1);  
    }  
}ntt[K];  
  
int tmp[N][K], t1[N], t2[N];  
int r[K][K];  
  
int CRT(int a[]) {  
    int x[K];  
    for(int i = 0; i < K; ++i) {  
        x[i] = a[i];  
        for(int j = 0; j < i; ++j) {  
            int t = (x[i] - x[j]) % m[i];  
            if(t < 0) t += m[i];  
            x[i] = 1LL * t * r[j][i] % m[i];  
        }  
    }  
    int mul = 1, ret = x[0] % MOD;  
    for(int i = 1; i < K; ++i) {  
        mul = 1LL * mul * m[i-1] % MOD;  
        ret += 1LL * x[i] * mul % MOD;  
        if(ret >= MOD) ret -= MOD;  
    }  
    return ret;  
}  
  
void mul(int A[], int B[], int len) {  
    for(int id = 0; id < K; ++id) {
        for(int i = 0; i < len; ++i) {  
            t1[i] = A[i];
            t2[i] = B[i];
        }  
        ntt[id].mul(t1, t2, len);  
        for(int i = 0; i < len; ++i) tmp[i][id] = t1[i];  
    }  
    for(int i = 0; i < len; ++i){
        A[i] = CRT(tmp[i]);
  
    }  
}  
  
void init() {  
    for(int i = 0; i < K; ++i) {
        for(int j = 0; j < i; ++j) {
            r[j][i] = qpow(m[j], m[i] - 2, m[i]);  
        }
    }
    for(int i = 0; i < K; ++i) ntt[i].init(m[i]);
}

单纯形法

#include
using namespace std;
const int INF=0x3f3f3f3f;
const double EPS=1e-9;
int n,m;
/*
求解的为标准形式
max z=CX
满足    AX<=B
        X>=0
约定 B>=0

对于形式为
min z=CX
满足    AX >= B
        X>=0
约定B>=0
可以转换为对偶形式
max w=(B^T)Y
满足    (A^T)Y<=(C^T)
        Y>=0
hint:^T表示矩阵翻转
*/

namespace Linear_Programming{
double A[10100][1010],b[10100],c[1010],v;
void Pivot(int l,int e){
    int i,j;
    b[l] /= A[l][e];
    for (i = 1; i <= n; i++) if (i != e) 
        A[l][i] /= A[l][e];
    A[l][e] = 1 / A[l][e];

    for(i=1; i<=m; i++)
        if(i != l && fabs(A[i][e]) > EPS){
            b[i] -= A[i][e] * b[l];
            for(j = 1; j <= n; j++) if (j != e)
                A[i][j] -= A[i][e] * A[l][j];
            A[i][e] = -A[i][e] * A[l][e];
        }
        
    v += c[e]*b[l];
    for(i=1; i<=n; i++) if(i!=e)
        c[i]-=c[e]*A[l][i];
    c[e] = -c[e] * A[l][e];
}
double Simplex(){
    int i,l,e;
    while(1){
        for(i=1; i<=n; i++) if(c[i]>EPS) break;
        if((e=i) == n+1) return v;
        double temp = INF;
        for(i = 1; i <= m; i++)
            if( A[i][e]>EPS && b[i]/A[i][e]

组合数学

常用公式和找规律

斯特林公式
n! 约等于 sqrt(2*pi*n)*pow(1.0*n/e,n)

带标号连通图计数
1 1 1 4 38 728 26704 1866256 251548592
h(n)=2^(n(n-1)/2)
f(n) = h(n)-sum{C(n-1,k-1)*f(k)*h(n-k)}(k=1...n-1)

不带标号n个节点的有根树计数
1, 1, 2, 4, 9, 20, 48, 115, 286, 719, 1842,

不带标号n个节点的树的计数
1,2,3,6,11,23,47,106,235
OEIS
A(x) = 1 + T(x) - T^2(x)/2 + T(x^2)/2, where T(x) = x + x^2 + 2*x^3 + ... is the g.f. for A000081

错排公式
D[1] = 0; D[2] = 1;
for(int i = 3; i < 25; i++) {
    D[i] = (i - 1) * (D[i - 1] + D[i - 2]);
}

卡特兰数
1 2 5 14 42 132 429 1430 4862 16796
binomial(2*n, n)-binomial(2*n, n-1)
Sum_{k=0..n-1} a(k)a(n-1-k)


Stirling数，又称为斯特灵数。
　　在组合数学，Stirling数可指两类数，都是由18世纪数学家James Stirling提出的。
　　第一类Stirling数是有正负的，其绝对值是包含n个元素的集合分作k个环排列的方法数目。
　　第二类Stirling数是把包含n个元素的集合划分为正好k个非空子集的方法的数目。
递推公式
　　第一类Stirling数是有正负的，其绝对值是包含n个元素的集合分作k个环排列的方法数目。
　　递推公式为，
　　S(n,0) = 0, S(1,1) = 1.
　　S(n 1,k) = S(n,k-1) nS(n,k)。
　　第二类Stirling数是把包含n个元素的集合划分为正好k个非空子集的方法的数目。
　　递推公式为：
　　S(n,k)=0; (n

详解ACM组合数处理，

O(n2)算法——杨辉三角

O(n)算法——阶乘取模 + 乘法逆元

C(m,n) = n! / m! / (n - m)!

如果p是质数，直接quick_mod(b, p-2) % p 费马小定理求逆元

LL C(LL n, LL m){
    if(m > n) return 0;  
    LL ans = 1; 
    for(int i = 1; i <= m; i++){
        LL a = (n + i - m) % MOD;  
        LL b = i % MOD;  
        ans = ans * (a * quick_mod(b, p-2) % MOD) % MOD;  
    }  
    return ans;  
}  

如果n,m很大 达到1e18，但是p很小 <= 1e5 ，我们可以利用这个p

Lucas定理：C(n, m) % p = C(n / p, m / p) * C(n%p, m%p) % p

LL Lucas(LL n, LL m){
    if(m == 0) return 1;  
    return C(n % p, m % p) * Lucas(n / p, m / p) % p;  
}
void InitFac(){//阶乘预处理
    fac[0]  = 1;  
    for(int i=1; i<=n; i++)  
        fac[i] = (fac[i-1] * i) % MOD;  
}
LL C(LL n,LL m,LL p,LL fac[]){
    if(n < m) return 0;  
    return fac[n] * quick_mod(fac[m] * fac[n-m], p - 2, p) % p;  
}

组合数奇偶性结论：

如果（n&m) == m 那么c(m,n)是奇数，否则是偶数

生成函数 五边形数定理 整数拆分模板

hdu4658

问一个数n能被拆分成多少种方法，且每一种方法里数字重复个数不能超过k（等于k）。

$F(n,k)=p(n)-{\sum }_{i=1}^{\infty }(-1{)}^i[p(n-\frac{(3i-1)i}{2}+p\frac{(3i+1)i}{2}]$

f[n]=∑(-1)^(k-1)*(f[n-k*(3*k-1)/2]+f[n-k*(3*k+1)/2])

#include   
#include   
#include   
using namespace std;  
const int N = 100005;  
const int MOD = 1000000007;  
int dp[N];  
  
void Init()  {  
    dp[0] = 1;  
    for(int i=1;i i) break;  
            int tt = dp[i-t];  
            if(t+j <= i) tt = (tt + dp[i-t-j])%MOD;  
            if(j&1) dp[i] = (dp[i] + tt)%MOD;  
            else    dp[i] = (dp[i] - tt + MOD)%MOD;  
        }  
    }  
}  
  
int Work(int n,int k) {  
    int ans = dp[n];  
    for(int i=1;;i++){  
        int t = k*i*(3*i-1) / 2;  
        if(t > n) break;  
        int tt = dp[n-t];  
        if(t + i*k <= n) tt = (tt + dp[n-t-i*k])%MOD;  
        if(i&1) ans = (ans - tt + MOD)%MOD;  
        else    ans = (ans + tt)%MOD;  
    }  
    return ans;  
}  
  
int main(){  
    Init();  
    int n,k,t;  
    scanf("%d",&t);  
    while(t--){  
        scanf("%d%d",&n,&k);  
        printf("%d\n",Work(n,k));  
    }  
    return 0;  
}  

容斥原理dfs

题意找与n,m互质的第k个数
思路：二分
找到最小的x，使得小于或等于x的数中满足条件的数的个数大于或等于k
预处理n,m的质因数表
k是深度，也就是当前质因数位置
t是奇偶判断
s是质数乘积
n是传进去的x

void dfs(LL k,LL t,LL s,LL n)  {  
    if(k==num)  {  
        if(t&1) ans-=n/s;  
        else    ans+=n/s;  
        return;  
    }  
    dfs(k+1,t,s,n);  
    dfs(k+1,t+1,s*fac[k],n);  //fac[k]是质因数表
}

//二分调用
dfs(0,0,1,mid);

求（1，b）区间和（1，d）区间里面gcd(x, y) = k的数的对数（1<=x<=b , 1<= y <= d）。
b和d分别除以k之后的区间里面，只需要求gcd(x, y) = 1就可以了，这样子求出的数的对数不变。
这道题目还要求1-3 和 3-1 这种情况算成一种，因此只需要限制$x<y$就可以了

只需要枚举x，然后确定另一个区间里面有多少个y就可以了。因此问题转化成为区间（1， d）里面与x互素的数的个数
先求出x的所有质因数，因此$(1，d)$区间里面是x的质因数倍数的数都不会与x互素，因此，只需要求出这些数的个数，减掉就可以了。
如果w是x的素因子，则（1，d）中是w倍数的数共有d/w个。

容斥原理：
所有不与x互素的数的个数= 1个因子倍数的个数 - 2个因子乘积的倍数的个数 + 3个……-……

答案很大，用long long。
所有数的素因子，预先处理保存一下，不然会超时的。

#include   
#include   
#include   
#include   
using namespace std;  
#define N 100005  
typedef long long ll;  
vector x[N];  
bool is[N];  
  
void prime() {  
    memset(is, false, sizeof(is));  
    for (int i=0; i d) { a = b; b = d; d = a; }  
        long long ans = 0;  
        for (int i=1; i<=d; i++) {  
            k = min(i, b);  
            ans += k;  
            for (int j=1; j<(1<

村民排队问题模型

一堆数，其中有一些两两关系，（A,B）表示A在B前面，求排列数

// UVa11174 Stand in a Line
// Rujia Liu

int mul_mod(int a, int b, int n) {
  a %= n; b %= n;
  return (int)((long long)a * b % n);
}

void gcd(int a, int b, int& d, int& x, int& y) {
  if(!b){ d = a; x = 1; y = 0; }
  else{ gcd(b, a%b, d, y, x); y -= x*(a/b); }
}

int inv(int a, int n) {
  int d, x, y;
  gcd(a, n, d, x, y);
  return d == 1 ? (x%n+n)%n : -1;
}

#include
#include
#include
using namespace std;

const int maxn = 40000 + 10;
const int MOD = 1000000007;

vector sons[maxn];
int fa[maxn], fac[maxn], ifac[maxn];

int mul_mod(int a, int b) {
  return mul_mod(a, b, MOD);
}

// fac[i] = (i!)%MOD, ifac[i]为fac[i]在模MOD下的逆
void preprocess() {
  fac[0] = ifac[0] = 1;
  for(int i = 1; i < maxn; i++) {
    fac[i] = mul_mod(fac[i-1], i);
    ifac[i] = inv(fac[i], MOD);
  }
}

// 组合数C(n,m)除以MOD的余数
int C(int n, int m) {
  return mul_mod(mul_mod(fac[n], ifac[m]), ifac[n-m]);
}

// 统计以u为根的子树有多少种排列。size为该子树的结点总数
int count(int u, int& size) {
  int d = sons[u].size();
  vector sonsize; // 各子树的大小
  size = 1;
  int ans = 1;
  for(int i = 0; i < d; i++) {
    int sz;
    ans = mul_mod(ans, count(sons[u][i], sz));
    size += sz;
    sonsize.push_back(sz);
  }
  int sz = size-1; // 非根结点的个数
  for(int i = 0; i < d; i++) {
    ans = mul_mod(ans, C(sz, sonsize[i]));
    sz -= sonsize[i];
  }
  return ans;
}

int main() {
  int T;
  scanf("%d", &T);
  preprocess();  
  while(T--) {
    int n, m;
    scanf("%d%d", &n, &m);
    memset(fa, 0, sizeof(fa));
    for(int i = 0; i <= n; i++) sons[i].clear();
    for(int i = 0; i < m; i++) {
      int a, b;
      scanf("%d%d", &a, &b);
      fa[a] = b;
      sons[b].push_back(a);
    }
    // 没有父亲的结点称为虚拟结点的儿子
    for(int i = 1; i <= n; i++)
      if(!fa[i]) sons[0].push_back(i);
    int size;
    printf("%d\n", count(0, size));
  }
  return 0;
}

SG函数，博弈

/**********************
每组数据都改变策略
**********************/
#include
#include
#include
#include
#include
#include
using namespace std;
typedef int LL;
const int MAXN = 1e4 + 5;
const int MAXM = 1e4;
int sg[MAXN];
bool Hash[MAXN];
int f[MAXN];
int N;
void getsg(int n){
    memset(sg,0,sizeof sg);
    for (int i=1;i<=MAXM;i++){
        memset(Hash,false,sizeof Hash);
        for(int j = 0; j < N && i >= f[j]; j++) {
            Hash[sg[i-f[j]]] = true;
			/****************上海大学校赛教训，板不要理解错。
				这不是一堆拆两堆，这是每个可以转移的状态都标记。
			****************/
        }
        for (int j=0;j<=MAXM;j++){
            if (!Hash[j]){
                sg[i]=j; break;
            }
        }
        //cout << i << " " << sg[i] << endl;
    }
}
int main() {
    //freopen("out.txt", "w", stdout);
    while(cin >> N, N) {
        for(int i = 0; i < N; i++) {
            scanf("%d", f + i);
        }
        sort(f, f + N);//一定要排序
        getsg(MAXM);
        int m;
        cin >> m;
        for(int i = 0; i < m; i++) {
            int n;
            cin >> n;
            int ans = 0;
            for(int i = 0; i < n; i++) {
                int x;
                scanf("%d", &x);
                ans ^= sg[x];
            }
            printf("%s", ans ? "W" : "L");
        }
        printf("\n");
    }
    return 0;
}

/***************
独立的棋盘横向移动，看成一个子向另一个子一直在减小，NIM两子间距
***************/

/***********************
有一个操作可以把一堆拆成两堆，枚举拆分点
***********************/
for(int j = 0; j <= i - x; j++) {
	Hash[sg[j] ^ sg[i - x - j]] = 1;
}

/***********************
拿走最后一个的人输，需要特判全是1的情况。
全是1，分奇偶。不全是1，同直接NIM
***********************/

/********************
两维的一样拆分成两个异或。SG[][]两维
0行，0列特殊处理。直接设置成离原点的距离。
2 2
.#
..
2 2
.#
.#
0 0
*********************/

/******************
两个操作，合并两堆，或者取掉1个
******************/
最后肯定合并成一堆再一个个取
如果全大于1，先手可以保证NIM胜利的情况下先合并
不全为1，后手可以取完一个一堆的，相当于操作了两次。
此时，DFS+记忆化搜索来解决
dp[i][j]当1的个数为i时，其他全合并起来一共j个
其中的操作包括：
把某堆只有一个的，取走
把两堆只有一个的，合并
把某堆只有一个的，合并给不是一个的
把不是一个的，取走一个
int dfs(int i, int j) {  
    if (dp[i][j] != -1) return dp[i][j];  
    if (j == 1) return dp[i][j] = dfs(i+1, 0);  
    dp[i][j] = 0;  
    if (i >= 1 && !dfs(i-1, j)) dp[i][j] = 1;  
    else if (j >= 1 && !dfs(i, j-1)) dp[i][j] = 1;  
    else if (i >= 1 && j > 0 && !dfs(i-1, j+1)) dp[i][j] = 1;  
    else if (i >= 2 && ((j >= 1 && !dfs(i-2, j+3)) || (j == 0 && !dfs(i-2, 2))))  
        dp[i][j] = 1;  
    return dp[i][j];  
}

/****************
31 游戏
1~6各4张
****************/
直接搜索，据说记忆化也不用

反nim问题

这题与以往的博弈题的胜负条件不同，谁先走完最后一步谁输，但他也是一类Nim游戏，即为anti-nim游戏。
首先给出结论：先手胜当且仅当
①所有堆石子数都为1且游戏的SG值为0（即有偶数个孤单堆-每堆只有1个石子数）；
②存在某堆石子数大于1且游戏的SG值不为0.

数论

fibonacci数列的性质：

1.gcd(fib(n),fib(m))=fib(gcd(n,m))
证明：可以通过反证法先证fibonacci数列的任意相邻两项一定互素，然后可证n>m时gcd(fib(n),fib(m))=gcd(fib(n-m),fib(m))，递归可求gcd(fib(n),fib(m))=gcd(fib(k),fib(l))，最后k=l，不然继续递归。K是通过展转相减法求出，易证k=gcd(n,m)，所以gcd(fib(n),fib(m))=fib(gcd(n,m))。
2.如果fib(k)能被x整除，则fib(k*i)都可以被x整除。
3.f(0)+f(1)+f(2)+…+f(n) = f(n+2)-1
4.f(1)+f(3)+f(5)+…+f(2n-1) = f(2n)
5.f(2)+f(4)+f(6)+…+f(2n) = f(2n+1)-1
6.[f(0)]^2+[f(1)]^2+…+[f(n)]^2 = f(n)·f(n+1)
7.f(0)-f(1)+f(2)-…+(-1)^n·f(n) = (-1)^n·[f(n+1)-f(n)]+1
8.f(n+m) = f(n+1)·f(m)+f(n)*f(m-1)
9.[f(n)]^2 = (-1)^(n-1)+f(n-1)·f(n+1)
10.f(2n-1) = [f(n)]^2-[f(n-2)]^2
11.3f(n) = f(n+2)+f(n-2)
12.f(2n-2m-2)[f(2n)+f(2n+2)] = f(2m+2)+f(4n-2m) [ n〉m≥-1,且n≥1]

表为平方和问题以及佩尔方程求解

1 费马平方和定理
奇质数能表示为两个平方数之和的充分必要条件是该素数被4除余1
2 费马平方和定理的拓展定理
正整数能表示为两平方数之和的充要条件是在它的标准分解式中，形如素因子的指数是偶数
3 Brahmagupta–Fibonacci identity
如果两个整数都能表示为两个平方数之和，则它们的积也能表示为两个平方数之和。公式及拓展公式为

从这个定理可以看出：如果n不能表示为三个数的平方和，那么n也就不能表示为两个数的平方和。
4 四平方和定理
每个正整数都可以表示成四个整数的平方数之和
5 表为3个数的平方和条件
正整数能表示为三个数的平方和的充要条件是n不能表示成4^m*(8*k+7)的形式。
6 本原勾股数
本原勾股数组（PPT)是一个三元组（a，b，c),其中a，b，c无公因数，且满足a^2 + b^2 =c^2。
s,t为奇数(s > t >= 1)，并且gcd(s,t) == 1,那么a = st; b = (s*s-t*t); c = (s*s+t*t)/2;
7 佩尔方程形如x^2-D*y^2=1(D是一个固定的正整数且D不是完全平方数)的方程称为佩尔方程
佩尔方程总有正整数解，若(x1,y1)是使x1最小的解，则每个解(xk,yk)都可以通过取幂得到： 
xk + yk*sqrt(D) = (x1 + y1*sqrt(D))^k 
也有：xn+1 = x0*xn + D*y0*yn, yn+1 = y0*xn + x0*yn; 
xn+2 = 2x0*xn+1-xn,yn+2 = 2x0*yn+1-yn

反素数

给一个数n，求一个最小的正整数，使得它的因子个数为n。

int p[16] = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53};
LL n, ans;
void dfs(int dept, ULL tmp, int num){
    if(num > n) return;
    if(num == n && ans > tmp) ans = tmp;
    for(int i=1;i<=63;i++){
        if(ans / p[dept] < tmp) break;
        dfs(dept+1,tmp *= p[dept], num*(i+1));
    }
}
int main(){
    while(cin>>n){
        ans = INF;
        dfs(0,1,1);
        cout << ans << endl;
    }
    return 0;
}

欧拉筛

#include 
using namespace std;
int prime[1100000],primesize,phi[11000000];
bool isprime[11000000];

void getlist(int listsize){
    memset(isprime, 1, sizeof(isprime));
    isprime[1] = false;
    for(int i=2;i<=listsize;i++){
        if(isprime[i]) prime[++primesize]=i;
         for(int j = 1; j <= primesize && i*prime[j] <= listsize;j++){
            isprime[i*prime[j]] = false;
            if(i%prime[j] == 0) break;
         }
    }
}

莫比乌斯函数模板

void Init(){
    memset(vis,0,sizeof(vis));
    mu[1] = 1;
    cnt = 0;
    for(int i=2; i

乘法逆元

//扩展欧几里得（扩展gcd）  
LL ex_gcd(LL a,LL b,LL &x,LL &y){  
    if (a == 0 && b == 0) return -1;  
    if (b == 0){x = 1; y = 0; return a;}  
    LL d=ex_gcd(b, a % b, y, x);  
    y -= a / b * x;  
    return d;
}  
//乘法逆元 
LL mod_inverse(LL a,LL n){   
    LL x,y;
    LL d = ex_gcd(a,n,x,y);  
    return (x % n + n) % n;  
} 
//p是质数可以 快速幂p-2
LL quick_mod(LL a, LL b){  
    LL ans = 1;
    a %= MOD;
    for(;b; b >>= 1, a = a*a % MOD){
        if(b & 1) ans = ans * a % MOD;
    }
    return ans;
}
//逆元筛：求1-MAXN的所有关于MOD的逆元
inv[0] = 0; inv[1] = 1;
for(i = 2; i < MAXN; i++){  
    inv[i] = inv[MOD % i] * (MOD - MOD / i) % MOD;  
    f[i] = (f[i-1] * i) % MOD;  
}

二次同余方程的解

LL quick_mod(LL a, LL b, LL m){}  //快速幂
struct T  { LL p, d; }; 
LL w;  
  
//二次域乘法  
T multi_er(T a, T b, LL m)  {  
    T ans;  
    ans.p = (a.p * b.p % m + a.d * b.d % m * w % m) % m;  
    ans.d = (a.p * b.d % m + a.d * b.p % m) % m;  
    return ans;  
}  
  
//二次域上快速幂  
T power(T a, LL b, LL m) {  
    T ans;  
    ans.p = 1;  
    ans.d = 0;  
    while(b)  {  
        if(b & 1)  {  
            ans = multi_er(ans, a, m);  
            b--;  
        }  
        b >>= 1;  
        a = multi_er(a, a, m);  
    }  
    return ans;  
}  
  
//求勒让德符号  
LL Legendre(LL a, LL p)  {  
    return quick_mod(a, (p-1)>>1, p);  
}  
  
LL mod(LL a, LL m)  {  
    a %= m;  
    if(a < 0) a += m;  
    return a;  
}  
  
LL Solve(LL n,LL p)  {  
    if(p == 2) return 1;  
    if (Legendre(n, p) + 1 == p)  return -1;  
    LL a = -1, t;  
    while(true){  
        a = rand() % p;  
        t = a * a - n;  
        w = mod(t, p);  
        if(Legendre(w, p) + 1 == p) break;  
    }  
    T tmp;  
    tmp.p = a;  
    tmp.d = 1;  
    T ans = power(tmp, (p + 1)>>1, p);  
    return ans.p;  
}  
  
int main(){  
    int t;  scanf("%d", &t);  
    while(t--){  
        int n, p;  
        scanf("%d %d",&n,&p);  
        n %= p;  
        int a = Solve(n, p);  
        if(a == -1){  
            puts("No root");  
            continue;  
        }  
        int b = p - a;  
        if(a > b) swap(a, b);  
        if(a == b)  
            printf("%d\n",a);  
        else  
            printf("%d %d\n",a,b);  
    }  
    return 0;  
}  

预处理所有数的因数

//预处理所有数的因数表
//SPEED: ECNUOJ 1E6 5000MS O(nlogn)
const int N = 100000 + 5;
vector factor[N];
void init(){
    for(int i = 2; i < N; i ++){ 
        for(int j = i; j < N; j += i){
            factor[j].push_back(i); 
        }
    }
}
//预处理质因数表
vector x[N];  
bool is[N];  
void prime() {  
    memset(is, false, sizeof(is));  
    for (int i=0; i

随机素数测试和大数分解(POJ 1811)

/***************************************************
* Miller_Rabin 算法进行素数测试
* 速度快，可以判断一个 < 2^63 的数是不是素数
****************************************************/
const int S = 8; //随机算法判定次数，一般8~10就够了
// 快速乘法，计算ret = (a*b)%c a,b,c < 2^63
long long mult_mod(long long a,long long b,long long c)
// 快速幂，计算 ret = (a^n)%mod
long long pow_mod(long long a,long long n,long long mod)
// 通过 a^(n-1)=1(mod n)来判断n是不是素数
// n-1 = x*2^t 中间使用二次判断
// 是合数返回true, 不一定是合数返回false
bool check(long long a,long long n,long long x,long long t){
    long long ret = pow_mod(a,x,n);
    long long last = ret;
    for(int i = 1; i <= t; i++){
        ret = mult_mod(ret,ret,n);
        if(ret == 1 && last != 1 && last != n-1)return true;//合数
        last = ret;
    }
    if(ret != 1)return true;
    else return false;
}
//**************************************************
// Miller_Rabin算法
// 是素数返回true,(可能是伪素数)
// 不是素数返回false
//**************************************************
bool Miller_Rabin(long long n){
    if (n < 2) return false;
    if (n == 2) return true;
    if ((n&1) == 0) return false;//偶数
    long long x = n - 1, t = 0;
    for(; (x&1)==0;){x >>= 1; t++;}
    srand(time(NULL));/* *************** */
    for(int i = 0; i < S; i++){
        long long a = rand()%(n-1) + 1;
        if( check(a,n,x,t) ) return false;
    }
    return true;
}
//**********************************************
// pollard_rho 算法进行质因素分解
//*********************************************
long long factor[100];//质因素分解结果（刚返回时时无序的）
int tol;//质因素的个数，编号0~tol-1
long long gcd(long long a,long long b)
//找出一个因子
long long pollard_rho(long long x,long long c){
    long long i = 1, k = 2;
    srand(time(NULL));
    long long x0 = rand()%(x-1) + 1;
    long long y = x0;
    while(1){
        i ++;
        x0 = (mult_mod(x0,x0,x) + c)%x;
        long long d = gcd(y - x0,x);
        if( d != 1 && d != x)return d;
        if(y == x0) return x;
        if(i == k){y = x0; k += k;}
    }
}
//对 n进行素因子分解，存入factor. k设置为107左右即可
void findfac(long long n,int k){
    if(n == 1)return;
    if(Miller_Rabin(n)){
        factor[tol++] = n;
        return;
    }
    long long p = n;
    int c = k;
    while( p >= n) p = pollard_rho(p,c--);//值变化，防止死循环k
    findfac(p,k);
    findfac(n/p,k);
}
//POJ 1811
//给出一个N(2 <= N < 2^54),如果是素数，输出"Prime",否则输出最小的素因子
int main(){
    int T; scanf("%d",&T); long long n;
    while(T--){
        scanf("%I64d",&n);
        if(Miller_Rabin(n)) printf("Prime\n");
        else{
            tol = 0;
            findfac(n,107);
            long long ans = factor[0];
            for(int i = 1; i < tol; i++)
                ans = min(ans,factor[i]);
            printf("%I64d\n",ans);
        }
    }
    return 0;
}

中国剩余定理

//可以不满足两两互质
int n;
//扩展gcd多了一个变量
void ex_gcd(LL a, LL b, LL &d, LL &x, LL &y){
    if (!b) {d = a, x = 1, y = 0;}
    else{
        ex_gcd(b, a % b, d, y, x);
        y -= x * (a / b);
    }
}
LL ex_crt(LL *m, LL *r, int n){
    LL M = m[1], R = r[1], x, y, d;
    for (int i = 2; i <= n; ++i){
        ex_gcd(M, m[i], d, x, y);
        if ((r[i] - R) % d) return -1;
        x = (r[i] - R) / d * x % (m[i] / d); //m[i]为LL范围时，此处会爆LL
        R += x * M;
        M = M / d * m[i];
        R %= M;
    }
    return R > 0 ? R : R + M;
}

离散对数（关于方程x^A=B(mod C)的解)

首先判断是否有解，即 a,p 是否互质。不互质即无解。不妨令 x = im − j, 其中
m = ⌈ √ q⌉ , 这样问题变为求得一组 i j 使得条件满足。此时原式变为 a im−j ≡ b (Mod p), 移
项化简得 (a m ) i ≡ ba j (Mod p)。这个时候我们只需穷举 i,j 使得式子成立即可。先从让 j 从
[0,m] 中穷举，并用 hash 记录下 ba j 对应的 j 值。相同的 ba j 记录较大的 j. 接着让 i 从 [1,m]
中穷举，如果 (a m ) i 在 hash 表中有对应的 j 存在，则对应的 im − j 是一组解。其中第一次出
现的为最小的解。

map Hash;
LL i, j;
LL bsgs(LL a, LL b, LL p){
    LL xx, yy;
    if (exgcd(a, p, xx, yy) != 1)return −1;
    a %= p;
    LL m = ceil(sqrt(p));
    Hash.clear();
    LL tmp, ans = b % p;
    for (int i = 0; i <= m; ++i){
        Hash[ans] = i;
        ans = ans * a % p;
    }
    tmp = f(a, m, p);
    ans = 1;
    for (int i = 1; i <= m; ++i){
        ans = ans * tmp % p;
        if (Hash[ans] != 0) return i * m − Hash[ans];
    }
    return −1;
}

字符串

字符串EL哈希

from AcDreamer

unsigned int ELFhash(char *str){  
    unsigned int h = 0;  
    unsigned int x;  
    while(*str){  
        h = (h << 4) + *str++;  
        x = h & 0xF0000000L;  
        if(x){  
            h ^= x>>24;  
            h &= ~x;  
        }  
    }  
    return h & 0x7FFFFFFF;  
}  

双哈希

const ll p1=4373,p2=4789;
const ll mod1=998244353,mod2=1e9+7;
const int N=4096;
ll xp1[27],xp2[27];
ll h1[2][N],h2[2][N];
int len1,len2;
char s[N];
mapH1,H2;
bool check(int x){
    H1.clear();
    H2.clear();
    for (int i=1;i<=len1;i++){
        if (i+x-1>len1) break;
        int t1=(h1[0][i+x-1]-h1[0][i-1]+mod1)%mod1;
        int t2=(h1[1][i+x-1]-h1[1][i-1]+mod2)%mod2;
        H1[t1]=1;
        H2[t2]=1;
    }
    for (int i=1;i<=len2;i++){
        if (i+x-1>len2) break;
        int t1=(h2[0][i+x-1]-h2[0][i-1]+mod1)%mod1;
        int t2=(h2[1][i+x-1]-h2[1][i-1]+mod2)%mod2;
        if (H1[t1]!=0&&H2[t2]!=0) return 1;
    }
    return 0;
}
int main(){
    xp1[0]=xp2[0]=1;
    for (int i=1;i<=26;i++){
        xp1[i]=(1ll*xp1[i-1]*p1)%mod1;
        xp2[i]=(1ll*xp2[i-1]*p2)%mod2;
    }
    scanf("%s",s+1);
    len1=strlen(s+1);
    for (int i=1;i<=len1;i++){
        h1[0][i]=(h1[0][i-1]+xp1[s[i]-'a'])%mod1;
        h1[1][i]=(h1[1][i-1]+xp2[s[i]-'a'])%mod2;
    }
    scanf("%s",s+1);
    len2=strlen(s+1);
    for (int i=1;i<=len2;i++){
        h2[0][i]=(h2[0][i-1]+xp1[s[i]-'a'])%mod1;
        h2[1][i]=(h2[1][i-1]+xp2[s[i]-'a'])%mod2;
    }
    int ans;
    for (ans=min(len1,len2);ans>=0;ans--){
        if (ans==0)
            printf("%d\n",ans);
        else{
            if (check(ans)){
                printf("%d\n",ans);
                return 0;
            }
        }
    }
    return 0;
}

Manacher算法（回文串）

#include
#include
#include
#include
#include
using namespace std;
const int N=233333;//20W

//在o(n)时间内算出以每个点为中心的最大回文串长度
int Manacher(string st){
    int len = st.size();
    int *p = new int[len+1];
    memset(p,0,sizeof(p));
    int mx = 0,id = 0;
    for (int i = 1;i <= len; i++){
        if (mx > i) p[i] = min(p[2*id-i],mx-i);
        else p[i] = 1;
        while (st[i+p[i]] == st[i-p[i]]) p[i]++;
        if (i + p[i] > mx){mx = i + p[i]; id = i;}
    }
    int ma = 0;
    for (int i = 1; i < len; i++) ma = max(ma, p[i]);
    delete(p);
    return ma - 1;
}

int main(){
    //freopen("fuck.in","r",stdin);
    char st[N];
    while (~scanf("%s",st)){
        string st0="$#";
        for (int i=0; st[i] != '\0'; i++){
            st0 += st[i]; st0 += "#";
        }
        printf("%d\n", Manacher(st0));
    }
    return 0;
}

KMP（字符串匹配）

#include
#include
using namespace std;
typedef long long LL;
const int N=100007;
const int P=1000000007;
char a[N],b[N];
bool mat[N];
int Next[N];//一定要Next,next会CE
LL f[N];

void getNext(int m, char b[]){
    int i = 0,j = -1;
    Next[0] = -1;
    while (i < m){
        if (j == -1 || b[i] == b[j]){
            if (b[++i] != b[++j]) Next[i]=j;
            else Next[i] = Next[j];
        }else j = Next[j];
    }
}
//主程序里每组数据需要memset a,b数组!!!
void KMP(int n,char a[], int m, char b[]){
    memset(mat, 0, sizeof(mat));
    int i = 0, j = 0;
    getNext(m, b);//这行视情况可以放在main里面
    while (i < n && j < m){
        if (j == -1 || a[i] == b[j]) i++, j++;
        else j = Next[j];
        if (!i && !j)break;
        if (j == m){
            mat[i] = 1;
            //printf("mat[%d]get\n",i);
            j = Next[j];
        }
    }
}

01Tire树

//01字典树的实现可以看成是把一个数的二进制字符化后插入到一颗一般的字典树中
//查找最大异或值的时候我们是从最高位 向下贪心查找 贪心策略为：当前查找第k位 二进制数位IDX 如果存在IDX ^ 1的节点 我们就进入这个节点 否则进入IDX节点 
const int maxn = 100000 + 5;        //集合中的数字个数
typedef long long LL;
int ch[32 * maxn][2];               //节点的边信息
LL value[32 * maxn];                //节点存储的值
int node_cnt;                       //树中当前节点个数

inline void init(){                 //树清空
    node_cnt = 1;
    memset(ch[0],0,sizeof(ch));
}           

inline void Insert(LL x){           //在字典树中插入 X    
                                    //和一般字典树的操作相同 将X的二进制插入到字典树中
    int cur = 0;
    for(int i = 32;i >= 0;--i){
        int idx = (x >> i) & 1;
        if(!ch[cur][idx]){
            memset(ch[node_cnt],0,sizeof(ch[node_cnt]));
            ch[cur][idx] = node_cnt;
            value[node_cnt++] = 0;
        }
        cur = ch[cur][idx];
    }
    value[cur] = x;             //最后的节点插入value
}

inline LL Query(LL x){              //在字典树中查找和X异或的最大值的元素Y 返回Y的值
    int cur = 0;
    for(int i = 32;i >= 0;--i){
        int idx = (x >> i) & 1;
        if(ch[cur][idx ^ 1]) cur = ch[cur][idx ^ 1];
        else cur = ch[cur][idx];
    }
    return value[cur];
}

Tire树_刘汝佳

// LA3942 Remember the Word
// Rujia Liu
#include
#include
using namespace std;

const int maxnode = 4000 * 100 + 10;
const int sigma_size = 26;

// 字母表为全体小写字母的Trie
struct Trie {
  int ch[maxnode][sigma_size];
  int val[maxnode];
  int sz; // 结点总数
  void clear() { sz = 1; memset(ch[0], 0, sizeof(ch[0])); } // 初始时只有一个根结点
  int idx(char c) { return c - 'a'; } // 字符c的编号

  // 插入字符串s，附加信息为v。注意v必须非0，因为0代表“本结点不是单词结点”
  void insert(const char *s, int v) {
    int u = 0, n = strlen(s);
    for(int i = 0; i < n; i++) {
      int c = idx(s[i]);
      if(!ch[u][c]) { // 结点不存在
        memset(ch[sz], 0, sizeof(ch[sz]));
        val[sz] = 0;  // 中间结点的附加信息为0
        ch[u][c] = sz++; // 新建结点
      }
      u = ch[u][c]; // 往下走
    }
    val[u] = v; // 字符串的最后一个字符的附加信息为v
  }

  // 找字符串s的长度不超过len的前缀
  void find_prefixes(const char *s, int len, vector& ans) {
    int u = 0;
    for(int i = 0; i < len; i++) {
      if(s[i] == '\0') break;
      int c = idx(s[i]);
      if(!ch[u][c]) break;
      u = ch[u][c];
      if(val[u] != 0) ans.push_back(val[u]); // 找到一个前缀
    }
  }
};

#include
const int maxl = 300000 + 10; // 文本串最大长度
const int maxw = 4000 + 10;   // 单词最大个数
const int maxwl = 100 + 10;   // 每个单词最大长度
const int MOD = 20071027;

int d[maxl], len[maxw], S;
char text[maxl], word[maxwl];
Trie trie;

int main() {
  int kase = 1;
  while(scanf("%s%d", text, &S) == 2) {
    trie.clear();
    for(int i = 1; i <= S; i++) {
      scanf("%s", word);
      len[i] = strlen(word);
      trie.insert(word, i);
    }
    memset(d, 0, sizeof(d));
    int L = strlen(text);
    d[L] = 1;
    for(int i = L-1; i >= 0; i--) {
      vector p;
      trie.find_prefixes(text+i, L-i, p);
      for(int j = 0; j < p.size(); j++)
        d[i] = (d[i] + d[i+len[p[j]]]) % MOD;
    }
    printf("Case %d: %d\n", kase++, d[0]);
  }
  return 0;
}

压缩Tire树

// UVa11732 strcmp() Anyone?  
// Rujia Liu  
#include  
#include  
#include  
using namespace std;
const int maxnode = 4000 * 1000 + 10;  
const int sigma_size = 26;  
  
// 字母表为全体小写字母的Trie  
struct Trie {  
  int head[maxnode]; // head[i]为第i个结点的左儿子编号  
  int next[maxnode]; // next[i]为第i个结点的右兄弟编号  
  char ch[maxnode];  // ch[i]为第i个结点上的字符  
  int tot[maxnode];  // tot[i]为第i个结点为根的子树包含的叶结点总数  
  int sz; // 结点总数  
  long long ans; // 答案  
  void clear() { sz = 1; tot[0] = head[0] = next[0] = 0; } // 初始时只有一个根结点  
  
  // 插入字符串s（包括最后的'\0'），沿途更新tot  
  void insert(const char *s) {  
    int u = 0, v, n = strlen(s);  
    tot[0]++;  
    for(int i = 0; i <= n; i++) {  
      // 找字符a[i]  
      bool found = false;  
      for(v = head[u]; v != 0; v = next[v])  
        if(ch[v] == s[i]) { // 找到了  
          found = true;  
          break;  
        }  
      if(!found) {  
        v = sz++; // 新建结点  
        tot[v] = 0;  
        ch[v] = s[i];  
        next[v] = head[u];  
        head[u] = v; // 插入到链表的首部  
        head[v] = 0;  
      }  
      u = v;  
      tot[u]++;  
    }  
  }  
  
  // 统计LCP=u的所有单词两两的比较次数之和  
  void dfs(int depth, int u) {  
    if(head[u] == 0) // 叶结点  
      ans += tot[u] * (tot[u] - 1) * depth;  
    else {  
      int sum = 0;  
      for(int v = head[u]; v != 0; v = next[v])  
        sum += tot[v] * (tot[u] - tot[v]); // 子树v中选一个串，其他子树中再选一个  
      ans += sum / 2 * (2 * depth + 1); // 除以2是每种选法统计了两次  
      for(int v = head[u]; v != 0; v = next[v])  
        dfs(depth+1, v);  
    }  
  }
  
  long long count() {  // 统计  
    ans = 0;  
    dfs(0, 0);  
    return ans;  
  }  
} trie;  
  
const int maxl = 1000 + 10;   // 每个单词最大长度  
int n;
char word[maxl];

int main() {  
  int kase = 1;  
  while(scanf("%d", &n) == 1 && n) {  
    trie.clear();  
    for(int i = 0; i < n; i++) {  
      scanf("%s", word);  
      trie.insert(word);  
    }  
    printf("Case %d: %lld\n", kase++, trie.count());  
  }  
  return 0;  
} 

AC自动机

// LA4670 Dominating Patterns
// Rujia Liu
#include
#include
#include
#include

###后缀数组

/*
后缀数组 DA(倍增)算法求 SA[N] 与 Rank[N] （时间O(NlogN）,空间O(N)）
sa[i] : 表示 排在第i位的后缀 起始下标
rank[i] : 表示后缀 suffix(i)排在第几
height[i] : 表示 sa[i-1] 与 sa[i] 的LCP 值
h[i]: 表示 suffix(i)与其排名前一位的 LCP值
*/
const int N = 100005;
int wa[N],wb[N],wv[N],ws[N];
int cmp(int *r,int a,int b,int l){
    return r[a]==r[b]&&r[a+l]==r[b+l];
}
void da(int *r,int *sa,int n,int m){
    int i,j,p,*x=wa,*y=wb;
    // 下面四行是对第一个字母的一个基数排序：基数排序其实就是记录前面有多少个位置被占据了 
    for(i=0;i=0;i--) sa[--ws[x[i]]]=i; // 根据位置来排序，sa[x] = i，表示i位置排在第x位
    // wa[x[i]]就是字符集0-x[i]共有多少字符占据了位置，减去自己的一个位置剩下的就是自己的排名了，排名从0开始 
    // 排名过程中主要的过程是对于处于相同字符的字符的排序，因为改变wa[x[i]]值得只会是本身，小于该字符的贡献值
    // 是不变的，对于第一个字符相同的依据是位置关系，在后面将看到通过第二个关键字来确定相同字符的先后关系 
    
    // 这以后的排序都是通过两个关键字来确定一个串的位置，也即倍增思想
    // 通过将一个串分解成两部分，而这两部分的位置关系我们都已经计算出来 
    for(j=1,p=1;p=j) y[p++]=sa[i]-j; // sa[i]-j开头的串作为第二关键字与编号为sa[i]的串匹配，sa[i]=0;i--) sa[--ws[wv[i]]]=y[i]; // 按照第二关键字进行第一关键字的基数排序 
        for(swap(x,y),p=1,x[sa[0]]=0,i=1;i=0;i--) b[--ws[wv[i]]]=a[i];
    return;
}
void dc3(int *r,int *sa,int n,int m){ //涵义与DA 相同
    int i,j,*rn=r+n,*san=sa+n,ta=0,tb=(n+1)/3,tbc=0,p;
    r[n]=r[n+1]=0;
    for(i=0;i

SAM

最长公共子串O（n）

//后缀自动机求最长公共子串，复杂度O(n)
const int maxn = 250010;
const int SIGMA_SIZE = 26;
struct SAM_Node{
    SAM_Node *par,*Next[SIGMA_SIZE];
    int len,id,pos;
    SAM_Node(){}
    SAM_Node(int _len){
        par = 0;
        len = _len;
        memset(Next, 0, sizeof(Next));
    }
};
SAM_Node node[maxn*2],*root,*last;
int SAM_size;
SAM_Node *newSAM_Node(int len){
    node[SAM_size] = SAM_Node(len);
    node[SAM_size].id = SAM_size;
    return &node[SAM_size++];
}
SAM_Node *newSAM_Node(SAM_Node *p){
    node[SAM_size] = *p;
    node[SAM_size].id = SAM_size;
    return &node[SAM_size++];
}
void SAM_init(){
    SAM_size = 0;
    root=last = newSAM_Node(0);
    node[0].pos = 0;
}
void SAM_add(int x,int len){
    SAM_Node *p = last, *np = newSAM_Node(p->len+1);
    np->pos = len;
    last = np;
    while(p&&!p->Next[x]){
        p->Next[x] = np;
        p = p->par;
    }
    if(!p){
        np->par = root;
        return;
    }
    SAM_Node *q=p->Next[x];
    if(q->len == p->len+1){
        np->par = q;
        return ;
    }
    SAM_Node *nq=newSAM_Node(q);
    nq->len = p->len+1;
    q->par = nq;
    np->par = nq;
    while(p&&p->Next[x] == q){
        p->Next[x]=nq;
        p=p->par;
    }
}
void SAM_build(char *s){
    SAM_init();
    int le = strlen(s);
    for(int i = 0; i < le; i++) SAM_add(s[i]-'a', i+1);
}
int solve(char* str1,char* str2,int x){
    SAM_build(str1);
    SAM_Node *tmp=root;
    int le = strlen(str2);
    int cnt = 0, ans = 0;
    for(int i=0;iNext[c]) tmp = tmp->Next[c],cnt++;
        else{
            while(tmp && !tmp->Next[c]) tmp = tmp->par;
            if (!tmp) tmp = root,cnt=0;
            else{
                cnt = tmp->len+1;
                tmp = tmp->Next[c];
            }
        }
        ans = max(ans, cnt); //cnt为str2以第i位为结尾与str1的最长公共子串 
    }
    return ans;
}

数据结构

st表

nlogn 区间rmq，只有查询没有修改

int st[N][K], a[N], log_2[N];
inline void ini_st(){
    log_2[1] = 0;
    for(int i = 2; i <= n; ++i){
        log_2[i] = log_2[i-1];
        if((1<

树状数组(逆序对)

#include 
#include 
#include 
#include 
using namespace std;
const int N = 1e5 + 7;

struct binaryIndexTree{
	int val[N], n;
	inline void init(int n){
		this->n = n;
		memset(val, 0, sizeof(val));
	}
	inline void add(int k, int num){
		for (;k <= n; k += k&-k) val[k] += num;
	}
	int sum(int k){
		int sum = 0;
		for (; k; k -= k&-k) sum += val[k];
		return sum;
	}
	int Getsum(LL x1,LL x2){ //求任意区间和
		return sum(x2) - sum(x1-1);
	}
} T;

int arr[N], n;

int main(){
	//freopen("in.txt", "r", stdin); 
	for (; ~scanf("%d", &n);){
		T.init(n);
		int sum = 0;
		for (int i = 0; i < n; i++){
			scanf("%d", &arr[i]);
			arr[i]++;
			sum += T.sum(n) - T.sum(arr[i] - 1);
			T.add(arr[i], 1);
		}
		int ans = sum;
		for (int i = 0; i < n; i++){
			sum += (n - arr[i]) - (arr[i] - 1);
			ans = min(ans, sum);
		}
		printf("%d\n", ans);
	}
}

二维树状数组

Codeforces 869E

题意：在一个n×m的方格板上，操作1将一个矩形区域的边界上加上一圈障碍，操作2将一个矩形区域的边界上的障碍移除，操作3询问两点是否能不越过障碍互相到达。题目保证任意两圈矩形障碍不会相交。
思路：很容易想到二维树状数组实现区间更新点查询，但是如果只是简单的+1，-1更新的话是无法判断出两点是否可以不经过障碍可达的。因此我们要把每一圈障碍都哈希出一个不同的值，这样点查询的时候只要判断两个点的值是否相同就行了。

#include  
#define ll long long  
#define lowbit(x) (x & -x)  
#define MAXN 2525   
using namespace std;  
ll bit[MAXN][MAXN];  
int n, m;  
void add(int i, int j, ll delta){  
    for(int x = i; x < n + 10; x += lowbit(x))  
    for(int y = j; y < m + 10; y += lowbit(y))  
    bit[x][y] += delta;  
}  
ll sum(int i, int j){  
    ll ans = 0;  
    for(int x = i; x; x -= lowbit(x))  
    for(int y = j; y; y -= lowbit(y))  
    ans += bit[x][y];  
    return ans;  
}  
void update(int r1, int c1, int r2, int c2, ll delta){  
    add(r1, c1, delta);  
    add(r1, c2 + 1, -delta);  
    add(r2 + 1, c1, -delta);  
    add(r2 + 1, c2 + 1, delta);   
}  
int main(){  
    int q, t, r1, c1, r2, c2;  
    cin >> n >> m >> q;  
    while(q--){  
        scanf("%d %d %d %d %d", &t, &r1, &c1, &r2, &c2);  
        if(t != 3){  
            ll delta = r1;  
            delta = delta * 111 + c1;  
            delta = delta * 111 + r2;  
            delta = delta * 111 + c2;  
            delta *= (t == 1) ? 1 : -1;  
            update(r1, c1, r2, c2, delta);  
        }  
        else puts(sum(r1, c1) == sum(r2, c2) ? "Yes" : "No");  
    }  
    return 0;  
}  

ZKW线段树（单点修改）

线段树M的计算M = (1 << (int)(ceil)(log(i)/log(2))) - 1，就不一个一个改了

#include 
#include 
#include 
#include 
using namespace std;
const int N = 2e5 + 7;

struct segmentTree{
	#define lc (t<<1)
	#define rc (t<<1^1)
	int sum[N], M;

	inline void build(int n){
		M = (1 << (int)(ceil)(log(i)/log(2))) - 1;
		memset(sum, sizeof(sum), 0);
		for (int i = 1+M; i <= n+M; i++){
			scanf("%d", &sum[i]);
		}
		for (int t = M; t >= 1; t--){
			sum[t] = sum[lc] + sum[rc];
		}
	}

	void add(int t, int x){
		for (sum[t+=M]+=x, t>>=1; t; t>>=1){
			sum[t] = sum[lc] + sum[rc];
		}
	}

	int query(int l, int r){
		int ans = 0;
		for (l+=M-1,r+=M+1; l^r^1; l>>=1,r>>=1){
			if (~l&1) ans += sum[l^1];
			if ( r&1) ans += sum[r^1];
		}
		return ans;
	}
} T;

ZKW线段树（RMQ区间操作）

#include 
#include 
#include 
#include 
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
double EPS = 1e-11;
const LL INF = 0x3f3f3f3f3f3f3f3f;
int n, pos[N], arr[N], pre[N];

struct ZKWsegTree{
    double tree[N];
    int M, n;

    void build(int n, double Mid){
        this->n = n;
        M = 1; while (M < n) M <<= 1; if (M!=1) M--;
        for (int t = 1 ; t <= n; t++) tree[t+M] = 1.0*t*Mid;
        for (int t = n+1; t <= M+1; t++) tree[t+M] = INF;
        for (int t = M; t >= 1; t--) tree[t] = min(tree[t<<1], tree[t<<1^1]);
        for (int t = 2*M+1; t >= 1; t--) tree[t] = tree[t] - tree[t>>1];
    }

    void update(int l, int r, double val){
        double tmp;
        for (l+=M-1, r+=M+1; l^r^1; l>>=1, r>>=1){
            if (~l&1) tree[l^1] += val;
            if ( r&1) tree[r^1] += val;
            if (l > 1) tmp = min(tree[l], tree[l^1]), tree[l]-=tmp, tree[l^1]-=tmp, tree[l>>1]+=tmp;
            if (r > 1) tmp = min(tree[r], tree[r^1]), tree[r]-=tmp, tree[r^1]-=tmp, tree[r>>1]+=tmp;
        }
        for (; l > 1; l >>= 1){
            tmp = min(tree[l], tree[l^1]), tree[l]-=tmp, tree[l^1]-=tmp, tree[l>>1]+=tmp;
        }
        tree[1] += tree[0], tree[0] = 0;
    }

    double query(int l, int r){
        double lAns = 0, rAns = 0;
        l += M, r += M;
        if (l != r){
            for (; l^r^1; l>>=1, r>>=1){
                lAns += tree[l], rAns += tree[r];
                if (~l&1) lAns = min(lAns, tree[l^1]);
                if ( r&1) rAns = min(rAns, tree[r^1]);
            }
        }
        double ans = min(lAns + tree[l], rAns + tree[r]);
        for (;l > 1;) ans += tree[l>>=1];
        return ans;
    }
} T;

常规线段树（区间操作区间和）

#include 
#include 
#include 
#include 
using namespace std;
typedef long long LL;
const LL N = 5e5 + 7;

struct segTree{
	#define lc (rt<<1)
	#define rc (rt<<1^1)
	#define lson l, m, rt<<1
	#define rson m+1, r, rt<<1^1
	LL M, sum[N], tag[N];
	inline void build(LL n){
		M = 1; while(M= 1; rt--) sum[rt] = sum[lc] + sum[rc];
	}

	inline void pushUp(LL rt){
		sum[rt] = sum[lc] + sum[rc];
	}

	inline void pushDown(LL rt, LL len){
		if (tag[rt] == 0) return;
		tag[lc] += tag[rt];
		tag[rc] += tag[rt];
		sum[lc] += tag[rt] * (len>>1);
		sum[rc] += tag[rt] * (len>>1);
		tag[rt] = 0;
	}

	inline void update(LL L, LL R, LL x, LL l, LL r, LL rt){
		//printf("update(%d, %d, %d, %d, %d, %d)\n", L, R, x, l, r, rt);
		if (L <= l && r <= R){
			tag[rt] += x;
			sum[rt] += (r-l+1) * x;
			return;
		}
		pushDown(rt, r-l+1);
		LL m = (l + r) >> 1;
		if (L <= m) update(L, R, x, lson);
		if (m <  R) update(L, R, x, rson);
		pushUp(rt);
	}

	LL query(LL L, LL R, LL l, LL r, LL rt){
		if (L <= l && r <= R) return sum[rt];
		pushDown(rt, r-l+1);
		LL m = (l + r) >> 1;
		LL ans = 0;
		if (L <= m) ans += query(L, R, lson);
		if (m <  R) ans += query(L, R, rson);
		return ans;
	}
} T;

线段树的某些考点

双标记线段树+区间合并

hdu3397,int main 这里没贴，傻子都能写出来

#include 
#include 
#include 
#include 
#include 
using namespace std;
const int N = 262144 + 7;
int arr[N];

// 0: 将区间[a,b]之间的数全部置为0
// 1: 将区间[a,b]之间的数全部置为1
// 2: 将区间[a,b]之间的 1->0  0->1
// 3: 求区间[a,b]之间1的个数
// 4: 求区间[a,b]之间1的最长连续长度

struct segTree{
    #define lc (rt<<1)
    #define rc (rt<<1^1)
    #define lson l, m, rt<<1
    #define rson m+1, r, rt<<1^1
    int M; // number of no-leaf nodes
    int lsum[N][2], msum[N][2], rsum[N][2], nsum[N]; // values
    int vert[N], lazy[N]; // tags

    // 赋值操作，结束后记得清空vert标记
    inline void setTag(const int &rt, const int &val, const int &len){
        nsum[rt] = val ? len : 0;
        lsum[rt][0] = msum[rt][0] = rsum[rt][0] = val ? 0 : len;
        lsum[rt][1] = msum[rt][1] = rsum[rt][1] = val ? len : 0;
        lazy[rt] = val;
        vert[rt] = 0;
    }

    // 对rt节点进行取反操作，swap 0 和 1 的值
    inline void vertTag(const int &rt, const int &len){
        nsum[rt] = len - nsum[rt];
        swap(lsum[rt][0], lsum[rt][1]);
        swap(msum[rt][0], msum[rt][1]);
        swap(rsum[rt][0], rsum[rt][1]);
        vert[rt] ^= 1;
    }

    //区间合并的pushUp大体都这么写
    inline void pushUp(const int &rt, const int &len){
        nsum[rt] = nsum[lc] + nsum[rc];
        for (int i = 0; i < 2; i++){
            lsum[rt][i] = lsum[lc][i];
            rsum[rt][i] = rsum[rc][i];
            if (lsum[rt][i] == len>>1) lsum[rt][i] += lsum[rc][i];
            if (rsum[rt][i] == len>>1) rsum[rt][i] += rsum[lc][i];
            msum[rt][i] = max(msum[lc][i], msum[rc][i]);
            msum[rt][i] = max(msum[rt][i], rsum[lc][i] + lsum[rc][i]);
        }
    }

    // 优先lazy标记，但是不要干扰vert标记
    // vert的时候进入vertTag必须保证lazy==-1
    inline void pushDown(const int &rt, const int &len){
        if (lazy[rt] != -1){
            setTag(lc, lazy[rt], len>>1);
            setTag(rc, lazy[rt], len>>1);
            vert[lc] = vert[rc] = 0;
        }
        if (vert[rt]){
            if (lazy[lc] != -1) setTag(lc, lazy[lc]^1, len>>1);
            else vertTag(lc, len>>1);
            if (lazy[rc] != -1) setTag(rc, lazy[rc]^1, len>>1);
            else vertTag(rc, len>>1);
            vert[rt] = 0;
        }
        lazy[rt] = -1;
    }

    inline void build(const int &n){
        M=1; for(;M1)M--;
        memset(vert, 0, sizeof vert);
        memset(lazy,-1, sizeof lazy);
        for (int i = 1; i <= M+1; i++){
            nsum[i+M] = i<=n ? arr[i] : 0;
            lsum[i+M][0] = msum[i+M][0] = rsum[i+M][0] = i<=n ?!arr[i] : 0;
            lsum[i+M][1] = msum[i+M][1] = rsum[i+M][1] = i<=n ? arr[i] : 0;
        }
        for (int rt = M, len = 2; rt >= 1; rt--) {
            pushUp(rt, len);
            if ((rt&(rt-1)) == (!rt)) len <<= 1;//O(1)判断2的整数次幂,dep--
        }
    }

    void update(int L, int R, int val, int l, int r, int rt){
        if (L <= l && r <= R){
            if (val != -1) setTag(rt, val, r-l+1);
            else { // invert
                if (lazy[rt] != -1) setTag(rt, lazy[rt]^1, r-l+1);
                else vertTag(rt, r-l+1);
            }
            return;
        }
        pushDown(rt, r-l+1);
        int m = (l + r) >> 1;
        if (L <= m) update(L, R, val, lson);
        if (m <  R) update(L, R, val, rson);
        pushUp(rt, r-l+1);
    }

    int sum(int L, int R, int l, int r, int rt){
        if (L <= l && r <= R) return nsum[rt];
        pushDown(rt, r-l+1);
        int m = (l + r) >> 1, ans = 0;
        if (L <= m) ans += sum(L, R, lson);
        if (m <  R) ans += sum(L, R, rson);
        return ans;
    }

    int query(int L, int R, int l, int r, int rt){
        if (L <= l && r <= R) return msum[rt][1];
        pushDown(rt, r-l+1);
        int m = (l + r) >> 1;
        // 区间合并的查询操作
        int ans = min(m-L+1, rsum[lc][1]) + min(R - m, lsum[rc][1]);
        if (L <= m) ans = max(ans, query(L, R, lson));
        if (m <  R) ans = max(ans, query(L, R, rson));
        return ans;
    }
    
    // have relation with int main, out API
    inline void setval(const int &l, const int &r, const int &val){
        update(l, r, val, 1, M+1, 1);
    }
    inline void invert(const int &l, const int &r){
        update(l, r,  -1, 1, M+1, 1);
    }
    inline int sum(const int &l, const int &r){
        return sum(l, r, 1, M+1, 1);
    }
    inline int query(const int &l, const int &r){ // continus
        return query(l, r, 1, M+1, 1);
    }
} T;

扫描线： 矩形面积并

HDU 1542

struct Seg{
    double l, r, h;  // height
    int s;  // status
    Seg(){}
    Seg(double x, double y, double z, int w): l(x), r(y), h(z), s(w){}
    bool operator < (const Seg & b) const {return h < b.h;}
} seg[N];
double ux[N];
int X, S;  // top of seg[] & ux[]

struct segTree{
    #define lc (rt<<1)
    #define rc (rt<<1^1)
    #define lson l, m, rt<<1
    #define rson m+1, r, rt<<1^1
    int cnt[N];
    double sum[N];

    inline void build(){
        memset(sum, 0, sizeof sum);
        memset(cnt, 0, sizeof cnt);
    }

    inline void pushUp(int rt, int l, int r){
        if (cnt[rt]) sum[rt] = ux[r+1] - ux[l];
        else sum[rt] = l==r ? 0 : sum[lc] + sum[rc];
    }

    void update(int L, int R, int x, int l, int r, int rt){
        if (L <= l && r <= R){
            cnt[rt] += x;
            pushUp(rt, l, r);
            return;
        }
        LL m = (l + r) >> 1;
        if (L <= m) update(L, R, x, lson);
        if (m <  R) update(L, R, x, rson);
        pushUp(rt, l, r);
    }
} T;

int Search(double key, int l, int r, double ux[]){
    for (; l <= r;){
        int m = (l + r) >> 1;
        if (ux[m] == key) return m;
        if (ux[m] < key) l = m + 1;
        else r = m -1;
    }
    return -1;
}

int main(){
    //freopen("in.txt", "r", stdin);
    for (int n, _ = 1; ~scanf("%d", &n) && n;){
        printf("Test case #%d\n", _++);
        X = S = 0;
        for (int i = 1; i <= n; i++){
            double l, low, r, high;
            scanf("%lf%lf%lf%lf", &l, &low, &r, &high);
            ux[++X] = l; ux[++X] = r;
            seg[++S] = Seg(l, r, low, 1);
            seg[++S] = Seg(l, r, high, -1);
        }
        sort(seg + 1, seg + S+1);
        sort(ux + 1, ux + X+1);
        X = unique(ux + 1, ux + X +1) - ux - 1;
        T.build();
        #define root 0, X+1, 1
        double ans = 0;
        for (int i = 1; i < S; i++){
            int l = Search(seg[i].l, 1, X, ux);
            int r = Search(seg[i].r, 1, X, ux) - 1;
            if (l <= r) T.update(l, r, seg[i].s, root);
            ans += T.sum[1] * (seg[i+1].h - seg[i].h);
        }
        printf("Total explored area: %.2lf\n\n", ans);
    }
    return 0;
}

扫描线， 矩形周长并

    int M, cnt[N], num[N], len[N];
    bool lbd[N], rbd[N];

    inline void pushUp(int rt, int l, int r){
        if (cnt[rt]) {
            lbd[rt] = rbd[rt] = 1;
            len[rt] = r - l + 1;
            num[rt] = 2;
        } else if (l == r) {
            len[rt] = num[rt] = lbd[rt] = rbd[rt] = 0;
        } else {
            lbd[rt] = lbd[lc];
            rbd[rt] = rbd[rc];
            len[rt] = len[lc] + len[rc];
            num[rt] = num[lc] + num[rc];
            if (lbd[rc] && rbd[lc]) num[rt] -= 2;
        }
    }

//calc
sort(seg + 1, seg + S+1);
int ans = 0, last = 0;
for (int i = 1; i <= S; i++, last = T.len[1]){
    T.update(seg[i].l, seg[i].r-1, seg[i].s, L, R-1, 1);
    ans += T.num[1] * (seg[i+1].h - seg[i].h);
    ans += abs(T.len[1] - last);
}

主席树

poj2104求区间k大值

# include 
# include 
# include 
# include 
using namespace std;
const int N = 1e5 + 7;
int arr[N];  //arr[]  原数组的数在rank[]中的位置;
int Rank[N]; //rank[] 原数组离散化

struct ChairTree{
    #define sum(x) tree[x].w
    #define lson tree[rt].lc, tree[rt1].lc, l, m
    #define rson tree[rt].rc, tree[rt1].rc, m+1, r
    struct node{
        int lc, rc, w;
        node(){}
    } tree[N * 20];
    int root[N], cnt;
    void build(){
        root[0] = cnt = 0;
        memset(tree, 0, sizeof(tree));
    }

    void add(int pos, int val, int &rt, int rt1, int l, int r){
        tree[rt = ++cnt] = tree[rt1];
        tree[rt].w += val;
        if (l == r) return;
        int m = (l + r) >> 1;
        if (pos <= m) add(pos, val, lson);
        else add(pos, val, rson);
    }
	//单点查询
    int query(int k, int rt, int rt1, int l, int r){
        if (l == r) return l;
        int lsize = sum(tree[rt1].lc) - sum(tree[rt].lc);
        int m = (l + r) >> 1;
        if (lsize >= k) return query(k, lson);
        else return query(k - lsize, rson);
    }
	//区间查询
    LL query(int L, int R, int rt, int rt1, int l, int r){
        if (L <= l && r <= R) return sum(rt1) - sum(rt);
        if (sum(rt1) == sum(rt)) return 0;
        LL ans = 0;
        int m = (l + r) >> 1;
        if (L <= m) ans += query(L, R, lson);
        if (m <  R) ans += query(L, R, rson);
        return ans;
    }
} T;

int main(){
    //freopen("in.txt","r",stdin);
    int _, l, r, k, n, q;
    for (; ~scanf("%d%d", &n, &q);){
        T.build();
        for (int i = 1; i <= n; i++) {
            scanf("%d", &arr[i]);
            Rank[i] = arr[i];
        }
        sort(Rank + 1, Rank + n+1);//Rank存储原值
        int m = unique(Rank + 1, Rank + n +1) - (Rank + 1);//这个m很重要，WA一天系列
        for (int i = 1; i <= n; i++) {//离散化后的数组，仅仅用来更新
            arr[i] = lower_bound(Rank + 1, Rank + m+1, arr[i]) - Rank;
        }
        for (int i = 1; i <= n; i++){
            T.add(arr[i], 1, T.root[i], T.root[i-1], 1, m);//填m别填n
        }
        for (; q--;){
            scanf("%d%d%d", &l, &r, &k);
            int pos = T.query(k, T.root[l-1], T.root[r], 1, m);
            printf("%d\n", Rank[pos]);
        }
    }
    return 0;
}

kd-Tree

解决空间最短距离的利器

//Poj2648
#include 
#include 
#include 
#include 
#include 
using namespace std;
#define Min(a, b) ((a)<(b)?(a):(b))
#define Max(a, b) ((a)>(b)?(a):(b))
#define Abs(x) ((x)>0?(x):-(x))
#define N 500010
#define M 500010
int n, m;

struct Point {
    int x, y;
    Point(int _x = 0, int _y = 0):x(_x),y(_y){}
    void set(int _, int __) { x = _, y = __;}
}P[N + M];
int Dis(const Point &A, const Point &B) {
    return Abs(A.x - B.x) + Abs(A.y - B.y);
}

bool sign;
inline bool cmp(const Point &A, const Point &B) {
    if (sign) return A.x < B.x || (A.x == B.x && A.y < B.y);
    else return A.y < B.y || (A.y == B.y && A.x < B.x);
}

struct Node {
    Node *l, *r;
    int x[2], y[2];
    Point p;

    void SetP(const Point &P) {
        p = P;
        x[0] = x[1] = P.x;
        y[0] = y[1] = P.y;
    }
    int Dis(const Point &p) const {
        int res = 0;
        if (p.x < x[0] || p.x > x[1])
            res += (p.x < x[0]) ? x[0] - p.x : p.x - x[1];
        if (p.y < y[0] || p.y > y[1])
            res += (p.y < y[0]) ? y[0] - p.y : p.y - y[1];
        return res;
    }
    void up(Node *B) {
        x[0] = Min(x[0], B->x[0]);
        x[1] = Max(x[1], B->x[1]);
        y[0] = Min(y[0], B->y[0]);
        y[1] = Max(y[1], B->y[1]);
    }
} mem[N + M], *C = mem, Tnull, *null = &Tnull;

Node *Build(int tl, int tr, bool d) {
    if (tl > tr) return null;
    int mid = (tl + tr) >> 1;
    sign = d;
    std::nth_element(P + tl + 1, P + mid + 1, P + tr + 1, cmp);
    Node *q = C++;
    q->SetP(P[mid]);
    q->l = Build(tl, mid - 1, d ^ 1);
    q->r = Build(mid + 1, tr, d ^ 1);
    if (q->l != null) q->up(q->l);
    if (q->r != null) q->up(q->r);
    return q;
}

#define INF 0x3f3f3f3f
int res;
void Ask(Node *q, const Point &p) {
    res = Min(res, Dis(q->p, p));
    int DisL = q->l != null ? q->l->Dis(p) : INF;
    int DisR = q->r != null ? q->r->Dis(p) : INF;
    if (DisL < DisR) {
        if (q->l != null) Ask(q->l, p);
        if (DisR < res && q->r != null) Ask(q->r, p);
    } else {
        if (q->r != null) Ask(q->r, p);
        if (DisL < res && q->l != null) Ask(q->l, p);
    }
}

void Insert(Node *root, const Point &p) {
    Node *q = C++;
    q->l = q->r = null;
    q->SetP(p);
    sign = 0;
    while(1) {
        root->up(q);
        if (cmp(q->p, root->p)) {
            if (root->l == null) {
                root->l = q;
                break;
            }
            else root = root->l;
        }
        else {
            if (root->r == null) {
                root->r = q;
                break;
            }
            else root = root->r;
        }
        sign ^= 1;
    }
}

int main() {
    scanf("%d%d", &n, &m);
    register int i;
    int ope, x, y;
    for(i = 1; i <= n; ++i) {
        scanf("%d%d", &x, &y);
        P[i] = Point(x, y);
    }
    Node* root = Build(1, n, 0);
    while(m--) {
        scanf("%d%d%d", &ope, &x, &y);
        if (ope == 1) Insert(root, Point(x, y));
        else {
            res = INF;
            Ask(root, Point(x, y));
            printf("%d\n", res);
        }
    }
    return 0;
}

Treap

#include
#include
#include
#include
using namespace std;
struct Node{
    Node *ch[2];
    int r, v, s;//s表示节点数

    Node(int v):v(v){
        ch[0]=ch[1]=NULL;
        r = rand();//在cstdlib头声明
        s = 1;
    }

    int cmp(int x){
        if (x == v) return -1;
        return xs;
        if(ch[1]!=NULL) s+=ch[1]->s;
    }
}; //root全局使用的话可以在这里跟上*root

void rotate(Node* &o,int d){
    Node *k=o->ch[d^1];
    o->ch[d^1]=k->ch[d];
    k->ch[d]=o;
    o->maintain();
    k->maintain();
    o=k;
}
void insert(Node* &o,int x){//o子树中事先不存在x
    if(o==NULL) o=new Node(x);
    else{
        //如这里改成int d=o->cmp(x);
        //就不可以插入相同的值，因为d可能为-1
        int d=x<(o->v)?0:1;
        insert(o->ch[d],x);
        if(o->ch[d]->r > o->r)
            rotate(o,d^1);
    }
    o->maintain();
}
void remove(Node* &o,int x){
    if (o==NULL) return ;//空时返回
    int d=o->cmp(x);
    if (d == -1){
        Node *u=o;
        if(o->ch[0] && o->ch[1]){
            int d2=(o->ch[0]->r < o->ch[1]->r)?0:1;
            rotate(o,d2);
            remove(o->ch[d2],x);
        }else{
            if(o->ch[0]==NULL) o=o->ch[1];
            else o=o->ch[0];
            delete u;//这个要放里面
        }
    }
    else remove(o->ch[d],x);
    if(o) o->maintain();//之前o存在,但是删除节点后o可能就是空NULL了,所以需要先判断o是否为空
}
//返回关键字从小到大排序时的第k个值
//若返回第K大的值，只需要把ch[0]和ch[1]全互换就可以了
int kth(Node* o,int k){
    assert(o && k>=1 && k<=o->s);//保证输入合法,根据实际问题返回
    int s=(o->ch[0]==NULL)?0:o->ch[0]->s;
    if(k==s+1) return o->v;
    else if(k<=s) return kth(o->ch[0],k);
    else return kth(o->ch[1],k-s-1);
}
//返回值x在树中的排名,就算x不在o树中也能返回排名
//返回值范围在[1,o->s+1]范围内
int rank(Node* o,int x){
    if(o==NULL) return 1;//未找到x;
    int num= o->ch[0]==NULL ? 0:o->ch[0]->s;
    if(x==o->v) return num+1;
    else if(x < o->v) return rank(o->ch[0],x);
    else return rank(o->ch[1],x)+num+1;
}

int main(){
    int n=0, v;
    while(scanf("%d",&n)==1 && n){
        Node *root=NULL; //初始化为NULL
        for(int i=0; i

分块

分块入门 1

给出一个长为n的数列，以及n个操作，操作涉及区间加法，单点查值。

int n, blo;
int v[50005],bl[50005],atag[50005];
void add(int a, int b, int c){
    for(int i=a;i<=min(bl[a]*blo,b);i++) v[i]+=c;
    if(bl[a]!=bl[b])
        for(int i=(bl[b]-1)*blo+1;i<=b;i++) v[i]+=c;
    for(int i=bl[a]+1;i<=bl[b]-1;i++) atag[i]+=c;
}
int main(){
    n=read(); blo=sqrt(n);
    for(int i=1;i<=n;i++)v[i]=read();
    for(int i=1;i<=n;i++)bl[i]=(i-1)/blo+1;
    for(int i=1;i<=n;i++){
        int f=read(),a=read(),b=read(),c=read();
        if(f==0)add(a,b,c);
        if(f==1)printf("%d\n",v[b]+atag[bl[b]]);
    }
    return 0;
}

分块入门 2

给出一个长为n的数列，以及n个操作，操作涉及区间加法，询问区间内小于某个值x的元素个数。

int n,blo;
int v[50005], bl[50005], atag[50005];
vectorve[505];
void reset(int x){
    ve[x].clear();
    for(int i=(x-1)*blo+1;i<=min(x*blo,n);i++)
        ve[x].push_back(v[i]);
    sort(ve[x].begin(),ve[x].end());
}
void add(int a,int b,int c){
    for(int i=a;i<=min(bl[a]*blo,b);i++)
        v[i]+=c;
    reset(bl[a]);
    if(bl[a]!=bl[b]){
        for(int i=(bl[b]-1)*blo+1;i<=b;i++)v[i]+=c;
        reset(bl[b]);
    }
    for(int i=bl[a]+1;i<=bl[b]-1;i++)
        atag[i]+=c;
}
int query(int a,int b,int c){
    int ans=0;
    for(int i=a;i<=min(bl[a]*blo,b);i++)
        if(v[i]+atag[bl[a]]

分块入门 3

给出一个长为n的数列，以及n个操作，操作涉及区间加法，询问区间内小于某个值x的前驱（比其小的最大元素）。

int n,blo;
int v[100005],bl[100005],atag[100005];
setst[105];
void add(int a,int b,int c){
    for(int i=a;i<=min(bl[a]*blo,b);i++){
        st[bl[a]].erase(v[i]);
        v[i] += c;
        st[bl[a]].insert(v[i]);
    }
    if(bl[a]!=bl[b]){
        for(int i=(bl[b]-1)*blo+1;i<=b;i++){
            st[bl[b]].erase(v[i]);
            v[i] += c;
            st[bl[b]].insert(v[i]);
        }
    }
    for(int i=bl[a]+1;i<=bl[b]-1;i++)
        atag[i]+=c;
}
int query(int a,int b,int c){
    int ans=-1;
    for(int i=a;i<=min(bl[a]*blo,b);i++){
        int val=v[i]+atag[bl[a]];
        if(val::iterator it=st[i].lower_bound(x);
        if(it==st[i].begin())continue;
        --it;
        ans=max(ans,*it+atag[i]);
    }
    return ans;
}
int main(){
    n=read();blo=1000;
    for(int i=1;i<=n;i++)v[i]=read();
    for(int i=1;i<=n;i++){
        bl[i]=(i-1)/blo+1;
        st[bl[i]].insert(v[i]);
    }
    for(int i=1;i<=n;i++){
        int f=read(),a=read(),b=read(),c=read();
        if(f==0)add(a,b,c);
        if(f==1)printf("%d\n",query(a,b,c));
    }
    return 0;
}

左偏树

#include 
#include 
#include 
#include 
using namespace std;
const int MAXN = 1e5 + 5;
struct node{
    int l,r,dis,key;
} tree[MAXN];
int far[MAXN];
int Find(int x) {
    if(far[x] == x) return x;
    return far[x] = Find(far[x]);
}

int merge(int a,int b){
    if(!a) return b;
    if(!b) return a;
    if(tree[a].key < tree[b].key) swap(a, b);//大堆
    tree[a].r = merge(tree[a].r,b);
    far[tree[a].r] = a;//并查
    if(tree[tree[a].l].dis < tree[tree[a].r].dis) swap(tree[a].l,tree[a].r);
    if(tree[a].r)tree[a].dis = tree[tree[a].r].dis + 1;
    else tree[a].dis = 0;
    return a;
}

int pop(int a){
    int l = tree[a].l;
    int r = tree[a].r;
    far[l] = l;//因为要暂时删掉根，所以左右子树先作为根
    far[r] = r;
    tree[a].l = tree[a].r = tree[a].dis = 0;
    return merge(l,r);
}

int main(){
    int N, M;
    while(cin >> N){
        for(int i = 1; i <= N; i++){
            int x;
            far[i] = i;
            scanf("%d", &x);
            tree[i].key = x;
            tree[i].l = tree[i].r = tree[i].dis = 0;
        }
        cin >> M;
        while(M--) {
            int x, y;
            scanf("%d%d", &x, &y);
            x = Find(x);
            y = Find(y);
            if(x == y) {
                printf("-1\n");
            } else {
                int ra = pop(x);
                tree[x].key /= 2;
                ra = merge(ra, x);
                int rb = pop(y);
                tree[y].key /= 2;
                rb = merge(rb, y);
                x = merge(ra, rb);
                printf("%d\n", tree[x].key);
            }
        }
    }
    return 0;
}

Splay

#include
#include
using namespace std;
struct Node{
    int key;//size
    Node *l,*r,*f;//left,right,father
};
class SplayTree{
public:
    void Init(){rt=NULL;}
    void Zag(Node *x){//left rotate
        Node *y=x->f;//y is the father of x
        y->r = x->l;
        if (x->l)x->l->f = y;//if x has left child
        x->f =y->f;
        if (y->f){//y is not root
            if (y==y->f->l)y->f->l=x;//y if left child
            else y->f->r=x;//y is right child
        }
        y->f=x; x->l=y;
    }
    void Zig(Node *x){//right rotate
        Node *y=x->f;//y is the father of x
        y->l = x->r;
        if (x->r)x->r->f=y;
        x->f = y->f;
        if (y->f){
            if (y==y->f->l)y->f->l=x;
            else y->f->r=x;
        }
        y->f=x;
        x->r=y;
    }
    void Splay(Node *x){
        while (x->f){
            Node *p=x->f;
            if (!p->f){
                if (x==p->l)Zig(x);
                else Zag(x);
            }else if (x==p->l){
                if (p==p->f->l){Zig(p);Zig(x);}
                else {Zig(x);Zag(x);}
            }else {//x==p->r
                if (p==p->f->r){Zag(p);Zag(x);}
                else {Zag(x);Zig(x);}
            }
        }
        rt=x;
    }
    Node *Find(int x){
        Node *T=rt;
        while (T){
            if (T->key==x){Splay(T);return T;}
            else if (xkey)T=T->l;
            else T=T->r;
        }
        return T;
    }
    void Insert(int x){
        Node *T=rt,*fa=NULL;
        while (T){
            fa=T;
            if (xkey)T=T->l;
            else if(x>T->key)T=T->r;
            else return ;//two the same keys
        }
        T=(Node*)malloc(sizeof(Node));
        T->key=x;
        T->l=T->r=NULL;
        T->f=fa;
        if (fa){
            if (fa->key>x)fa->l=T;
            else fa->r=T;
        }
        Splay(T);
    }
    void Delete(int x){
        Node *T=Find(x);
        if (NULL==T)return ;//error
        rt=Join(T->l,T->r);
    }
    Node *Maxnum(Node *t){
        Node *T=t;
        while (T->r)T=T->r;
        Splay(T);
        return T;
    }
    Node *Minnum(Node *t){
        Node *T=t;
        while (T->l)T=T->l;
        Splay(T);
        return T;
    }
    Node *Last(int x){
        Node *T=Find(x);
        T=T->l;
        return (Maxnum(T));
    }
    Node *Next(int x){
        Node *T=Find(x);
        T=T->r;
        return (Minnum(T));
    }
    Node *Join(Node *t1,Node *t2){
        if (NULL==t1)return t2;
        if (NULL==t2)return t1;
        Node *T=Maxnum(t1);
        T->l=t2;
        return T;
    }
    void Split(int x,Node *&t1,Node *&t2){
        Node *T=Find(x);
        t1=T->l; t2=T->r;
    }
    void Inorder(Node *T){
        if (NULL==T)return ;
        Inorder(T->l);
        printf("%d->",T->key);
        Inorder(T->r);
    }
    void _Delete(){Delete(rt);}
    void Delete(Node *T){
        if (NULL==T)return ;
        Delete(T->l);
        Delete(T->r);
        free(T);
    }
private:
    Node *rt;//root
};

AVL树

//codevs1285 莯ʕѸ˹
//by cww97
#include
#include
#include
#define INF 0xfffffff
#define BASE 1000000
using namespace std;
int ans=0;
struct Node{
    int x,bf,h;//bf=balance factor,h=height
    Node *l,*r;
};

class AVLTree{
public:
    void Init() { rt = NULL; }
    int H(Node *T){return (T==NULL)?0:T->h;}
    int BF(Node *l,Node *r){//get balance factor
        if (NULL==l && NULL==r) return 0;
        else if (NULL == l) return -r->h;
        else if (NULL == r) return  l->h;
        return l->h - r->h;
    }

    Node *Lrorate(Node *a){//left rorate
        Node *b;
        b=a->r;
        a->r=b->l;
        b->l=a;
        a->h=max(H(a->l),H(a->r)) + 1;
        b->h=max(H(b->l),H(b->r)) + 1;
        a->bf=BF(a->l,a->r);
        b->bf=BF(b->l,b->r);
        return b;
    }
    Node *Rrorate(Node *a){//right rorate
        Node *b;
        b=a->l;
        a->l=b->r;
        b->r=a;
        a->h=max(H(a->l),H(a->r)) + 1;
        b->h=max(H(b->l),H(b->r)) + 1;
        a->bf=BF(a->l,a->r);
        b->bf=BF(b->l,b->r);
        return b;
    }
    Node *LRrorate(Node *a){//left then right
        a->l = Lrorate(a->l);
        Node *c;
        c=Rrorate(a);
        return c;
    }
    Node *RLrorate(Node *a){//right then left
        a->r=Rrorate(a->r);
        Node *c;
        c=Lrorate(a);
        return c;
    }

    void Insert(int x){_Insert(rt,x);}
    void _Insert (Node *&T,int x){
        if (NULL==T){
            T=(Node*)malloc(sizeof(Node));
            T->x=x;
            T->bf=0;T->h=1;
            T->l=T->r=NULL;
            return ;
        }
        if      (x < T->x) _Insert(T->l,x);
        else if (x > T->x) _Insert(T->r,x);
        else return ; //error :the same y

        T->h=max(H(T->l),H(T->r))+1;//maintain
        T->bf=BF(T->l,T->r);

        if (T->bf > 1 || T->bf < -1){//not balanced
            if      (T->bf > 0 && T->l->bf > 0)T=Rrorate(T);
            else if (T->bf < 0 && T->r->bf < 0)T=Lrorate(T);
            else if (T->bf > 0 && T->l->bf < 0)T=LRrorate(T);
            else if (T->bf < 0 && T->r->bf > 0)T=RLrorate(T);
        }
    }

    void GetPet(int x){//get pet or person
        if (NULL==rt){return ;}
        int small=0,large=INF;
        //printf("x=%d\n",x);
        int flag;
        if (Find(rt,x,small,large)){
            printf("find %d\n",x);
            _Delete(rt,x);
        }else if (small==0)flag=1;
        else if (large==INF)flag=0;
        else if (large-xx)return 1;
        if (xx){
            large=min(large,T->x);
            return Find(T->l,x,small,large);
        }else{
            small=max(small,T->x);
            return Find(T->r,x,small,large);
        }
    }
    void _Delete(Node *&T,int x){
        if (NULL==T)return ;
        if       (x < T->x){//y at left
            _Delete(T->l,x);
            T->bf=BF(T->l,T->r);
            if (T->bf<-1){
                if (1==T->r->bf)T=RLrorate(T);
                else T=Lrorate(T);//bf==0 or -1
            }
        }else if (x > T->x){//y at right
            _Delete(T->r,x);
            T->bf=BF(T->l,T->r);
            if (T->bf>1){
                if (-1==T->l->bf)T=LRrorate(T);
                else T=Rrorate(T);//bf==0 or 1
            }
        }else {//here is x
            if (T->l&&T->r){//left &&right
                Node *t=T->l;
                while (t->r)t=t->r;
                T->x=t->x;
                _Delete(T->l,t->x);
                T->bf=BF(T->l,T->r);
                if (T->bf<-1){
                    if (1==T->r->bf)T=RLrorate(T);
                    else T=Lrorate(T);//bf==0 or -1
                }
            }else {//left || right
                Node *t=T;
                if (T->l)T=T->l;
                else if(T->r)T=T->r;
                else {free(T);T=NULL;}
                if (T)free(t);
            }
        }
    }

    //Debug,you will not need it at this problem
    void show(){InOrder(rt);puts("EndShow");}
    void InOrder(Node *T){//print l rt r
        if (NULL==T)return ;
        InOrder(T->l);
        printf("%d ",T->x);
        InOrder(T->r);
    }
    void Free(){FreeTree(rt);}
    void FreeTree(Node *T){
        if (NULL==T)return ;
        FreeTree(T->l);
        FreeTree(T->r);
        free(T);
    }

private:
    Node *rt;//root
};

int main(){
    freopen("fuck.in","r",stdin);
    int n,x,op,a=0,b=0;
    scanf("%d",&n);
    AVLTree T; T.Init();
    for (;n--;){
        scanf("%d%d",&op,&x);
        //if pets>people put pets into the tree
        //else put people into the tree
        if (op==0){//come a pet
            a++;
            if (a>b)T.Insert(x);//more pet
            else T.GetPet(x);//more people
        }else{//come a person
            b++;
            if (a

图论

图论通用模板

闭眼可敲，改编自刘汝佳的图论板，不过改用了前向星建图，防止卡常
本册大部分图论算法都基于本模板

struct graph{
    struct Edge{
        int from, to, cost, nxt;
        Edge(){}
        Edge(int x, int y, int z, int w):from(x), to(y), cost(z), nxt(w){}
    } edges[M];
    int n, head[N], E;

    inline void init(int _n){
        n = _n; E = 0;
        for (int i = 0; i <= n; i++) head[i] = -1;
    }

    inline void addEdge(int f, int t, int c){
        edges[E] = Edge(f, t, c, head[f]);
        head[f] = E++;
    }
} g;

最小生成树（prim）

hdu1102

#include
#include
#include
using namespace std;
const int N=107;
int n,g[N][N];

int prim(){
    int minw[N];//MinWeight
    bool used[N];
    memset(used,0,sizeof(used));
    memset(minw,0x7f,sizeof(minw));
    minw[1]=0;
    int sum=0;
    while (1){
        int v=-1;
        for (int i=1;i<=n;i++){
            if (!used[i]&&(v==-1||minw[i]

次小生成树

#include
#include
#include
#include
#include
using namespace std;
#define N 510
int map[N][N], lowcost[N], pre[N], max1[N][N], stack[N];
bool visit[N];
int n, m, sum;
  
void prim(){ //默认1在MST中
    int temp, k;
    int top; //保存最小生成树的结点
  
    memset(visit, false, sizeof(visit)); //初始化
    visit[1] = true;  
    sum = top = 0;  
    for(int i = 1; i <= n; ++i){  
        pre[i] = 1;
        lowcost[i] = map[1][i];
    }  
    lowcost[1] = 0;  
    stack[top++] = 1; //保存MST的结点  
  
    for(int i = 1; i <= n; ++i){  
        temp = INT_MAX;  
        for(int j = 1; j <= n; ++j)  
            if(!visit[j] && temp > lowcost[j])  
                temp = lowcost[k = j];  
        if(temp == INT_MAX) break;  
        visit[k] = true;  
        sum += temp;  
        for(int j = 0; j < top; ++j) //新加入点到MST各点路径最大值  
            max1[stack[j]][k] = max1[k][stack[j]] = max(max1[stack[j]][pre[k]], temp);  
        stack[top++] = k; //保存MST的结点  
  
        for(int j = 1; j <= n; ++j) //更新  
            if(!visit[j] && lowcost[j] > map[k][j]){  
                lowcost[j] = map[k][j];  
                pre[j] = k; //记录直接前驱  
            }  
    }  
}  
  
int main(){  
    int ncase, start, end, cost, minn;  
    scanf("%d", &ncase);  
    while(ncase--)  {  
        for(int i = 1; i < N; ++i) //初始化不为0,1必须用循环。。。。  
            for(int j = 1; j < N; ++j){  
                map[i][j] = INT_MAX;  
                max1[i][j] = 0;  
            }  
        scanf("%d%d", &n, &m);  
        for(int i = 1; i <= m; ++i){  
            scanf("%d%d%d", &start, &end, &cost);  
            //if(cost < map[start][end])(POJ竟然出现重边的时候不选择最小的~~~)  
            map[start][end] = map[end][start] = cost;  
        }  
        prim();
        minn = INT_MAX;
        for(int i = 1; i <= n; ++i)  
            for(int j = 1; j <= n; ++j)  
                if(i != j && i != pre[j] && j != pre[i]) //枚举MST以外的边  
                    minn = min(minn, map[i][j] - max1[i][j]); //求出{MST外加入边-MST环上权值最大边}最小值  
        if(minn != 0) printf("No\n");  
        else printf("Yes\n");  
    }  
    return 0;  
} 

最短路（SPFA）

bool inq[N];
int dist[N];
inline int spfa(const int &s, const int &t){
    queue  Q;
    memset(inq, 0, sizeof(inq));
    memset(dist, INF, sizeof(dist));
    dist[s]=0; inq[s]=1;
    for (Q.push(s); !Q.empty();){
        int u = Q.front(); Q.pop(); inq[u]= 0;
        for (int i = head[u]; ~i; i = edges[i].nxt){
            Edge &e = edges[i];
            if (dist[u] + e.cost < dist[e.to]){
                dist[e.to] = dist[u] + e.cost;
                if (!inq[e.to]){
                    Q.push(e.to);
                    inq[e.to] = 1;
                }
            }
        }
    }
    return dist[t];
}

找负环

bool find_negative_loop() {
	memset(d, 0, sizeof(d));
	for(int i = 0; i < V; i++) {
		for(int j = 0; j < E; j++) {
			edge e = es[j];
			if(d[e.to] > d[e.form] + e.cost) {
				d[e.to] = d[e.from] + e.cost;
				if(i == V - 1) return true;
			}
		}
	}
	return false;
}

最短路Dijkstra同时求解次短路

#include 
#include 
#include 
#include 
using namespace std;
typedef long long LL;
typedef pair P;
const int INF = 0x3f3f3f3f3f3f3f3f;
const int N = 2e5 + 7;

struct Edge{
    int to;
    LL cost;
    Edge(int tv = 0, LL tc = 0):to(tv), cost(tc){}
};
vector G[N];
int n, m;
LL dist[N];     //最短距离
LL dist2[N];    //次短距离

LL Dijkstra(){
    memset(dist, INF, sizeof(dist));
    memset(dist2, INF, sizeof(dist2));
    //从小到大的优先队列
    //使用pair而不用edge结构体
    //是因为这样我们不需要重载运算符
    //pair是以first为主关键字进行排序
    priority_queue, greater
 > Q;
    //初始化源点信息
    dist[1] = 0;
    Q.push(P(0, 1));
    //同时求解最短路和次短路
    for(; !Q.empty();){
        P p = Q.top(); Q.pop();
        //first为s->to的距离，second为edge结构体的to
        int v = p.second;
        LL d = p.first;
        //当取出的值不是当前最短距离或次短距离，就舍弃他
        if (dist2[v] < d) continue;
        for (int i = 0; i < G[v].size(); i++){
            Edge &e = G[v][i];
            LL d2 = d + e.cost;
            if (dist[e.to] > d2){
                swap(dist[e.to], d2);
                Q.push(P(dist[e.to], e.to));
            }
            //printf("dist2[%d] = %d, d2 = %d\n", e.to, dist2[e.to], d2);
            if (dist2[e.to] > d2 && dist[v] < d2){
                dist2[e.to] = d2;
                Q.push(P(dist2[e.to], e.to));
            }
        }
    }
    return dist2[n];
}

上面的次短路是假的，这是真的

今天重新写用的是SPFA。正反跑两次SPFA，然后枚举每一条边，如果起点到一个端点的最短路+另一个端点到终点的最短路+长度 ≠ 最短路，则和答案比较，保存最小值。还是很好理解的:D

#include 
#include 
#include 
#include 
#include 
using namespace std;
const int MAXR = 100000 + 50;
const int MAXN = 5000 + 50;
const int INF = 0x7fffffff;
struct edge{
    int to, len;
    edge(int x, int y): to(x), len(y) {}
};
vector E[MAXN];
int n,r,dis[MAXN],inque[MAXN],dis1[MAXN],dis2[MAXN];
int u[MAXR],v[MAXR],w[MAXR];

void addedge(int u,int v,int w){
    E[u].push_back(edge(v,w));
    E[v].push_back(edge(u,w));
}

void spfa(int S,int T){
    for (int i=1; i<=n; i++) inque[i]=0,dis[i]=INF;
    queue que;
    que.push(S);
    inque[S]=1;
    dis[S]=0;
    for (;!que.empty();){
        int head=que.front();
        que.pop();
        inque[head]=0;
        for (int i=0; i

多源最短路(Floyed)

inline void floyed(){
    for (int k=1;k<=n;k++)
      for (int i=1;i<=n;i++)if (i!=k)
        for (int j=1;j<=n;j++)if (j!=i&&j!=k)
          d[i][j]=min(d[i][j], d[i][k]+d[k][j]);
}

匈牙利

二分图匹配（匈牙利算法的DFS实现）
INIT：g[][]两边定点划分的情况
CALL:res=hungary();输出最大匹配数
优点：适于稠密图，DFS找增广路快，实现简洁易于理解
时间复杂度:O(VE);

#include
using namespace std;
const int N = 200 + 7;
const int INF = 0x3f3f3f3f;

struct Hungary{
    vector  G[N];
    bool used[N];// main里面记得memset
    int girl[N], n;
    inline void init(int _n){
        n = _n;
        for (int i = 0; i <= n; i++) G[i].clear();
    }
    inline void addEdge(const int &u, const int &v){
        G[u].push_back(v);
        //printf("addEdge %d %d\n", u, v);
    }

    bool Find(int x){
        for (int i = 0; i < G[x].size(); i++){    //扫描每个妹子
            int j = G[x][i];
            if (used[j]) continue;
            // 如果有暧昧并且还没有标记过
            // (这里标记的意思是这次查找曾试图改变过该妹子的归属问题，
            // 是没有成功，所以就不用瞎费工夫了）
            used[j] = 1;
            if (girl[j] == -1 || Find(girl[j])) {
                //名花无主或者能腾出个位置来，这里使用递归
                girl[j] = x;
                return true;
            }
        }
        return false;
    }

    inline int hungary(const int &n, const int &m){
        int all = 0;
        memset(girl, -1, sizeof girl);
        for (int i = 0; i < n; i++) {
            memset(used, 0, sizeof(used)); //这个在每一步中清空
            if (Find(i)) all += 1;
        }
        //for (int i = 0; i < m; i++) printf("girl[%d] = %d\n", i, girl[i]);
        //printf("all = %d\n", all);
        return all;
    }
} hg;

KM算法

待补，最大权二分匹配

最大权二分匹配问题就是给二分图的每条边一个权值，选择若干不相交的边，得到的总权值最大。解决这个问题可以用KM算法。理解KM算法需要首先理解“可行顶标”的概念。可行顶标是指关于二分图两边的每个点的一个值lx[i]或ly[j]，保证对于每条边w[i][j]都有lx[i]+ly[j]-w[i][j]>=0。如果所有满足lx[i]+ly[j]==w[i][j]的边组成的导出子图中存在一个完美匹配，那么这个完美匹配肯定就是原图中的最大权匹配。理由很简单：这个匹配的权值之和恰等于所有顶标的和，由于上面的那个不等式，另外的任何匹配方案的权值和都不会大于所有顶标的和。

但问题是，对于当前的顶标的导出子图并不一定存在完美匹配。这时，可以用某种方法对顶标进行调整。调整的方法是：根据最后一次不成功的寻找交错路的DFS，取所有i被访问到而j没被访问到的边(i,j)的lx[i]+ly[j]-w[i][j]的最小值d。将交错树中的所有左端点的顶标减小d，右端点的顶标增加d。经过这样的调整以后：原本在导出子图里面的边，两边的顶标都变了，不等式的等号仍然成立，仍然在导出子图里面；原本不在导出子图里面的边，它的左端点的顶标减小了，右端点的顶标没有变，而且由于d的定义，不等式仍然成立，所以他就可能进入了导出子图里。

初始时随便指定一个可行顶标，比如说lx[i]=max{w[i][j]|j是右边的点}，ly[i]=0。然后对每个顶点进行类似Hungary算法的find过程，如果某次find没有成功，则按照这次find访问到的点对可行顶标进行上述调整。这样就可以逐步找到完美匹配了。

值得注意的一点是，按照上述d的定义去求d的话需要O(N^{2)的时间，因为d需要被求O(N}2)次，这就成了算法的瓶颈。可以这样优化：设slack[j]表示右边的点j的所有不在导出子图的边对应的lx[i]+ly[j]-w[i][j]的最小值，在find过程中，若某条边不在导出子图中就用它对相应的slack值进行更新。然后求d只要用O(N)的时间找到slack中的最小值就可以了。

如果是求最小权匹配，只需要把那个不等式反一下就行了。算法需要作出的改变是：lx的初值为所有临界边中的最小值，find中t反号。

#define M 505  
#define inf 0x3fffffff  
bool sx[M], sy[M];  
int match[M], w[M][M], n, m, d, lx[M], ly[M];  
//n：左集元素个数； m：右集元素个数  
void init ()  {  
    memset (w, 0, sizeof(w));    //不一定要，求最小值一般要初始化为负无穷！  
}  
  
bool dfs (int u)  {  
    int v; sx[u] = true;  
    for (v = 0; v < m; v++)  {  
        if (!sy[v] && lx[u]+ly[v]==w[u][v])  {  
            sy[v] = true;  
            if (match[v] == -1 || dfs (match[v]))  {  
                match[v] = u;  
                return true;  
            }  
        }  
    }  
    return false;  
}  
  
int KM ()  {  
    int i, j, k, sum = 0;  
    memset (ly, 0, sizeof(ly));  
    for (i = 0; i < n; i++)  {  
        lx[i] = -inf;  
        for (j = 0; j < m; j++)  
            if (lx[i] < w[i][j]) lx[i] = w[i][j];  
    }  
    memset (match, -1, sizeof(match));  
    for (i = 0; i < n; i++)  {  
        while (1)  {  
            memset (sx, false, sizeof(sx));  
            memset (sy, false, sizeof(sy));  
            if (dfs (i))  break;  
            d = inf;  
            for (j = 0; j < n; j++)  if (sx[j])  
                for (k = 0; k < m; k++)  if (!sy[k])  
                    d = min (d, lx[j]+ly[k]-w[j][k]);  
            if (d == inf) return -1; //找不到完美匹配
            for (j = 0; j < n; j++) if (sx[j]) lx[j] -= d;  
            for (j = 0; j < m; j++) if (sy[j]) ly[j] += d;  
        }  
    }  
    for (i = 0; i < m; i++) if (match[i] > -1) 
        sum += w[match[i]][i];  
    return sum;  
}  

欧拉回路dfs

stackS;
bool vis[N]; //use when dfs
inline void dfs(int x){//get EulerCircle
    Edge e;
    for (int i=head[x];i!=-1;i=e.nxt){
        e = edges[i];
        if (vis[i])continue;
        vis[i] = 1;
        dfs(e.to);
        S.push(x);
    }
}
inline void getEulerCircle(){
    while (!S.empty())S.pop();
    memset(vis,0,sizeof(vis));
    dfs(1);
    for (;!S.empty();S.pop())
        printf("%d ",S.top());
    puts("1");
}

混合图欧拉回路

解析见紫书376

ATTENTION:需要注意的是，网络流里是有反向边的，dinic跑完之后反向边不要添加到新图里面了
加到Dinic里面

    inline void buildEuler(int n){
        for (int i=1;i<=n;i++){
            for (int nxt,j=head[i];j!=-1;j=nxt){
                Edge &e = edges[j]; nxt = e.nxt;
                if (e.to==s||e.to==t) continue ;
                if (!e.cap)continue;
                if (e.flow==e.cap)gg.AddEdge(e.to,e.from);
                else gg.AddEdge(e.from, e.to);
            }
        }
    }

main哇哦

int d[N];//degree = out - in
bool work(int n){
    int flow = 0;
    for (int i=1;i<=n;i++){
        if (d[1]&1)return 0;
        if (d[i]>0){
            g.AddEdge(g.s,i,d[i]>>1);
            flow += d[i]>>1;
        }else if (d[i]<0)
            g.AddEdge(i,g.t,-(d[i]>>1));
    }
    if (flow != g.maxFlow()) return 0;
    return 1;
}

int main(){
    //freopen("in.txt","r",stdin);
    int T,x,y,n,m;
    scanf("%d",&T);
    for (char ch;T--;){
        scanf("%d%d",&n,&m);
        g.Init(n,0,n+1);
        gg.Init(n);
        memset(d,0,sizeof(d));
        for (int i=1;i<=m;i++){
            scanf("%d%d %c\n",&x,&y,&ch);
            if (ch=='D') gg.AddEdge(x,y);
            else g.AddEdge(x,y,1);
            d[x]++;d[y]--;//Degree
        }
        if (!work(n))puts("No euler circuit exist");
        else {
            g.buildEuler(n);
            gg.getEulerCircle();
        }
        if (T)puts("");
    }
    return 0;
}

最大流（Dinic）

#include
#include
#include
#include
#include
#include
using namespace std;
typedef long long LL;
const int INF=0x3f3f3f3f;
const int N = 9999;

struct Dinic{
    struct Edge{
        int from,to,cap,flow,nxt;
        Edge(){}
        Edge(int u,int v,int c,int f,int n):
            from(u),to(v),cap(c),flow(f),nxt(n){}
    }edges[N];
    int n, s, t, E, head[N];
    bool vis[N]; //use when bfs
    int d[N],cur[N];//dist,now edge,use in dfs
    inline void AddEdge(int f,int t,int c){
        edges[++E] = Edge(f,t,c,0,head[f]);
        head[f] = E;
        edges[++E] = Edge(t,f,0,0,head[t]);
        head[t] = E;
    }
    inline void Init(int n,int s,int t){
        this -> n = n ; E = -1;
        this -> s = s ; head[s] = -1;
        this -> t = t ; head[t] = -1;
        for (int i=0;i<=n;i++) head[i] = -1;
    }

    inline bool BFS(){
        memset(vis,0,sizeof(vis));
        queueQ;
        d[s] = 0; vis[s] = 1;
        for (Q.push(s);!Q.empty();){
            int x = Q.front(); Q.pop();
            for (int nxt,i = head[x];i!=-1;i = nxt){
                Edge &e = edges[i]; nxt = e.nxt;
                if (vis[e.to]||e.cap<=e.flow)continue;
                vis[e.to]=1;
                d[e.to]=d[x]+1;
                Q.push(e.to);
            }
        }
        return vis[t];
    }
    inline int DFS(const int& x,int a){
        if (x==t||a==0){return a;}
        int flow = 0, f, nxt;
        for (int& i=cur[x];i!=-1;i=nxt){
            Edge& e = edges[i]; nxt = e.nxt;
            if (d[x]+1!=d[e.to])continue;
            f = DFS(e.to,min(a,e.cap-e.flow));
            if (f <= 0)continue;
            e.flow += f;
            edges[i^1].flow-=f;  // 反向边
            flow+=f; a-=f;
            if (!a) break;
        }
        return flow;
    }
    inline int maxFlow(){return maxFlow(s,t);}
    inline int maxFlow(int s, int t){
        int flow = 0;
        for (; BFS(); ){
            for (int i = 0;i <= n; i++) cur[i] = head[i];
            flow += DFS(s,INF) ;
        }
        return flow;
    }
} g ;

费用流（SPFA）

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef long long LL;
const int N = 2e4 + 7;
const int INF = 0x3f3f3f3f;
const double EPS = 1e-6;

struct MCMF{
    struct Edge{
        int from, to, cap, flow, nxt;
        LL cost;
        Edge(){}
        Edge(int x,int y,int z,int u,LL v,int n){
            from=x;to=y;cap=z;flow=u;cost=v;nxt=n;
        }
    } edges[N];
    int E, n, head[N];
    int inq[N]; //是否在队列中
    int d[N];   //spfa dist
    int p[N];   //上一条edge的编号
    int a[N];   //可该进量

    inline void init(int _n){
        n = _n; E = 0;
        memset(head, -1, sizeof(head));
    }
    inline void addEdge(int f, int t, int c, LL w){
        edges[E] = Edge(f, t, c, 0, w, head[f]);
        head[f] = E++;
        edges[E] = Edge(t, f, 0, 0,-w, head[t]);
        head[t] = E++;
    }

    bool spfa(int s, int t, int &flow, LL &cost){
        for (int i = 0; i <= n; i++) d[i] = INF;
        memset(inq, 0, sizeof(inq));
        d[s] = 0; inq[s] = 1; p[s] = 0; a[s] = INF;
        queue  Q; Q.push(s);
        for (; !Q.empty();){
            int u = Q.front(); Q.pop(); inq[u] = 0;
            for (int i = head[u]; i != -1; i = edges[i].nxt){
                Edge &e = edges[i];
                if (e.cap<=e.flow || d[e.to]<=d[u]+e.cost) continue;
                d[e.to] = d[u] + e.cost;
                p[e.to] = i;
                a[e.to] = min(a[u], e.cap - e.flow);
                if (!inq[e.to]){Q.push(e.to); inq[e.to] = 1;}
            }
        }
        if (d[t] == INF) return false;
        flow += a[t];
        cost += (LL)d[t] * (LL)a[t];
        for (int u = t; u != s; u = edges[p[u]].from){
            edges[p[u]  ].flow += a[t];
            edges[p[u]^1].flow -= a[t];
        }
        return true;
    }

    //需要保证初始网络中没有负权
    int mcmf(int s, int t, LL &cost){// MinCostMaxFlow
        int flow = 0;
        cost = 0;
        for (; spfa(s, t, flow, cost);){}
        return flow;
    }
} g ;

强连通分量Tarjan + 缩点

hdu5934

#include 
#include 
#include 
#include 
#include 
using namespace std;
typedef long long LL;

struct tarjan{ //复杂度O(N+M)
    const static int MAXN = 1e4 + 7; // 点数
    const static int MAXM = 1e5 + 7; // 边数
    struct Edge{
        int to, nxt;
        Edge(){}
        Edge(int t, int n):to(t), nxt(n){}
    } edge[MAXM];
    int head[MAXN], tot, n;
    int Low[MAXN], DFN[MAXN], Stack[MAXN], Belong[MAXN];//Belong数组的值是1~scc
    int Index, top;
    int scc; // 强连通分量的个数
    int num[MAXN]; // 各个强连通分量包含点的个数，数组编号1~scc //num数组不一定需要，结合实际情况
    bool Instack[MAXN];

    inline void init(int n){
        tot = 0; this->n = n;
        memset(head, -1, sizeof(head));
    }
    inline void addedge(int u, int v){
        edge[tot] = Edge(v, head[u]);
        head[u] = tot++;
    }

    void Tarjan(int u){
        int v;
        Low[u] = DFN[u] = ++Index;
        Stack[top++] = u;
        Instack[u] = true;
        for(int i = head[u]; ~i; i = edge[i].nxt){
            v = edge[i].to;
            if (!DFN[v]){
                Tarjan(v);
                Low[u] = min(Low[u], Low[v]);
            } else if(Instack[v] && Low[u] > DFN[v])
                Low[u] = DFN[v];
        }
        if (Low[u] == DFN[u]){
            scc++;
            do{
                v = Stack[--top];
                Instack[v] = false;
                Belong[v] = scc;
                num[scc]++;
            }while(v != u);
        }
    }

    int indeg[MAXN], outdeg[MAXN];
    inline int solve(int n){
        memset(DFN, 0, sizeof(DFN));
        memset(num, 0, sizeof(num));
        memset(Instack, 0, sizeof(Instack));
        Index = scc = top = 0;
        for(int i = 1; i <= n; i++) if(!DFN[i]) Tarjan(i);
        // for this problem 缩点
        memset(indeg, 0, sizeof(indeg));
        memset(outdeg, 0, sizeof(outdeg));
        if (scc == 1) return 0;
        for(int u = 1; u <= n; u++)
            for(int i = head[u]; i!=-1; i = edge[i].nxt){
                int v = edge[i].to;
                if (Belong[u] != Belong[v]){
                    outdeg[Belong[u]]++;
                    indeg[Belong[v]]++;
                }
            }
        int ans1 = 0, ans2 = 0;
        for(int i = 1; i <= scc; i++){
            if (indeg[i] == 0) ans1++;
            if (outdeg[i] == 0) ans2++;
        }
        // 至少加几条边让整个图变成强连通（即，出度或入度的最大值）
        return max(ans1, ans2);
    }
} g;

倍增LCA + 最大生成树

#include
#include
#include
#include
#include
using namespace std;
const int INF=0x3f3f3f3f;
const int N = 1e5 + 5;
int n,m;

struct gragh{
    struct Edge{
        int from,to,w;
        Edge(){}
        Edge(int x,int y,int z):from(x),to(y),w(z){}
        bool operator < (const Edge& a)const{
            return w < a.w;
        }
    }edges[N],be[N];
    int E,f[N],fa[N][20],di[N][20],dep[N];
    bool vis[N];
    vectorG[N];
    int F(int x){//鼯
        return f[x]==x?x:(f[x]=F(f[x]));
    }

    inline void link(int x,int y,int z){
        edges[++E] = Edge(x,y,z);
        G[x].push_back(E);
    }

    void build(){
        E = 0;
        for (int i = 1;i <= n; i++) G[i].clear();
        int x,y,z;
        for (int i=1;i<=n;i++)f[i]=i;
        for (int i=1;i<=m;i++){
            scanf("%d%d%d",&x,&y,&z);
            be[i]=Edge(x,y,z);
            f[F(x)]=F(y);
        }
    }

    void kruskal(){
        int treenum = 0;//forests
        memset(vis,0,sizeof(vis));
        for (int i=1;i<=n;i++)if (!vis[F(i)]){
            treenum++;vis[F(i)]=1;
        }
        for (int i=1;i<=n;i++)f[i]=i;
        sort(be+1,be+m+1);
        int cnt = 0;
        for (int i=m;i>=1;i--){
            int x = be[i].from;
            int y = be[i].to  ;
            if (F(x)==F(y))continue;
            f[F(x)]=F(y);
            cnt++;
            link(x,y,be[i].w);
            link(y,x,be[i].w);
            if (cnt==n-treenum)break;
        }
    }

    void dfs(int x){
        vis[x] = 1;
        for (int i=1;i<=17;i++){
            if(dep[x]<(1<=0;i--)
            if (fa[x][i]!=fa[y][i]){
            x=fa[x][i];y=fa[y][i];
        }
        if (x==y)return x;
        return fa[x][0];
    }

    int ask(int x,int f){//f:father
        int ans = INF;
        int t = dep[x]-dep[f];
        for (int i=0;i<=17;i++)if(t&(1<

树链剖分

struct TreeChain{
    struct Edge{
        int from, to, nxt;
        Edge(){}
        Edge(int u, int v, int n):
            from(u), to(v), nxt(n){}
    }edges[N];
    int n, E, head[N];

    int tim;
    int siz[N]; //用来保存以x为根的子树节点个数
    int top[N]; //用来保存当前节点的所在链的顶端节点
    int son[N]; //用来保存重儿子
    int dep[N]; //用来保存当前节点的深度
    int fa[N];  //用来保存当前节点的父亲
    int tid[N]; //用来保存树中每个节点剖分后的新编号，线段树
    int Rank[N];//tid反向数组，不一定需要

    inline void AddEdge(int f, int t){
        edges[++E] = Edge(f, t, head[f]);
        head[f] = E;
    }
    inline void Init(int n){
        tim = 0;
        this -> n = n ; E = -1;
        for (int i = 0; i <= n; i++) head[i] = -1;
        for (int i = 0; i <= n; i++) son[i] = -1;
    }

    void dfs1(int u, int father, int d){
        dep[u] = d;
        fa[u] = father;
        siz[u] = 1;
        int nxt;
        for(int i = head[u]; i != -1; i = nxt){
            Edge &e = edges[i]; nxt = e.nxt;
            if (e.to == father) continue;
            dfs1(e.to, u, d + 1);
            siz[u] += siz[e.to];
            if(son[u]==-1 || siz[e.to] > siz[son[u]]) son[u] = e.to;
        }
    }
    void dfs2(int u, int tp){
        top[u] = tp;
        tid[u] = ++tim;
        Rank[tid[u]] = u;
        if (son[u] == -1) return;
        dfs2(son[u], tp);
        int nxt;
        for(int i = head[u]; i != -1; i = nxt){
            Edge &e = edges[i]; nxt = e.nxt;
            if(e.to == son[u] || e.to == fa[u]) continue;
            dfs2(e.to, e.to);
        }
    }
    LL query(int u, int v){
        int f1 = top[u], f2 = top[v];
        LL tmp = 0;
        for (; f1 != f2;){
            if (dep[f1] < dep[f2]){
                swap(f1, f2);
                swap(u, v);
            }
            tmp += T.query(tid[f1], tid[u]);
            u = fa[f1]; f1 = top[u];
        }
        if (dep[u] > dep[v]) swap(u, v);
        return tmp + T.query(tid[u], tid[v]);
    }
} g ;

树分治

poj1741模板题

#include 
#include 
#include 
#include 
using namespace std;
const int N = 1e4 + 7;
const int INF = 0x3f3f3f3f;
int n, k, ans;

struct Edge{
    int from, to, w, nxt;
    Edge(){}
    Edge (int f, int t, int _w, int n):from(f),to(t),w(_w),nxt(n){}
} edges[N * 2];
bool vis[N];
int head[N], E, siz[N], dep[N];

void Init(){
    E = 0;
    memset(head, -1, sizeof(head));
    memset(vis, false, sizeof(vis));
}
void AddEdge(int u,int v,int w){
    edges[E] = Edge(u, v, w, head[u]);
    head[u] = E++;
}

int dfssize(int u, int pre){
    siz[u] = 1;
    for(int i = head[u]; i != -1; i = edges[i].nxt){
        Edge &e = edges[i];
        if(e.to == pre || vis[e.to])continue;
        siz[u] += dfssize(e.to, u);
    }
    return siz[u];
}

//找重心
void dfsroot(int u, int pre, int totnum, int &minn, int &root){
    int maxx = totnum - siz[u];
    for (int i = head[u]; i != -1;i = edges[i].nxt){
        Edge &e = edges[i];
        if(e.to == pre || vis[e.to]) continue;
        dfsroot(e.to, u, totnum, minn, root);
        maxx = max(maxx, siz[e.to]);
    }
    if(maxx < minn){minn = maxx; root = u;}
}

//求每个点离重心的距离
void dfsdep(int u,int pre,int dist, int &num){
    dep[num++] = dist;
    for(int i = head[u]; i != -1; i = edges[i].nxt){
        Edge &e = edges[i];
        if(e.to == pre || vis[e.to])continue;
        dfsdep(e.to, u, dist + e.w, num);
    }
}

//计算以u为根的子树中有多少点对的距离小于等于K
int calc(int u, int d){
    //printf("calc(%d, %d)\n", u, d);
    int ans = 0, num = 0;
    dfsdep(u, -1, d, num);
    sort(dep, dep + num);
    int i = 0, j = num - 1;
    for (; i < j; i++){
        while (dep[i]+dep[j]>k && i

图的割点、桥和双连通分支的基本概念

[点连通度与边连通度]
在一个无向连通图中，如果有一个顶点集合，删除这个顶点集合，以及这个集合中所有顶点相关联的边以
后，原图变成多个连通块，就称这个点集为 割点集合。一个图的 点连通度的定义为，最小割点集合中的顶
点数。
类似的，如果有一个边集合，删除这个边集合以后，原图变成多个连通块，就称这个点集为 割边集合。一
个图的 边连通度的定义为，最小割边集合中的边数。

[双连通图、割点与桥]
如果一个无向连通图的点连通度大于 1，则称该图是 点双连通的(point biconnected)，简称 双连通或 重连通。
一个图有割点，当且仅当这个图的点连通度为 1，则割点集合的唯一元素被称为 割点(cut point)，又叫 关节
点(articulation point)。
如果一个无向连通图的边连通度大于 1，则称该图是 边双连通的(edge biconnected)，简称双连通或重连通。
一个图有桥，当且仅当这个图的边连通度为 1，则割边集合的唯一元素被称为 桥(bridge)，又叫 关节边
(articulation edge) 。
可以看出，点双连通与边双连通都可以简称为双连通，它们之间是有着某种联系的，下文中提到的双连通，
均既可指点双连通，又可指边双连通。

[双连通分支]
在图 G 的所有子图 G’中，如果 G’是双连通的，则称 G’为 双连通子图。如果一个双连通子图 G’它不是任何一
个双连通子图的真子集，则 G’为 极大双连 通子图。 双连通分支(biconnected component)，或 重连通分支，
就是图的极大双连通子图。特殊的，点双连通分支又叫做 块。

[求割点与桥]
该算法是 R.Tarjan 发明的。对图深度优先搜索，定义DFS(u)为u 在搜索树（以下简称为树）中被遍历到的次
序号。定义 Low(u)为u 或u 的子树中能通过非父子边追溯到的最早的节点，即 DFS 序号最小的节点。根据
定义，则有：
Low(u)=Min { DFS(u) DFS(v) (u,v)为后向边(返祖边) 等价于 DFS(v) 为树枝边(父子边) }
一个顶点 u 是割点，当且仅当满足(1)或(2) (1) u 为树根，且u 有多于一个子树。 (2) u 不为树根，且满足存
在(u,v)为树枝边(或称父子边，即 u 为 v 在搜索树中的父亲)，使得 DFS(u)<=Low(v)。
一条无向边(u,v)是桥，当且仅当(u,v)为树枝边，且满足 DFS(u)

[求双连通分支]
下面要分开讨论点双连通分支与边双连通分支的求法。
对于点双连通分支，实际上在求割点的过程中就能顺便把每个点双连通分支求出。建立一个栈，存储当前
双连通分支，在搜索图时，每找到一条树枝边或后向边(非横叉边)，就把这条边加入栈中。如果遇到某时满
足 DFS(u)<=Low(v)，说明 u 是一个割点，同时把边从栈顶一个个取出，直到遇到了边(u,v)，取出的这些边与
其关联的点，组成一个点双连通分支。割点可以属于多个点双连通分支，其余点和每条边只属于且属于一
个点双连通分支。
对于边双连通分支，求法更为简单。只需在求出所有的桥以后，把桥边删除，原图变成了多个连通块，则
每个连通块就是一个边双连通分支。桥不属于任何一个边双连通分支，其余的边和每个顶点都属于且只属
于一个边双连通分支。

[构造双连通图]
一个有桥的连通图，如何把它通过加边变成边双连通图？方法为首先求出所有的桥，然后删除这些桥边，
剩下的每个连通块都是一个双连通子图。把每个双连通子图收缩为一个顶点，再把桥边加回来，最后的这
个图一定是一棵树，边连通度为 1。
统计出树中度为 1 的节点的个数，即为叶节点的个数，记为 leaf。则至少在树上添加(leaf+1)/2 条边，就能
使树达到边二连通，所以至少添加的边数就是(leaf+1)/2。具体方法为，首先把两个最近公共祖先最远的两
个叶节点之间连接一条边，这样可以把这两个点到祖先的路径上所有点收缩到一起，因为一个形成的环一
定是双连通的。然后再找两个最近公共祖先最远的两个叶节点，这样一对一对找完，恰好是(leaf+1)/2 次，
把所有点收缩到了一起。

动态规划

各种背包

背包

const int N = 100007;
struct node {
    int v,w,n;
    node(){}
    node(int x,int y,int z){v=x,w=y,n=z;}
}a[N];

int f[N];
int main(){
    //freopen("fuck.in","r",stdin);
    int cash,n,x,y;
    for (;~scanf("%d%d",&cash,&n);){
        int A = 0;
        for(int i=1;i<=n;i++){
            scanf("%d%d",&x,&y);
            for (int t=0;(1<=a[i].v;j--)
                f[j]=max(f[j],f[j-a[i].v]+a[i].w);

        int ans = 0;//get ans
        for (int i=0;i<=cash;i++) ans=max(ans,f[i]);
        printf("%d\n",ans);
    }
    return 0;
}

多重背包通用模板（单调队列）

int f[N], va[N], vb[N];//MAX_V
void pack(int V,int v,int w,int n){
    if (n==0 || v==0) return;
    if (n==1){  // 01背包
        for (int i=V;i>=v;--i) f[i] = max(f[i], f[i-v] + w);
        return;
    }
    if (n*v >= V-v+1){  // 多重背包(n >= V / v)
        for (int i = v; i <= V; ++i) f[i] = max(f[i], f[i-v] + w);
        return;
    }
    for (int j = 0 ; j < v ; ++j ){
        int *pb = va, *pe = va - 1;
        int *qb = vb, *qe = vb - 1;
        for (int k = j, i = 0;k <= V; k += v, ++i){
            if (pe == pb+n){
                if(*pb == *qb) ++qb;
                ++pb;
            }
            int tt = f[k] - i * w;
            *++pe = tt;
            while (qe >= qb && *qe < tt) --qe;
            *++qe = tt;
            f[k] = *qb + i * w;
        }
    }
}

//主程序调用
        memset(f,0,sizeof(f));    //pack
        for (int i=1;i<=n;i++)
            pack(cash,a[i].v,a[i].w,a[i].n);
        int ans = 0;              //getAns
        for (int i=0;i<=cash;i++) ans=max(ans,f[i]);
        printf("%d\n",ans);

小价值大重量背包问题

	for(int i = 0; i < n; i++) {
	    for(int j = MAXV - 1; j >= v[i] ; j--) {
	        f[j] = min(f[j], f[j - v[i]] + w[i]);
	    }
	}
	int ans = -1;
	for(int i = MAXV - 1; i >= 0; i--) {
	    if (f[i] <= V) {ans = i; break;}
	}
	if (ans != -1) printf("%d\n", ans);
	else printf("No solution\n");

最长上升子序列O(nlogn)

const int MAXN=500010;
int a[MAXN],b[MAXN];
//用二分查找的方法找到一个位置，使得num>b[i-1] 并且num> 1;
        if (num >= b[mid]) low = mid + 1;
        else high = mid-1;
    }
    return low;
}
int DP(int n){
    b[1] = a[1];
    int len = 1;
    for(int i = 2; i <= n; i++){
        if(a[i] >= b[len]){//如果a[i]比b[]数组中最大还大直接插入到后面即可
            b[++len]=a[i];
        }else{//用二分的方法在b[]数组中找出第一个比a[i]大的位置并且让a[i]替代这个位置
            int pos = Search(a[i], 1, len);
            b[pos] = a[i];
        }
    }
    return len;
}

输出LCS序列

string s1,s2;
string lcs2(string s1, string s2){  
    if(s1==""||s2=="") return "";  
    int m=s1.size() + 1;  
    int n=s2.size() + 1;  
    printf("%d %d\n",m,n);  
    int lcs[m][n];  
    memset(lcs, 0, sizeof(lcs));  
    for(int i = 1; i < m; i++)  
        for(int j = 1; j < n; j++){  
            if (s1[i-1]==s2[j-1]) lcs[i][j]=lcs[i-1][j-1]+1;  
            else lcs[i][j]=lcs[i-1][j]>=lcs[i][j-1]?lcs[i-1][j]:lcs[i][j-1];//取上侧或左侧的最大值  
        }  
        int i = m - 2;  
        int j = n - 2;  
        string ss="";  
        while(i!=-1 && j!=-1) {  
            if(s1[i] == s2[j]) {  
                //printf("%c\n",s1[i]);  
                ss += s1[i];  
                i--; j--;  
            } else {  
                if(lcs[i+1][j+1] == lcs[i][j]) {  
                    i--; j--;
                } else {  
                    if (lcs[i][j+1] >= lcs[i+1][j]) i--;  
                    else j--;  
                }  
            }  
        }  
        reverse(ss.begin(), ss.end());//将字符串倒置  
        return ss;  
}  
int main(){  
    while(cin>>s1>>s2){  
        string s=lcs2(s1, s2);  
        cout << s<

数位dp

/*****************
	不要62
******************/
typedef int LL;
LL a[30], dp[30][2], z[30] = {1}, n;
LL dfs(LL pos, LL stat, bool limit) {
    if(pos == -1) return 1;
    if(!limit && dp[pos][stat] != -1) return dp[pos][stat];
    LL up = limit ? a[pos] : 9;
    LL ans = 0;
    for(LL i = 0; i <= up; i++) {
        if(i == 2 && stat) continue;
        if(i == 4) continue;
        ans += dfs(pos - 1, i == 6, limit && i == a[pos]);
    }
    if(!limit) dp[pos][stat] = ans;
    return ans;
}
LL solve(LL x) {
    LL pos = 0;
    while(x) {
        a[pos++] = x % 10;
        x /= 10;
    }
    return dfs(pos - 1, 0, true);
}
int main(){
    memset(dp, -1, sizeof(dp));
    for (LL n1, n2; ~scanf("%d%d", &n1, &n2) && (n1 + n2);) {
        printf("%d\n", solve(n2) - solve(n1 - 1));
    }
    return 0;
}

/*****************
	只要49
******************/
LL a[100], dp[100][2], z[100] = {1}, n;
LL dfs(LL pos, LL stat, bool limit) {
    if(pos == -1) return 0;
    if(!limit && dp[pos][stat] != -1) return dp[pos][stat];
    LL up = limit ? a[pos] : 9, ans = 0;
    for(LL i = 0; i <= up; i++) {
        if(stat && i == 9) ans += limit ? (n % z[pos] + 1) : z[pos];
        else ans += dfs(pos - 1, i == 4, limit && i == a[pos]);
    }
    if(!limit) dp[pos][stat] = ans;
    return ans;
}
LL solve(LL x) {
    LL pos = 0;
    for (; x; x/= 10) a[pos++] = x % 10;
    return dfs(pos - 1, 0, true);
}
int main(){
    for(int i = 1;i < 30; i++) z[i] = z[i - 1] * 10;
    memset(dp, -1, sizeof(dp));
    int t; cin >> t;
    while(t--) {
        cin >> n;
        cout << solve(n) << endl;
    }
    return 0;
}

第二种方法

LL n, dp[25][3];  
//dp[i][j]:长度为i，状态为j  
int digit[25];
//nstatus: 0：不含49, 1：不含49但末尾是4, 2 :含49  
LL DFS(int pos, int status, int limit){  
    if(pos <= 0) // 如果到了已经枚举了最后一位，并且在枚举的过程中有49序列出现  
        return status==2;//注意是 ==  
    if(!limit && dp[pos][status]!=-1)   //对于有限制的询问我们是不能够记忆化的  
        return dp[pos][status];  
    LL ans = 0;  
    int End = limit?digit[pos]:9;   // 确定这一位的上限是多少  
    for(int i = 0; i <= End; i++){   // 每一位有这么多的选择  
        int nstatus = status;       // 有点else s = statu 的意思
        if(status==0 && i==4)//高位不含49，并且末尾不是4 ，现在末尾添4返回1状态  
            nstatus = 1;
        else if(status==1 && i!=4 && i!=9)//高位不含49，且末尾是4，现在末尾添加的不是4返回0状态  
            nstatus = 0;
        else if(status==1 && i==9)//高位不含49，且末尾是4，现在末尾添加9返回2状态  
            nstatus = 2;
        ans+=DFS(pos-1, nstatus, limit && i==End);  
    }  
    if(!limit)  
        dp[pos][status]=ans;  
    return ans;  
}  

第三种方法·没有DFS的纯DP

LL dp[27][3];  
int c[27];  
//dp[i][j]:长度为i的数的第j种状态  
//dp[i][0]:长度为i但是不包含49的方案数  
//dp[i][1]:长度为i且不含49但是以9开头的数字的方案数  
//dp[i][2]:长度为i且包含49的方案数  
void init()  {  
    memset(dp,0,sizeof(dp));  
    dp[0][0] = 1;  
    for(int i = 1; i <= 20; i++){  
        dp[i][0] = dp[i-1][0]*10-dp[i-1][1];  
        dp[i][1] = dp[i-1][0]*1;  
        dp[i][2] = dp[i-1][2]*10+dp[i-1][1];  
    }  
}  

/*****************
被13整除且包含“13”
******************/
typedef int LL;
LL a[30], dp[30][15][3], z[30] = {1}, n;
LL dfs(LL pos, LL mod, LL stat, bool limit) {
    if(pos == -1) return mod == 0 && stat == 2;
    if(!limit && dp[pos][mod][stat] != -1) return dp[pos][mod][stat];
    LL up = limit ? a[pos] : 9;
    LL ans = 0;
    for(LL i = 0; i <= up; i++) {
        LL ns = stat;
        if(stat == 0 && i == 1) ns = 1;
        if(stat == 1 && i != 1) ns = 0;
        if(stat == 1 && i == 3) ns = 2;
        ans += dfs(pos - 1, (mod * 10 + i) % 13, ns, limit && i == a[pos]);
    }
    if(!limit) dp[pos][mod][stat] = ans;
    return ans;
}
LL solve(LL x) {
    LL pos = 0;
    for (; x; x/=10) a[pos++] = x % 10;
    return dfs(pos - 1, 0, 0, true);
}
int main(){
    memset(dp, -1, sizeof(dp));
    for(LL i = 1; i < 30; i++) z[i] = z[i - 1] * 10;
    while(cin >> n) cout << solve(n)<< endl;
    return 0;
}

区间调度问题

问题分类	策略	数据结构	哪端排序	复杂度
最多区间调度	贪心	一维数组	结束时间	O(nlogn)
最大区间调度	动态规划	一维数组	结束时间	O(nlogn)
带权区间调度	动态规划	一维数组	结束时间	O(nlogn)
最小区间覆盖	贪心	一维数组	开始时间	O(nlogn)
最大区间重叠	贪心	multiset	结束时间	O(nlogn)
最大区间重叠	贪心	优先队列	开始时间	O(nlogn)
最大区间重叠	拆点	一维数组	-	O(n)
机器调度	回溯	二维数组	-	O(k^n)
机器调度	贪心	优先队列	-	O(nlogn)

判断区间重叠的条件：e1 >= s2 && s1 <= e2

在涉及区间重叠的问题上，一般都会先进行排序。

最优化问题都可以通过某种搜索获得最优解，最多区间调度问题，其解空间为一棵二叉子集树，某个区间选或者不选构成了两个分支。

最大区间重叠又称最少工人调度，在有人数限制的情况下运用结束时间排序更好，相当于最多区间调度问题了。
维护每个工人的结束时间，优先选择结束时间晚的工人。

机器调度运用K叉树得到最优解，最长处理时间优先贪心只能近似解。

已经证明，当机器数(或称工序数)m≥3时，流水作业调度问题是一个NP-hard问题。
已经证明，机器调度问题是NP-hard问题（多机器并行）

人数限制为K的最多区间调度问题：

#include 
#include
#include
#include 
#include 
#include 
using namespace std;
typedef long long LL;
const int maxn = 1e5 + 10;
typedef pairP;
P p[maxn];
LL a[maxn];
bool cmp(const P& x,const P& y){
    if(x.second != y.second) return x.second < y.second;
    return x.first < y.first;
}
int main(){
    LL n,k;
    multiset sets;
    while(scanf("%lld%lld",&n,&k) == 2){
        sets.clear();
        for(int i = 0;i < n;i++){
            scanf("%lld%lld",&p[i].first,&p[i].second);
        }
        sort(p,p + n,cmp);
        multiset::iterator ite;
        int cnt = 0;
        while(k--) sets.insert(0);
        for(int i = 0; i < n; i++) {
            P point = p[i];
            if(*sets.begin() > point.first) continue;
            if(*sets.begin() == point.first) {
                cnt++;
                sets.erase(sets.begin());
                sets.insert(point.second);
            } else {
                ite = sets.upper_bound(point.first);
                ite--;
                cnt++;
                sets.erase(ite);
                sets.insert(point.second);
            }
        }
        cout << cnt << endl;
    }
}

斜率优化

#include
using namespace std;
const double eps = 1e-8;
typedef long long LL;
const int MAXN=500010;
int dp[MAXN], sum[MAXN], head,tail,n,m;
int q[MAXN];  // 单调队列

// dp[i]= min{ dp[j]+M+(sum[i]-sum[j])^2 }; 
// dp[i] 化简为 dp[i] = f[i] + b[i] * min(y[j] + x[j] * a[i]) 其中x[j]为单调减 
// 此题a[i]单调减，故可以用单调队列，否则用二分查找 
int getDP(int i,int j){
    return dp[j]+m+(sum[i]-sum[j])*(sum[i]-sum[j]);
}
int getUP(int j,int k){ //yj-yk部分
    return dp[j]+sum[j]*sum[j]-(dp[k]+sum[k]*sum[k]);
}
int getDOWN(int j,int k){ //xj-xk的部分
    return 2*(sum[j]-sum[k]);
}
int main(){
    while(scanf("%d%d",&n,&m)==2){
        for(int i=1;i<=n;i++)
           scanf("%d",&sum[i]);
        sum[0]=dp[0]=0;
        for(int i=1;i<=n;i++)
           sum[i]+=sum[i-1];
        head=tail=0;
        q[tail++]=0;
        for(int i=1;i<=n;i++){
            //把斜率转成相乘，注意顺序，否则不等号方向会改变的
            while(head+1

计算几何

大部分计算几何模板小红书可以翻到，还可以用

point && line

const int MAXN = 1e6 + 5;
const double eps = 1e-8;

int cmp(double x) {
    if(fabs(x) < eps) return 0;
    if(x > 0) return 1;
    return -1;
}

const double pi = acos(-1.0);
inline double sqr(double x) {
    return x * x;
}
struct point{
    double x, y;
    point(){}
    point(double a, double b) : x(a), y(b) {}
    void input() {
        scanf("%lf%lf", &x, &y);
    }
    friend point operator + (const point &a, const point &b) {
        return point(a.x + b.x, a.y + b.y);
    }
    friend point operator - (const point &a, const point &b) {
        return point(a.x - b.x, a.y - b.y);
    }
    friend bool operator == (const point &a, const point &b) {
        return cmp(a.x - b.x) == 0 && cmp(a.y - b.y) == 0;
    }
    friend point operator * (const point &a, const double &b) {
        return point(a.x * b, a.y * b);
    }
    friend point operator * (const double &a, const point &b) {
        return point(a * b.x, a * b.y);
    }
    friend point operator / (const point &a, const double &b) {
        return point(a.x / b, a.y / b);
    }
    double norm() {
        return sqrt(sqr(x) + sqr(y));
    }
};
double det(const point &a, const point &b) {
    return a.x * b.y - a.y * b.x;
}
double dot(const point &a, const point &b) {
    return a.x * b.x + a.y * b.y;
}
double dist(const point &a, const point &b) {
    return (a - b).norm();
}
point rotate_point(const point &p, double A) {
    double tx = p.x, ty = p.y;
    return point(tx * cos(A) - ty * sin(A), tx * sin(A) + ty * cos(A));
}
struct line{
    point a, b;
    line(){}
    line(point x, point y) : a(x), b(y){}
};
line point_make_line(const point a, const point b) {
    return line(a, b);
}
double dis_point_segment(const point p, const point s, const point t) {
    if(cmp(dot(p-s, t-s)) < 0) return (p - s).norm();
    if(cmp(dot(p-t, s-t)) < 0) return (p - t).norm();
    return fabs(det(s-p, t-p)/dist(s,t));
}
void PointProjLine(const point p,const point s, const point t,point &cp){
    double r = dot((t-s), (p-s))/dot(t-s, t-s);
    cp=s+r*(t-s);
}
bool PointOnSegment(point p, point s, point t){
    return cmp(det(p-s, t-s))==0 && cmp(dot(p-s,p-t))<=0;
}
bool parallel(line a,line b){
    return !cmp(det(a.a-a.b,b.a-b.b));
}
bool line_make_point(line a,line b,point &res){
    if (parallel(a,b)) return false;
    double s1=det(a.a-b.a,b.b-b.a);
    double s2=det(a.b-b.a,b.b-b.a);
    res=(s1*a.b-s2*a.a)/(s1-s2);
    return true;
}
line move_d(line a, const double &len) {
    point d = a.b - a.a;
    d = d / d.norm();
    d = rotate_point(d, pi/2);
    return line(a.a + d*len, a.b + d * len);
}

极角排序

预处理

const double eps = 1e-6;  
bool dy(double x,double y)  {   return x > y + eps;} // x > y   
bool xy(double x,double y)  {   return x < y - eps;} // x < y   
bool dyd(double x,double y) {   return x > y - eps;} // x >= y   
bool xyd(double x,double y) {   return x < y + eps;}     // x <= y   
bool dd(double x,double y)  {   return fabs( x - y ) < eps;}  // x == y  

atan2排序

bool cmp(point& a,point& b){    
    double t1 = atan2(a.y - C.y, a.x - C.x);  
    double t2 = atan2(b.y - C.y, b.x - C.x);  
    if( dd(t1, t2) ) return xy(fabs(a.x),fabs(b.x));  
    return xy(a.t, b.t);    
}  

象限极角排序代码

int quad(point a){// 判断象限的函数，每个象限包括半个坐标轴   
    if( dy(a.x,0) && xyd(a.y,0) ) return 1;  
    if( xyd(a.x,0) && dy(a.y,0) ) return 2;  
    if( xy(a.x,0) && xyd(a.y,0) ) return 3;  
    if( dyd(a.x,0) && xy(a.y,0) ) return 4;  
}   
bool cmp(point& a,point& b){    
    point p1 = a,p2 = b;  
    p1.x -= C.x; p1.y -= C.y;  
    p2.x -= C.x; p2.y -= C.y;  
    int l1,l2;  
    l1 = quad(p1); l2 = quad(p2);  
    if( l1 == l2 ){  
        double c = crossProduct(C,a,b);  
        return xy(c,0) || dd(c,0.0) && xy(fabs(a.x),fabs(b.x));  
    }  
    return l1 < l2;  
}   

线段相交（向量）

用的时候改int

struct point{
    double x, y;

    point():x(0), y(0){}
    point(double _x, double _y): x(_x),y(_y){}
    inline void read(){
    	scanf("%lf%lf", &x, &y);
    }
    point operator + (const point &a) const {
        return point(x+a.x, y+a.y);
    }
    point operator - (const point &a) const {
        return point(x-a.x, y-a.y);
    }
    point operator * (const double &k) const {
    	return point(x * k, y * k);
    }
    double operator ^ (const point &a) const {  // det
        return x*a.y - y*a.x;
    }
    double dis(const point &b) {
    	return (x-b.x)*(x-b.x) + (y-b.y)*(y-b.y);
    }
    inline void print(){
    	printf("point: (%.2lf, %.2lf)\n", x, y);
    }
    bool onSeg(point P1, point P2){
    	point Q = point(x, y);
    	if (min(P1.x,P2.x) > Q.x || Q.x > max(P1.x,P2.x)) return false;
        if (min(P1.y,P2.y) > Q.y || Q.y > max(P1.y,P2.y)) return false;
        double ans = fabs((Q - P1) ^ (Q - P2));
        //printf("??? = %.4lf\n", ans);
		if (fabs((Q - P1) ^ (Q - P2)) > 0) return false;
    	return true;
    }
} A, B, C;

double s(point p, point a, point b){
	return fabs((p - a) ^ (p - b));
}
bool inTra(point P, point A, point B, point C){
	double s1 = s(P, A, B), s2 = s(P, B, C), s3 = s(P, C, A);
	if (s1 == 0 || s2 == 0 || s3 == 0) return false;
	double a =  s1 + s2 + s3;
	double b = s(A, B, C);
	//printf("%.2lf\n", a-b);
	return fabs(a - b) == 0.;
}

bool segXseg(point p1, point p2, point p3, point p4){
	// attention, not good
	if (p1.onSeg(p3, p4) || p2.onSeg(p3, p4)) return false;
	if (p3.onSeg(p1, p2) || p4.onSeg(p1, p2)) return false;
	//---------------------------------------------
    if (max(p1.x, p2.x) < min(p3.x, p4.x)) return 0;
    if (max(p1.y, p2.y) < min(p3.y, p4.y)) return 0;
    if (max(p3.x, p4.x) < min(p1.x, p2.x)) return 0;
    if (max(p3.y, p4.y) < min(p1.y, p2.y)) return 0;//ju xin shi yan

    double x = (p3 - p1) ^ (p2 - p1);
    double y = (p4 - p1) ^ (p2 - p1);
    double z = (p1 - p3) ^ (p4 - p3);
    double w = (p2 - p3) ^ (p4 - p3); //KuaLi
    return x*y <= 0 && z*w <= 0;
}

bool xj(point p1, point p2, point A, point B, point C){  //xiangjiao
	//for (double k = 0.01; k < 1; k += 0.01) // seg & tra
		//if (inTra((p1*k + p2*(1-k)), A, B, C)) return true;
	if (inTra(p1*0.01 + p2*0.99, A, B, C)) return true;
	if (inTra(p1*0.99 + p2*0.01, A, B, C)) return true;
	if (segXseg(p1, p2, A, B)) return true;
	if (segXseg(p1, p2, A, C)) return true;
	if (segXseg(p1, p2, C, B)) return true;
	return false;
}

经纬度公式

const long double pi = acos(-1.0);
const long double R = 6371.0;
long double haversin(long double a){
	return sin(a / 2) * sin(a / 2);
}
long double dist(P a, P b){
	long double p = haversin((b.x - a.x) * pi / 180) + cos(a.x * pi / 180) * 
		cos(b.x * pi / 180) * haversin((b.y - a.y) * pi / 180);
	return asin(sqrt(p)) * 2 * R;
}

其他

莫队入门

题意已知一个长度为n的数列 (0 ≤ ai ≤ 1 000 000) ，给m个区间，问每个区间有多少个子区间xor和为k
(1 ≤ n, m ≤ 100 000, 0 ≤ k ≤ 1 000 000)
莫队算法
如果你知道了[L,R]的答案。你可以在O(1)的时间下得到[L,R-1]和[L,R+1]和[L-1,R]和[L+1,R]的答案的话。就可以使用莫队算法。
先对序列分块。然后对于所有询问按照L所在块的大小排序。如果一样再按照R排序。然后按照排序后的顺序计算。复杂度O(n^1.5)
对于本题
我们设定 sum[i] 为[1, i]区间内的异或和，对于区间[a, b]的异或和为sum[b] ^ sum[a-1]。如果区间 [a, b] 的异或和为k，则有sum[b] ^ sum[a-1] == k，由于异或的性质可以推论 出：sum[b] ^ k == sum[a-1]，sum[a-1] ^ k == sum[b]。

const int maxn = 2e6+7;  
struct node {int l,r,id;}q[maxn];  
int a[maxn],pos[maxn];  
LL ans[maxn],sum[maxn];  
int n,m,k;  
LL Ans=0;  
bool cmp(node a,node b){  
    if(pos[a.l]!=pos[b.l]) return pos[a.l]l){dele(l-1);l++;}  
            while(q[i].rr){r++;add(r);}  
            ans[q[i].id]=Ans;  
        }  
        for(i=1;i<=m;i++) printf("%I64d\n",ans[i]);  
    }  
    return 0;  
}  

模拟退火

double anss = 0;  
for(int i=0;i 1e-6; i++) {  
        flag = -1;  
        for (int k = 0; k < 40; k++) {  
            double ang = (rand()%1000+1)/1000.0*10*pi;    
            tmp.x = ans.x + step * cos(ang);  
            tmp.y = ans.y + step * sin(ang);  
            C.p = tmp;  
            if (ncost < cal_cross(C,p,n)) {  
                ncost = cal_cross(C,p,n);  
                flag = 1;  
                ans = tmp;  
            }  
        }  
        if (flag == -1) step *= 0.8;  
    }  
    if(ncost>acost){  
        acost = ncost;  
        cnt = ans;  
    }  
}  

C++高精度

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
int B = 10;

const int MAXN = 6000;
char s1[MAXN], s2[MAXN];

struct bign{ // big number
    int len, s[MAXN];
    
    bign (){
        memset(s, 0, sizeof(s));
        len = 1;
    }
    bign (int num) { *this = num; }
    bign (const char *num) { *this = num; }
    bign operator = (const int num){
        char s[MAXN];
        sprintf(s, "%d", num);
        *this = s;
        return *this;
    }
	void clean(){
        while(len > 1 && !s[len-1]) len--;
    } 
    bign operator = (const char *num){
    	memset(s, 0, sizeof s);
    	len = strlen(num);
        for(int i = 0; i < len; i++) {
        	if (isdigit(num[len-i-1])) s[i] = num[len-i-1] - '0';
        	else s[i] = num[len-i-1] - 'A' + 10;
        }
        clean();
        return *this;
    }

    bign operator + (const bign &b) const{
        bign c;
		c.len = max(len, b.len);
        for (int i = 0; i < c.len; i++){
			c.s[i] += s[i] + b.s[i];
            c.s[i+1] += c.s[i] / B; // B default = 10
            c.s[i] %= B;
        }
        if (c.s[c.len]) c.len++;
        c.clean();
        return c;
    }
    
    bign operator += (const bign &b){
        *this = *this + b;
        return *this;
    }

    bign operator * (const bign &b) {//*
        bign c;
        c.len = len + b.len;
        for(int i = 0; i < len; i++)
            for(int j = 0; j < b.len; j++)
                c.s[i+j] += s[i] * b.s[j];
        for(int i = 0; i < c.len; i++, c.s[i] %= 10)
            c.s[i+1] += c.s[i]/10;
        c.clean();
        return c;
    }
    bign operator *= (const bign &b){
        *this = *this * b;
        return *this;
    }
    bign operator - (const bign &b){
        bign c;
        c.len = 0;
        for(int i = 0, g = 0; i < len; i++){
            int x = s[i] - g;
            if(i < b.len) x -= b.s[i];
            if(x >= 0) g = 0;
            else{
                g = 1;
                x += 10;
            }
            c.s[c.len++] = x;
        }
        c.clean();
        return c;
    }
    bign operator -= (const bign &b){
        *this = *this - b;
        return *this;
    }
    bign operator / (const bign &b){
        bign c, f = 0;
        for(int i = len-1; i >= 0; i--){
            f = f*10;
            f.s[0] = s[i];
            while(f > b || f == b){
                f -= b;
                c.s[i]++;
            }
        }
        c.len = len;
        c.clean();
        return c;
    }
    bign operator /= (const bign &b){
        *this  = *this / b;
        return *this;
    }
    bign operator % (const bign &b){
        bign r = *this / b;
        r = *this - r*b;
        return r;
    }
    bign operator %= (const bign &b){
        *this = *this % b;
        return *this;
    }
    bool operator < (const bign &b){
        if(len != b.len) return len < b.len;
        for(int i = len-1; i >= 0; i--){
            if(s[i] != b.s[i]) return s[i] < b.s[i];
        }
        return false;
    }
    bool operator > (const bign &b){
        if(len != b.len) return len > b.len;
        for(int i = len-1; i >= 0; i--){
            if(s[i] != b.s[i]) return s[i] > b.s[i];
        }
        return false;
    }
    bool operator == (const bign &b){
        return !(*this > b) && !(*this < b);
    }
    string str() const{
        string res = "";
        for (int i = 0; i < len; i++) {
        	if (s[i] < 10) res = char(s[i]+'0') + res;
        	else res = char(s[i] + 'A' - 10) + res;
        }
        return res;
    }
} a, b, c;


int main(){
    while(~scanf("%d", &B)){
    	scanf("%s%s", s1, s2);
        a = bign(s1);
        b = bign(s2);
        c = a + b;
        cout << c.str() << endl;
    }
    return 0;
}

Java大整数

—：在java中的基本头文件（java中叫包）

import java.io.*
importjava.util.*       我们所用的输入scanner在这个包中
importjava.math.*          我们下面要用到的BigInteger就这这个包中

二：输入与输出

读入 Scanner cin=new Scanner（System.in）
While(cin.hasNext())   //相当于C语言中的！=EOF
n = cin.nextInt();       //输入一个int型整数
n = cin.nextBigInteger();   //输入一个大整数
System.out.print(n);      //输出n但不换行
System.out.println();     //换行
System.out.println(n);    //输出n并换行
System.out.printf(“%d\n”,n);     //类似C语言中的输出

三：定义变量

定义单个变量：
int a,b,c;      //和C++ 中无区别
BigInteger  a;   //定义大数变量a
BigIntegerb= new BigInteger("2");   //定义大数变量 b赋值为 2；
BigDecimaln；     //定义大浮点数类 n；

定于数组：
int a[]= new int[10]   //定义长度为10的数组a
BigInteger  b[] =new BigInteger[100]   //定义长度为100的数组a

四：表示范围

布尔型 boolean 1 true,false false
字节型 byte 8 -128-127 0
字符型 char 16 ‘\u000’-\uffff ‘\u0000’
短整型 short 16 -32768-32767 0
整型 int 32 -2147483648,2147483647 0
长整型 long 64 -9.22E18,9.22E18 0
浮点型 float 32 1.4E-45-3.4028E+38 0.0
双精度型 double 64 4.9E-324,1.7977E+308 0.0
BigInteger任意大的数，原则上只要你的计算机内存足够大，可以有无限位

五：常用的一些操作

A=BigInteger.ONE;   //把0赋给A
B=BigInteger. valueOf (3);    //把3赋给B；
A[i]=BigInteger. valueOf (10);    //把10赋给A[i]
c=a.add(b)        //把a与b相加并赋给c
c=a.subtract(b)   //把a与b相减并赋给c
c=a.multiply(b)   //把a与b相乘并赋给c
c=a.divide(b)     //把a与b相除并赋给c
c=a.mod(b)        // 相当于a%b
a.pow(b)          //相当于a^b
a.compareTo(b)：      //根据该数值是小于、等于、或大于a 返回 -1、0 或 1；
a.equals(b)：    //判断两数是否相等，也可以用compareTo来代替；
a.min(b)，a.max(b)：  //取两个数的较小、大者；

例题：hdu5920
题意：求一个数用50个以内的回文数加起来的方案

import java.math.*;
//import java.io.*;
import java.util.*;
public class Main {
    public static BigInteger fanzhuan(BigInteger n){
        //System.out.println("fanzhuan" + n);
        int k = String.valueOf(n).length();
        BigInteger ret = BigInteger.ZERO;
        for (int i=1;i<=k;i++){
            ret = ret.add(n.mod(BigInteger.TEN));
            ret = ret.multiply(BigInteger.TEN);
            n = n.divide(BigInteger.TEN);
        }
        ret = ret.divide(BigInteger.TEN);
        return ret;
    }
    public static void main(String[] argv){
        Scanner cin = new Scanner(System.in);
        int T =cin.nextInt();
        for (int cas=1;cas<=T;cas++){
            BigInteger n = cin.nextBigInteger();
            int N = String.valueOf(n).length();
            int A = 0;
            BigInteger ans[] = new BigInteger[55];
            for (;N>1;){
                //System.out.println("n=" + n);
                BigInteger one0 = BigInteger.TEN.pow(N>>1);
                BigInteger half = n.divide(one0);
                if (N<=2){
                    if (N==1){ 
                        ans[++A] = n; 
                        n = BigInteger.ZERO;
                        break;
                    }else {//2 wei
                        if (n.compareTo(BigInteger.valueOf(19))==0){
                            ans[++A] = BigInteger.valueOf(11); 
                            ans[++A] = BigInteger.valueOf( 8); 
                            n = BigInteger.ZERO;
                            break;
                        }else if (n.compareTo(BigInteger.valueOf(19))==-1){
                            ans[++A] = BigInteger.valueOf(9);
                            ans[++A] = n.subtract(BigInteger.valueOf(9));
                            n = BigInteger.ZERO;
                            break;
                        }//else continue;
                    }
                }
                half = half.subtract(BigInteger.ONE);
                //System.out.println("half=" + half);
                BigInteger fan = fanzhuan(half);
                if (N%2>0) fan = fan.mod(one0);
                //System.out.println("fan=" + fan);
                BigInteger jan = half.multiply(one0).add(fan);
                //System.out.println("jan=" + jan);
                ans[++A] = jan ;
                n = n.subtract(jan);
                N = String.valueOf(n).length();
            }
            if (n.compareTo(BigInteger.ZERO)==1)ans[++A] = n;
            System.out.printf("Case #%d:\n%d\n",cas,A);
            for (int i=1;i<=A;i++){
                System.out.println(ans[i]);
            }
        }
        cin.close();
    }
}

python IO

每次input一行

while True:
	try:
		a = input()
	except EOFError:
		break

# if u want a + b
print(sum(map(int, input().split())))

头文件

#include 
#pragma comment(linker, "/STACK:1024000000,1024000000") 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

输入挂

const int BUFSIZE = 100 * 1024 * 1024;
char Buf[BUFSIZE + 1], *buf = Buf;
template
void read(T &a){
    for(a=0; *buf<'0' || *buf>'9'; buf++);
    while(*buf>='0' && *buf<='9'){
        a = a*10+(*buf-'0'); buf++;
    }
}

对拍模板,freopen

FOR ACM OI
在linux的shell脚本对拍命令
执行方法：在终端下，进入当前目录，输入"sh ./nick.sh",（其中nick.sh为当前shell脚本名）
ubuntu14.04下实测成功

while true; do
./make>tmp.in #出数据
./tmp<tmp.in>tmp.out #被测程序
./tmp2<tmp.in>tmp2.out #正确（暴力）程序
if diff tmp.out tmp2.out; then #比较两个输出文件
printf AC #结果相同显示AC
else
echo WA #结果不同显示WA，并退出
#cat tmp.out tmp2.out
exit 0
fi #if的结束标志,与C语言相反，0为真
done # while的结束标志

#BY NICK WONG 2014-08-29
#在终端下，进入当前目录，输入"sh ./nick.sh",（其中nick.sh为当前shell脚本名） '#'表示单行注释
#diff在两文件相同时返回空串

freopen的关闭

    freopen("in.txt", "r", stdin);
    fclose(stdin);
    freopen("CON", "r", stdin);
    int m;
    cin >> m;
    cout << m;

/*
windows 下对拍

:again
D:\cb-work4\gen\bin\Debug\gen.exe
D:\cb-work4\duiA\bin\Debug\duiA.exe
D:\cb-work4\duiB\bin\Debug\duiB.exe
fc C:\Users\admin\Desktop\duipai\out1.txt C:\Users\admin\Desktop\duipai\out2.txt
if not errorlevel 1 goto again
pause

linux 下对拍

if diff test.out test.ans;then
echo AC
else
echo WA
exit 0
fi
done
*/