matlab calibration toolbox-Matlab标定工具箱使用（单目标定和双目标定）

转载自：https://blog.csdn.net/kaspar1992/article/details/54344965

英文网址：

http://www.vision.caltech.edu/bouguetj/calib_doc/index.html#examples

http://www.vision.caltech.edu/bouguetj/calib_doc/htmls/example.html

http://www.vision.caltech.edu/bouguetj/calib_doc/htmls/example5.html

转载请注明：http://blog.csdn.net/kaspar1992

CSDN——matlab工具箱下载地址：http://download.csdn.net/detail/kaspar1992/9783397

matlab calibration toolbox-Matlab标定工具箱使用

1. 单目标定

1. 这个教程将带你完整地利用20到25张平面棋盘格图像进行相机标定。

2. 这个教程将让你学会如何使用所有工具箱的特征：载入图像、提取图像角点、运行标定引擎、显示结果、控制精度

3. 添加和删减图像、图像矫正、导出标定不同格式的数据...这个教程对于刚开始使用工具箱的人来说非常重要。

4.  

5. 首先下载Matlab标定工具箱：

6. [http://www.vision.caltech.edu/bouguetj/calib_doc/download/index.html]

7.  

8. 将其解压到Matlab的工作目录下，然后将其包含到matlab的工作路径下。

9. 运行

calib_gui就可以打开matlab标定工具箱主界面：

下载标定案例图片

1. 1、将标定用的图像单独存放于calib_example文件夹中。

2. 2、在matlab中，进入到calib_example文件夹中。

3.  

4. 3、读取图像：

5.  

6. 点击标定工具窗口中的“Image names”按钮。输入标定图像的基名和图像的格式（例如标定图像的名称分别是

7. Img1.jpg,Img2.jpg,Img3.jpg...基名就是

Img

1. 图像格式就是jpg）

2. 然后所有的标定图像都将加载进来，其对应的变量名分别是I_1,I_2，...图像数量对应的变量是n_ima。

3. 载入完图像之后的图像如下：

之后载入的图像将以缩略图的形式显示出来：

一些图像内存不足的问题在此就不作详细的介绍了，现在一般的电脑RAM都是足够来做标定的。

1. 4、提取角点：

2. 点击标定工具箱上的“Extract grid corners”按钮。在matlab命令行会出现如下提示信息：

1. 直接按“Enter”（没有参数）选择所有的图像，否则就需要输入图像索引如[2 5 8 10 12]来提取这些图像中的

2. 角点。然后通过直接输入“Enter”来选择默认的角点寻找窗口尺寸：wintx=winty=5。这就产生了一个11X11个像素

3. 有效的窗口尺寸：

1. 角点提取引擎有一个对网格中的方格个数进行计数的自动机制。这个工具尤其对于图像数量大的时候非常便利，因为

2. 用户不需要手工地输入X和Y方向方格的数量。然而对于极少数场合，这个工具可能不能得到正确的方格数量，这种情况

3. 只有当镜头有很大的畸变。在这种情况下，角点提取这个过程，工具箱提供了一个可选项可供用户关闭自动计数方格。

4. 在这个特殊的模式下，使用者优先对每张图像使用方格自动计数功能，因此，直接按“Enter”键默认。（通常情况

5. 下都使用默认形式，然后如果确实有需要，再重新处理几张有问题的图像。）

然后第一张标定图像就会显示出来：

1. 然后点击长方形棋盘格的四个边角点。选择的位置在下图中显示出来（注意：尽量精确地点击这四个角点，控制

2. 在实际角点的5个像素范围内，否则一些角点可能会被检测器丢失掉）

3.  

4. 点击的顺序规则：第一个点被用来作为棋盘格坐标系的原点。其他三个点可以以任何顺序点击。第一个点击的的点

5. 非常重要，尤其是对于多相机的情况（例如当计算几个相机在空间之间的相互关系的时候）。当处理多相机系统时

6. 对于不同的相机标定图像需要总是选择同一个棋盘格坐标系。三维标定可以运行

stereo_gui.m（后文有介绍，双目标定部分）

第一个点的选择非常重要，一定要注意

经过上面的步骤之后，标定棋盘的边界就显示出来了：

输入网格中每个方格在X和Y方向上的尺寸dX和dY（在这里，dX=dY=30mm=default values）（需要根据自己的棋盘做调整）：

1. 注意：你可以直接输入“Enter”直接用默认参数，程序会自动对各个方向的方格数进行计数，然后在显示出没有

2. 畸变的预估角点。

1. 如果预估的角点很接近实际的图像角点，则下面的步骤就可以略过了（如果没有那么大的图像畸变）。在现在的

2. 图像中：预估的角点足够接近实际的图像角点。因此，没有必要通过输入一个猜测的径向畸变系数去帮助软件去

3. 检测图像角点。直接输入“Enter”，会使用这些初始的预估角点作为提取的角点：

然后图像角点就被自动地提取出来了，然后显示出来，如下图所示：

1. 角点以大约0.1个像素的精度被提取出来。

2. 对第2、3、4...图像采用上述同样的步骤。如下图是将图像2、3、4..图像的角点提取出来：

1. 从上面观察到方格尺寸dX、dY总是被保持在它们的初始值（30mm）.

2.  

3. 有时，预估的角点不是那么足够地接近实际图像角点，在这种情况下，就有必要通过输入一个镜头畸变系数来调整

4. 预估角点。第15张图像就是这种情况，在这张图像中，预估角点的图像如下图所示：

1. 可以看到一些预估角点和实际图像的角点的差距很大，这样就会导致错误的角点提取。而这产生的原因就是因为

2. 图像畸变。为了帮助系统更好地判断角点的位置，用户可以手动地输入一个镜头

畸变系数Kc

1. .为了输入镜头畸变

2. 系数，我们需要在那个问题“Need of an initial guess for distortion?”这里输入一个非空参数，这里

3. 我们输入畸变系数Kc=-0.3（一般这个系数在-1到1之间）。如下图所示：

根据这个畸变系数，新的预估角点位置如下图所示：

1. 如果新的预估角点足够接近实际的图像角点（如上图所示），则输入任何不为空的字符（如1）作为问题“Satisfied

2. with distortion?”的回答。然后亚像素角点的位置就会使用新的带有图像畸变的预估位置进行计算。

1. 如果我们还不满意，我们可以输入一个空的字符串作为问题"Satisfied with distortion?"（直接输入“Enter”）

2. 然后尝试一个新的畸变系数Kc。你可能会重复很多次这样的过程直到对结果满意为止。

注意：上面用到的畸变的值仅仅是用来帮助提取角点，其不会影响下面主要的标定过程。换句话说，这里的畸变系数并不会作为最终的畸变结果，也不会用于优化畸变系数的初始值

最后检测到的角点如下图所示：

1. 对剩下的几张图片重复上述过程（图片16-20）.然而对这些图像，不要使用预先的畸变系数这个选项，尽管提取的

2. 角点不是很正确。在下面的步骤中，我们将纠正它们（在这个例子中，我们不会使用畸变系数这个选项用于图像15

3. 但是这样对于我们证明很有用）。

1. 在角点提取之后，就会自动产生一个calib_data.mat的matlab数据文件。这个文件包含了整个角点提取过程中

2. 的所有信息（图像坐标，对应的3D网格坐标，网格尺寸....）。这个文件是为了防止matlab突然崩溃而创立的。

3. 载入这个文件可以避免你又重复一遍上面的过程。

4.  

5. 在你自己标定的过程中，当图像中有大的畸变的时候，这个程序可能不能够在网格中自动对方格进行计数，在这种

6. 情况下，X和Y方向的方格数量必须手动输入。这在这个例子中没有出现这种情况。

7.  

8. 在你自己做标定的时候，还有一种情况会出现。如果镜头畸变非常严重（像鱼眼镜头），这个基于单个畸变系数的

9. 简化的指导工具对角点的初始预估可能就不够用。

10. 对于这几种麻烦的情况，在工具箱中的一个脚本程序支持完全手动的角点提取（例如每次点击一个角点）。脚本文

11. 件叫做“manual_corner_exteaction.m”（在内存优化模式下，你可以使用"manual_corner_

12. extraction_no_read.m"），并且应该在传统的角点提取代码运行之后才能执行这个代码。（因为它基于传统的

13. 角点提取的一些数据）。

14.  

15. 显然，这种角点提取的方法当图像数量多的时候是非常耗时的。因为它作为当前面的尝试都失败的情况下的一种

16. 救命稻草。但完全可以不用太担心这个，在这个例子中不会出现这种情况。

主要的标定步骤：

在角点提取完之后，就可以单击标定工具箱面板上的“Calibration

1. ”来运行主要的相机标定程序。

2.  

3. 标定主要通过两个步骤来完成：初次初始化以及非线性优化。

4. 初始化步骤中对标定参数进行闭环计算，这个过程不包括任何镜头畸变（程序名：init_calib_param.m）

5. 非线性优化过程中将对所有的标定参数最小化总体映射误差（从最小二乘的角度出发）（9个内参以及6X20=129、

6. 个外参）。优化是对特定雅可比矩阵进行计算然后往梯度下降的方向进行的。

1. 标定参数存储在一系列变量中。注意切向畸变系数和第6个径向畸变系数没有没有被估算（这是默认的模式）。因此

2. 在像素坐标中X和Y之间是90°。在大多数实际情况中，这是一个很理想化的设想。然而，接下来，将会讲述一种介绍

3. 在优化中切向畸变alpha_c的方法。

4.  

5. 从上图中我们可以注意到：为了达到最小值，只用了11次梯度迭代。这就意味着只有11次对映射函数、雅可比计算

6. 以及求逆的评估。快速收敛的一个原因就是初始化程序所要计算的参数的有一个好的初始预估值。

7. 现在，忽略推荐的可以减少畸变的模型的系统。对一个模型的复杂性进行判断的映射误差仍然很大。这主要是因为

8. 对于一些图像一些网格角点并没有被精确地提取。

9.  

10. 单击面板上的“Reproject on images”来将网格角点映射到原始图像中。这些映射是基于当前的内参和外参计算

11. 出来的。输入一个空字符（直接按"Enter"）作为“Number(s) of image(s) to show([]=all images)”来

12. 表示你想查看所有图像：

下面的图像显示了最初的四张检测到的角点的图像（红色的叉）以及映射的网格角点（圆）。

映射误差也以有颜色的叉叉显示在图中：

1. 为了退出误差分析工具，在图像上的任何位置右击（稍后你将会理解这个选项的使用）。

2.  

3. 在面板中单击“Show Extrinsic”。外参（棋盘格相对于相机的相对位置）就以3D的形式显示出来了：

1. 在上图中，坐标系（Oc,Xc,Yc,Zc）是相机的参考坐标系。红色的金字塔状的就是由图像平面定义的相机的有效

2. 视场。可以在相机坐标系视角或者世界坐标系视角之间切换：

1. 在这个视角里面，每个相机的位姿都用绿色的金字塔表示。

2.  

3. 现在我们回到前面的误差分析那一段，注意到在很多图像中的投影误差是非常大的。原因就是我们在一些高度畸变

4. 的图像的角点提取工作做得不到位。然而，我们现在可以通过对所有图像重新计算图像角点来进行矫正。接下来需要

5. 做的就是：单击面板中的“

Recomp. corners

1. ”按钮，然后再次选择角点检测器的窗口尺寸(wintx=winty=5这个

2. 默认值)。

1. 对于最后问题“Number(s) of image(s) to process”亦然输入“Enter”选择默认值去重新计算所有图像中的

2. 角点。然后就是选择角点提取的方式：自动和手动，自动的就是使用重新投影的网格作为角点的初始预估位置。手

3. 动的方式就需要使用者手动的提取角点。在现在这样的条件下，因为重投影的网格点非常接近实际的图像角点，因此

4. 我们选择自动的方式：直接“Enter”输入默认值。所有图像的角点就会被重新计算。你的matlab命令行窗口就会出

5. 现下面这种形式：

然后通过单击“Calibration”进行一次标定优化：

1. 可以注意到只需要6次迭代就收敛了，并且没有进行初始化过程（因为优化是在前面标定的结果之上进行的）。上图

2. 中的两个值0.12668和0.12604分别是X和Y方向像素上投影的标准差。注意到标定参数的不确定性也进行了估算。

3. 数值大概是标准差的3倍。

4.  

5. 优化之后，单击“Save”保存标定结果（内参和外参）到matlab文件“Calib_Results.mat”

我们再次单击“Reproject on images”将网格点投影到原始图像中。前四张图像如下图所示：

然后再“Analyse error”看看新的投影误差（可以看到误差比之前更小了）：

右击上面的误差图像（退出误差分析工具），单击“Show Extrinsic”看看棋盘格相对于相机的3D位置关系：

工具“Analyse error”允许你去检查哪个点对应大的误差。单击“Analyse error”并且选择图像由上角的那个点

单击选中之后，下面的信息就会出现在命令行窗口：

1. 这就意味着对应的点在第18张图像中，在标定板网格坐标的（0，0）的位置（标定板的原点）。下图是此点到原始

2. 图像的距离。

1. 误差检查工具对于在一张或多张图像中角点提取失败的情况下非常有用。在这种情况下，使用者可以使用不同的窗

2. 口尺寸去重新对于特定图像的角度进行重新计算。

3.  

4. 例如，我们使用窗口尺寸（wintx=winty=9）来对所有图像的角点进行计算，但对图像20我们使用(wintx=winty

5. =5）的窗口尺寸，对图像5，7，8，19我们采用（wintx=winty=7），图像18采用（wintx=winty=8）的窗口

6. 尺寸进行计算。角点的提取会调用三次“Recomp.corners”。第一次调用使用wintx=winty=9来处理图像1，2，

7. 3，4，6，9，10，11，12，13，14，15，16和17.然后选择自动模式：

第二次调用，使用wintx=winty=8来处理图像18，然后再次选择自动模式：

第三次调用，使用wintx=winty=7来处理图像5，7，8和19：

单击“Calibration”进行重新标定：

观察上面的投影误差（0.11689，0.11500）比前面的更小了。另外注意到，标定参数的不确定性也更小了。通过单击“Analyse error”来检测误差：

1. 让我们来看看前面那个兴趣图像18中的点，在标定板的网格坐标（0，0）处。单击“Reproject on images”然后

2. 选择只显示图像18（当然在此之前你必须右击误差分析图像退出误差分析工具）：

放大图像我们可以看到更小的投影误差：

单击“Save”保存标定结果到文件“Calib_Results.mat”中：

可以看到前面的标定结果已经被拷贝到文件“Calib_Results_old0.mat”中。

现在多加5张图像来重新进行相机标定。image21 image22 image23 image24 image25。然后“Read images”把所有的25张图像载入内存。然后以缩略图显示：

单击“Extract grid corners”来对新的5张图像进行角点提取，窗口尺寸用wintx=winty=5:

以传统的角度提取过程对这5张图像进行角点提取。然后单击“Calibration”运行又一次优化：

1. 接下来，使用不同的窗口尺寸对最后的四张图像进行重新计算。对图像22和24使wintx=winty=9，对图23使用

2. wintx=winty=8,对图像25使用wintx=winty=6。然后按照前面介绍的过程重新进行一次（三次调用“Recomp.corners

3. ”），重新计算之后，再次运行“Calibration”:

然后“Save”保存标定结果。

1. 作为练习，我们去除图像16，18，19，24和25然后重新进行标定：

2. 单击“

Add/Suppress images”

输入要去掉的图像([16 18 19 24 25]):

重新“Calibration”进行标定：

1. “Add/Supress images”取决于使用者是否需要某些图像。实际上，这个函数只是简单地更新active_image这个

2. 向量，使对应的图像索引为0或1.

3. 接下来，载入之前标定的结果“Load”：

1. 现在又回到了没有去掉图像之前的状态了。现在我们实现一次含有用来描述X和Y像素之间角度的切向因素alpha_c

2. 进行的标定。为此，我们需要将est_alpha设置为1(在命令行中进行)。As an exercise, let us fit the

3. radial distortion model up to the 6th order (up to now, it was up to the 4th order, with

4. tangential distortion). For that, set the last entry of the vector est_dist to one:

然后重新运行“Calibration”：

1. 优化之后可以看到，切向因素非常接近0（alpha_c=0.00042），这就意味着X和Y像素之间的角度非常接近90°

2. （89.976°）。这调整了之前的90°的设想。另外，注意到第6个径向畸变系数非常大。在这种情况下，我们最好

3. 就是不使用它的估算值。在这里，我们直接将est_dist最后一个量设置为0：

再次“Calibration”：

如果标定结果满意的话就“Save”保存标定结果。

1. 为了选择合理的畸变模型来使用，通常可视化对像素图像的畸变影响以及畸变的径向部分和切向部分

2. 的比对是非常有用的。为此，在matlab命令行运行

visualize_distortions，就会有三张图出来：

1. 第一幅图显示了整体的畸变模型对图像每个像素的影响。每个箭头表示由于镜头畸变而使一个像素发生的位移效果。

2. 可以看到图像角落处的像素移动了25个像素。第二幅图显示了畸变的切向部分。在这幅图中，最大的位移式0.14个

3. 像素，在图像的左上角。最后，第三幅图显示了畸变的径向部分的影响。这幅图和第一幅图有点相似。说明畸变的切

4. 向部分相对于整体模型来说可以忽略不计。在第三幅图中，十字叉表示了图像的中心，而圆表示光心所在的位置。

5.  

6. 现在我们来试验一下，当没有畸变的情况下标定会有什么结果。使Kc=[0;0;0;0;0],并且fc没有各向异性（使fc

7. 几个方向都相等）:

然后，运行一次优化“Calibration”：

1. 和预期一样，畸变系数向量Kc都是0，焦距各个方向都相当，fc1=fc2。在实际中，这种标定的模型是不推荐的：

2. 因为在没有各向异性的幸亏下去估算切向畸变是没有意义的。通常情况下，除非有特定的应用，一般推荐在模型中评

3. 估各向异性。对于畸变模型，一般经常只对其中一些系数进行优化。例如，将est_dist设置为【1；0；0；0】

4. 只对第一个畸变系数kc(1)进行估算而把其他三个畸变系数直接置0.这种模型也叫作第二对称性径向畸变模型。它

5. 是一个非常可行的模型，尤其是当使用比较低的畸变光学系统（昂贵的镜头），或者当用来标定的图像很少的时候。

6. 另一个比较常用的畸变模型是第4对称性径向畸变模型而没有切向部分畸变（est_dist=[1;1;0;0]）。这个模

7. 型被zhang使用并被调整了，基于现在大多的镜头制造在聚焦方面都没有缺陷。这个模型可以很好地用于现在这个

8. 例子中，从前面三个图也可以看出，这个镜头的切向部分畸变远小于径向部分畸变。

9.  

10. 最后，让我们来做一次，没有各向异性fc(2)/fc(1)，光心cc,畸变系数kc，切向系数alpha_c的优化。为此

一般地，如果光心没有被估算，则最好的预估值就是图像的中心：

然后运行“Calibration”：

1. 从上面可以看到，光心cc优化后还在图像的中心（因为center_optim=0）

2.  

3. 接下来，载入原来的标定结果：

标定工具箱的其他功能

仅仅计算外参：

1. 我们可以只计算图像的外参，而内参直接用之前标定好的结果，在前面标定好的基础上，输入一张图像，然后在面板

2. 上“Comp.Extrinsic”，就可以在matlab的命令行中出现下面的情况：

1. 外参在Rc_ext和Tc_ext两个变量中，另外一个变量omc_ext和Rc_ext一个效果，可以将omc_ext用罗得里格斯

2. 变换进行转换Rc_ext=rodrigues(omc_ext)。

图像矫正

1. 这个函数帮助你利用之前标定的内参得到一些没有畸变的图像。

2.  

3. 作为一个练习，我们来对图像20进行矫正。

4. 在面板中单击“

Undistort image”：

输入1来选择一张要矫正的图像，注意不要输入图像的扩展名，只输入Image20就可以，然后是图像的类型。

初始图像存储在矩阵I中，如下图所示：

矫正过的图像存储在矩阵I2中，如下图所示：

1. 新产生的矫正的图像也存储成Image20_rect.tif。

2.  

3. 现在我们来矫正所有的图像。“Undistort image”，然后对第一个问题输入空参数。然后所有的标定图像都将被

4. 矫正，然后存储为Image_rect1.tif,Image_rect2.tif...

1. 也可以将标定数据导出为其他格式的数据：这样当你使用同样的数据来做标定，然后进行对比的时候是非常有用的

2. 这个可以在角点提取阶段使用，单击“Export calib data”：

输入0选择使用Willson Heikkil格式，输入数据名（shot），然后每张图像的标定数据就会被保存为shot1，shot2,...

1. 也可以导出为zhang的格式。“Export calib data”，然后输入1.然后输入两个文件基名：一个是3D模型坐标（Model），

2. 另一个是图像坐标（data）。然后程序会创建一系列的text（Model1.txt,data1.txt,...），可以被zhang的

3. 代码直接使用：

2. 双目标定

双目视觉系统标定、双目图像校正

 

这个例子介绍如何使用工具箱进行立体视觉系统标定，包括内外参数，以及用获得的数据进行立体校正和三维测量。

 

1、下载双目示例图片，包括14对左右摄像头获取的图像，还有两个独立标定的结果。

 

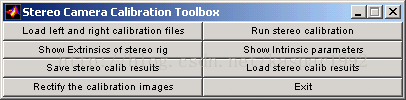
2、在窗口中输入stereo_gui ,出现工具窗口

 

 

3、点击第一个按钮 Load left and right calibration files . 窗口提示输入左右标定文件名，分别输入对应文件名 Calib_Results_left.mat  Calib_Results_right.mat 

 

 

 

4、内部参数的初始值在窗口中显示，并估算出外部参数 om 和 T ，右相机相对左相机的平移和旋转。3*3旋转矩阵是 om 通过 rodrigues 求出 。

 

 

 

然后运行全局双目优化算法通过点击按钮Run stereo calibration 有以下所示结果

 

 

 

可以发现内外参数都被重新计算，所有未确定的参数也确定保证误差最小的基础上。你会发现不确定的内参数都变小了，这是因为最优化算法的作用。默认情况下，优化算法

 

会重新计算左右相机的内部参数，但是如果你不想让其优化，则在窗口运行 recompute_instrinsic_left 和或者recompute_instrinsic_right .

 

在窗口输入help go_calib_stereo 查看更多信息.

 

5、点击 Save stereo calib results ,存储标定数据结果

 

 

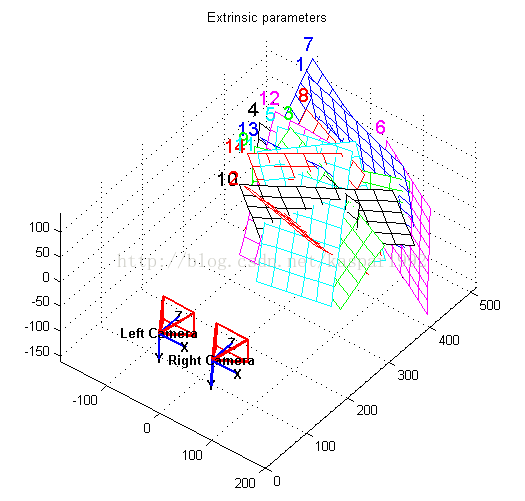
6、双目相机的空间位置和标定平面可以可视化，通过点击按键 Show Extrinsics of the rig.

 

 

7、校正图像

 

点击 Rectify the calibration images ，所有14对图片校正后图像存储在文件下。