Python求凸包及多边形面积

一般有两种算法来计算平面上给定n个点的凸包：Graham扫描法(Graham’s scan)，时间复杂度为O(nlgn)；Jarvis步进法(Jarvis march)，时间复杂度为O(nh)，其中h为凸包顶点的个数。这两种算法都按逆时针方向输出凸包顶点。

Graham扫描法

用一个栈来解决凸包问题，点集Q中每个点都会进栈一次，不符合条件的点会被弹出，算法终止时，栈中的点就是凸包的顶点(逆时针顺序在边界上)。

算法步骤如下图：

import sys
import math
import time
import random

#获取基准点的下标,基准点是p[k]
def get_leftbottompoint(p):
    k = 0
    for i in range(1, len(p)):
        if p[i][1] < p[k][1] or (p[i][1] == p[k][1] and p[i][0] < p[k][0]):
            k = i
    return k

#叉乘计算方法
def multiply(p1, p2, p0):
    return (p1[0] - p0[0]) * (p2[1] - p0[1]) - (p2[0] - p0[0]) * (p1[1] - p0[1])

#获取极角，通过求反正切得出，考虑pi/2的情况
def get_arc(p1, p0):
    # 兼容sort_points_tan的考虑
    if (p1[0] - p0[0]) == 0:
        if ((p1[1] - p0[1])) == 0:
            return -1;
        else:
            return math.pi / 2
    tan = float((p1[1] - p0[1])) / float((p1[0] - p0[0]))
    arc = math.atan(tan)
    if arc >= 0:
        return arc
    else:
        return math.pi + arc

#对极角进行排序,排序结果list不包含基准点
def sort_points_tan(p, pk):
    p2 = []
    for i in range(0, len(p)):
        p2.append({"index": i, "arc": get_arc(p[i], pk)})
    #print('排序前:',p2)
    p2.sort(key=lambda k: (k.get('arc')))
    #print('排序后:',p2)
    p_out = []
    for i in range(0, len(p2)):
        p_out.append(p[p2[i]["index"]])
    return p_out

def convex_hull(p):
    p=list(set(p))
    #print('全部点:',p)
    k = get_leftbottompoint(p)
    pk = p[k]
    p.remove(p[k])
    #print('排序前去除基准点的所有点:',p,'基准点:',pk)

    p_sort = sort_points_tan(p, pk)   #按与基准点连线和x轴正向的夹角排序后的点坐标
    #print('其余点与基准点夹角排序:',p_sort)
    p_result = [pk,p_sort[0]]

    top = 2
    for i in range(1, len(p_sort)):
        #####################################
        #叉乘为正,向前递归删点;叉乘为负,序列追加新点
        while(multiply(p_result[-2], p_sort[i],p_result[-1]) > 0):
            p_result.pop()
        p_result.append(p_sort[i])    
    return p_result#测试

if __name__ == '__main__':
    pass
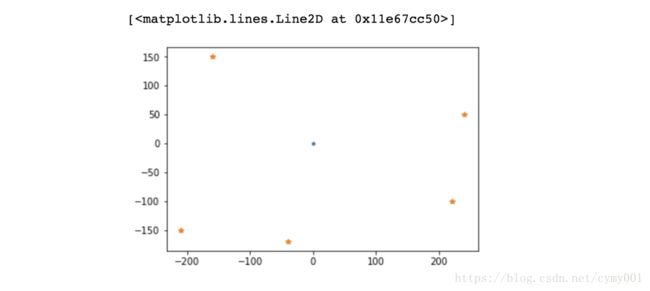
    test_data = [(220, -100), (0,0), (-40, -170), (240, 50), (-160, 150), (-210, -150)]
    print(test_data)

    result = convex_hull(test_data)
    print(result)
    t=0

import matplotlib.pyplot as plt
x1=[]
y1=[]
for i in range(len(test_data)):
    ri=test_data[i]
    #print(ri)
    x1.append(ri[0])
    y1.append(ri[1])

plt.plot(x1,y1,linestyle=' ',marker='.')


xx=[]
yy=[]
for i in range(len(result)):
    ri=result[i]
    #print(ri)
    xx.append(ri[0])
    yy.append(ri[1])

plt.plot(xx,yy,linestyle=' ',marker='*')

计算多边形面积

（1）顺时针给定构成凸包的n个点坐标，叉乘法求多边形面积：

def GetAreaOfPolyGonbyVector(points):
    # 基于向量叉乘计算多边形面积
    area = 0
    if(len(points)<3):
        raise Exception("error")

    for i in range(0,len(points)-1):
        p1 = points[i]
        p2 = points[i + 1]

        triArea = (p1[0]*p2[1] - p2[0]*p1[1])/2
        #print(triArea)
        area += triArea

    fn=(points[-1][0]*points[0][1]-points[0][0]*points[-1][1])/2
    #print(fn)
    return abs(area+fn)

points = []
x = [1,3,2]
y = [1,2,2] 
#[(1,1),(3,1),(5,3),(3,5),(1,3)] 
# x=[1,3,5,3,1]
# y=[1,1,3,5,3]
for index in range(len(x)):
    points.append((x[index],y[index]))
area = GetAreaOfPolyGonbyVector(points)
print(area)
#print(math.ceil(area))

（2）顺时针给定构成凸包的n个点经纬度坐标，先将经纬度坐标转化成凸多边形的边的经纬度距离，利用海伦公式求多边形面积：

from geopy.distance import vincenty
import math
def HeronGetAreaOfPolyGonbyVector(points):
    # 基于海伦公式计算多边形面积
    area = 0
    if(len(points)<3):
        raise Exception("error")

    pb=((points[-1][0]+points[0][0])/2,(points[-1][1]+points[0][1])/2)   #基准点选为第一个点和最后一个点连线边上的中点

    for i in range(0,len(points)-1):
        p1 = points[i]
        p2 = points[i + 1]

        db1 = vincenty(pb,p1).meters   #根据维度转化成经纬度距离
        d12 = vincenty(p1,p2).meters
        d2b = vincenty(p2,pb).meters
        #print(db1,d12,d2b)

        hc = (db1+d12+d2b)/2   #db1是基准点和p1的距离，d12是p1和p2的距离，d2b是p2和基准点距离
        #print(hc, hc-db1, hc-d12, hc-d2b)
        triArea = math.sqrt(hc*(hc-db1)*(hc-d12)*(hc-d2b)) 
        #print(triArea)
        area += triArea

    return area


points = []
x = [1,3,2]
y = [1,2,2] 
#[(1,1),(3,1),(5,3),(3,5),(1,3)] 
# x=[1,3,5,3,1]
# y=[1,1,3,5,3]
for index in range(len(x)):
    points.append((x[index],y[index]))

area = HeronGetAreaOfPolyGonbyVector(points)
print(area)
#print(math.ceil(area))

Graham程序原理

（1）基准点的确认原则：
有唯一的某个点纵坐标最小，该点为基准点；
不止一个点的纵坐标最小，选这些点里最靠左的为基准点

（2）计算叉乘【后续利用叉乘正负判断夹角是否大于 180o 180 o 】：

p1x⋅p2y−p2x⋅p1y=∣∣∣∣p1xp2xp1yp2y∣∣∣∣=(p1x,p1y)×(p2x,p2y) p 1 x ⋅ p 2 y − p 2 x ⋅ p 1 y = | p 1 x p 1 y p 2 x p 2 y | = ( p 1 x , p 1 y ) × ( p 2 x , p 2 y )

（3）获取极角，通过求反正切得出：
若横纵坐标都相等(两点相同)，返回-1；
若横坐标相等/纵坐标不相等(两点连线垂直y轴)，返回 π2 π 2 ；
若横坐标不相等，计算 tanθ=p1y−p0yp1x−p0x t a n θ = p 1 y − p 0 y p 1 x − p 0 x ，则 θ=arctan(p1y−p0yp1x−p0x) θ = a r c t a n ( p 1 y − p 0 y p 1 x − p 0 x ) ，若 θ≥0 θ ≥ 0 ，返回 θ θ ；若 θ<0 θ < 0 ，返回 π−θ π − θ 【结合反正切的主值区间考虑】

（4）对极角进行排序，排序结果list不包含基准点：

p2=[{"index":0, "arc":get_arc(p[0],p[k])}，
    {"index":1, "arc":get_arc(p[1],p[k])}，
    ···
    {"index":k-1, "arc":get_arc(p[k-1],p[k])}，
    {"index":k+1, "arc":get_arc(p[k+1],p[k])}，
    ···
    {"index":n, "arc":get_arc(p[n],p[k])}]
#get_arc(p[0],p[k])即获得p[0]点与基准点p[k]连线的极角(与x轴正向夹角)
#根据p2的“arc”键的值从小到大排序，最后输出按该角度值排序对应顺序的各个点

（5）逆时针确定凸多边形：

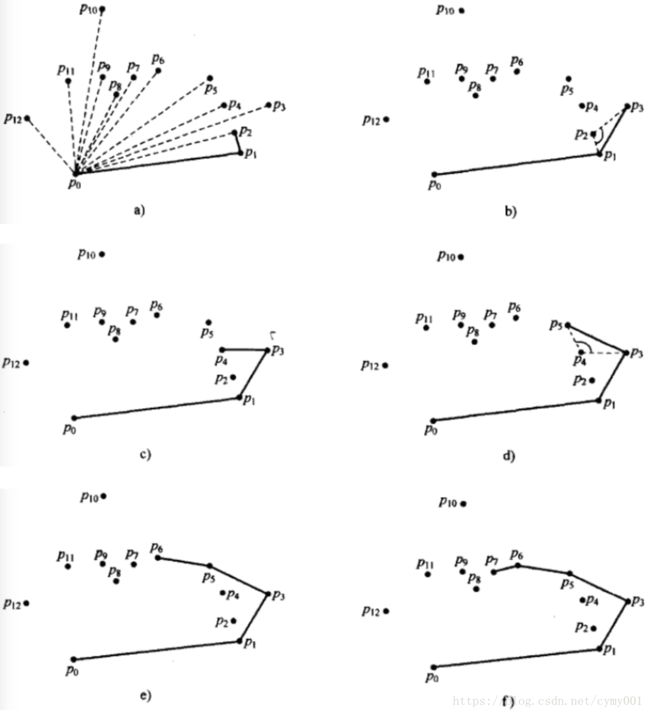
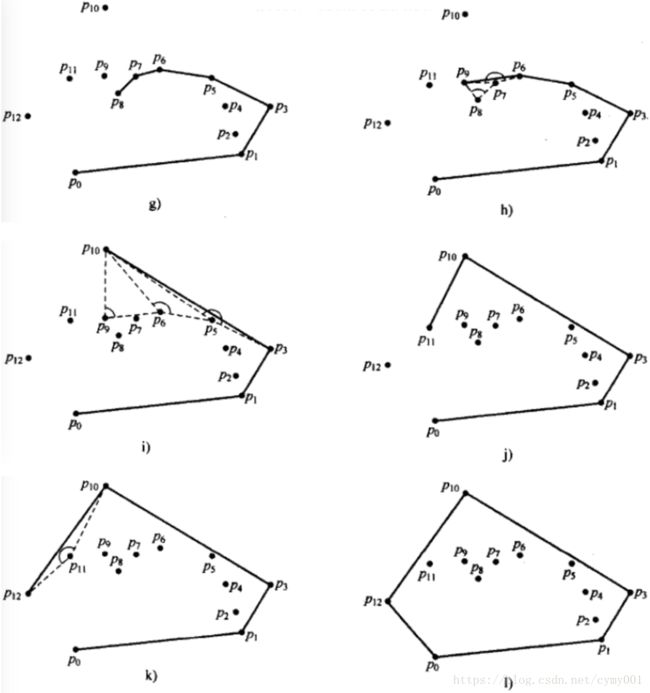
主要是找角度是否大于 180o 180 o ——差乘正负——点进出栈顺序三者关系
注意差乘函数：multiply(p1,p2,p0)=(p1−p0)×(p2−p0) 注 意 差 乘 函 数 ： m u l t i p l y ( p 1 , p 2 , p 0 ) = ( p 1 − p 0 ) × ( p 2 − p 0 )
加p_3：
p2p1×p2p3=(p1−p2)×(p3−p2)=multiply(p1,p3,p2)>0，夹角小于180o，删p2，栈内p0,p1,p3 p 2 p 1 × p 2 p 3 = ( p 1 − p 2 ) × ( p 3 − p 2 ) = m u l t i p l y ( p 1 , p 3 , p 2 ) > 0 ， 夹 角 小 于 180 o ， 删 p 2 ， 栈 内 p 0 , p 1 , p 3
加p_4：
p3p1×p3p4=(p1−p3)×(p4−p3)=multiply(p1,p4,p3)<0，夹角大于180o，留p3，栈内p0,p1,p3,p4 p 3 p 1 × p 3 p 4 = ( p 1 − p 3 ) × ( p 4 − p 3 ) = m u l t i p l y ( p 1 , p 4 , p 3 ) < 0 ， 夹 角 大 于 180 o ， 留 p 3 ， 栈 内 p 0 , p 1 , p 3 , p 4
加p_5：
p4p3×p4p5=(p3−p4)×(p5−p4)=multiply(p3,p5,p4)>0，夹角大于180o，删p4，栈内p0,p1,p3,p5 p 4 p 3 × p 4 p 5 = ( p 3 − p 4 ) × ( p 5 − p 4 ) = m u l t i p l y ( p 3 , p 5 , p 4 ) > 0 ， 夹 角 大 于 180 o ， 删 p 4 ， 栈 内 p 0 , p 1 , p 3 , p 5
加p_6：
p5p3×p5p6=(p3−p5)×(p6−p5)=multiply(p3,p6,p5)<0，夹角大于180o，留p5，栈内p0,p1,p3,p5,p6 p 5 p 3 × p 5 p 6 = ( p 3 − p 5 ) × ( p 6 − p 5 ) = m u l t i p l y ( p 3 , p 6 , p 5 ) < 0 ， 夹 角 大 于 180 o ， 留 p 5 ， 栈 内 p 0 , p 1 , p 3 , p 5 , p 6
加p_7：
p6p5×p6p7=(p5−p6)×(p7−p6)=multiply(p5,p7,p6)<0，夹角大于180o，留p6，栈内p0,p1,p3,p5,p6,p7 p 6 p 5 × p 6 p 7 = ( p 5 − p 6 ) × ( p 7 − p 6 ) = m u l t i p l y ( p 5 , p 7 , p 6 ) < 0 ， 夹 角 大 于 180 o ， 留 p 6 ， 栈 内 p 0 , p 1 , p 3 , p 5 , p 6 , p 7
加p_8：
p7p6×p7p8=(p6−p7)×(p8−p7)=multiply(p6,p8,p7)<0，夹角大于180o，留p7，栈内p0,p1,p3,p5,p6,p7,p8 p 7 p 6 × p 7 p 8 = ( p 6 − p 7 ) × ( p 8 − p 7 ) = m u l t i p l y ( p 6 , p 8 , p 7 ) < 0 ， 夹 角 大 于 180 o ， 留 p 7 ， 栈 内 p 0 , p 1 , p 3 , p 5 , p 6 , p 7 , p 8
加p_9：
p8p7×p8p9=(p7−p8)×(p9−p8)=multiply(p7,p9,p8)>0，夹角小于180o，删p8，栈内p0,p1,p3,p5,p6,p7 p 8 p 7 × p 8 p 9 = ( p 7 − p 8 ) × ( p 9 − p 8 ) = m u l t i p l y ( p 7 , p 9 , p 8 ) > 0 ， 夹 角 小 于 180 o ， 删 p 8 ， 栈 内 p 0 , p 1 , p 3 , p 5 , p 6 , p 7
p7p6×p7p9=(p6−p7)×(p9−p7)=multiply(p6,p9,p7)<0，夹角小于180o，删p7，栈内p0,p1,p3,p5,p6 p 7 p 6 × p 7 p 9 = ( p 6 − p 7 ) × ( p 9 − p 7 ) = m u l t i p l y ( p 6 , p 9 , p 7 ) < 0 ， 夹 角 小 于 180 o ， 删 p 7 ， 栈 内 p 0 , p 1 , p 3 , p 5 , p 6
p6p5×p6p9=(p5−p6)×(p9−p6)=multiply(p5,p9,p6)<0，夹角小于180o，删p6，栈内p0,p1,p3,p5 p 6 p 5 × p 6 p 9 = ( p 5 − p 6 ) × ( p 9 − p 6 ) = m u l t i p l y ( p 5 , p 9 , p 6 ) < 0 ， 夹 角 小 于 180 o ， 删 p 6 ， 栈 内 p 0 , p 1 , p 3 , p 5
p5p3×p5p9=(p3−p5)×(p9−p5)=multiply(p3,p9,p5)<0，夹角小于180o，删p5，栈内p0,p1,p3 p 5 p 3 × p 5 p 9 = ( p 3 − p 5 ) × ( p 9 − p 5 ) = m u l t i p l y ( p 3 , p 9 , p 5 ) < 0 ， 夹 角 小 于 180 o ， 删 p 5 ， 栈 内 p 0 , p 1 , p 3
p3p1×p3p9=(p1−p3)×(p9−p3)=multiply(p1,p9,p3)<0，夹角大于180o，留p3，栈内p0,p1,p3,p9 p 3 p 1 × p 3 p 9 = ( p 1 − p 3 ) × ( p 9 − p 3 ) = m u l t i p l y ( p 1 , p 9 , p 3 ) < 0 ， 夹 角 大 于 180 o ， 留 p 3 ， 栈 内 p 0 , p 1 , p 3 , p 9
...一直遍历到最后一个点 . . . 一 直 遍 历 到 最 后 一 个 点
规律： 叉乘>0，夹角小于180o，递归向前删点；叉乘<0，夹角大于180o，不删点，加入新点，向后遍历 叉 乘 > 0 ， 夹 角 小 于 180 o ， 递 归 向 前 删 点 ； 叉 乘 < 0 ， 夹 角 大 于 180 o ， 不 删 点 ， 加 入 新 点 ， 向 后 遍 历
注意：（a）上述给非基准点按极角从到大小排号时，有两个及以上点“和基准点连线构成的极角”相等时，这些点的排号挨着但是没有固定顺序，这点并不影响算法给出凸包的准确性。（b）对排号最后的一个点，扫描算法里没有任何删除该点的机制，但是这点也不影响算法给出凸包的准确性。（c）上述程序需要额外加入，判断结束栈内点数小于3和筛选凸包前点数小于3，不能计算多边形面积的情况，可以直接给这种情况赋值0返回。