百练/ 北京大学2016研究生推免上机考试(校外)H: Tree Summing(栈)
题目来源:http://qwsfsx.openjudge.cn/level3/1145/
1145:TreeSumming
总时间限制: 1000ms 内存限制: 65536kB
描述
LISPwas one of the earliest high-level programming languages and, with FORTRAN, isone of the oldest languages currently being used. Lists, which are thefundamental data structures in LISP, can easily be adapted to represent otherimportant data structures such as trees.
This problem deals with determining whether binary trees represented as LISPS-expressions possess a certain property.
Given a binary tree of integers, you are to write a program that determineswhether there exists a root-to-leaf path whose nodes sum to a specifiedinteger. For example, in the tree shown below there are exactly fourroot-to-leaf paths. The sums of the paths are 27, 22, 26, and 18.
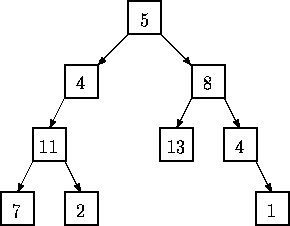
Binary trees are represented in the input file as LISP S-expressions having thefollowing form.
empty tree ::= ()
tree ::= empty tree (integer tree tree)
The tree diagrammed above is represented by the expression (5 (4 (11 (7 () ())(2 () ()) ) ()) (8 (13 () ()) (4 () (1 () ()) ) ) )
Note that with this formulation all leaves of a tree are of the form (integer() () )
Since an empty tree has no root-to-leaf paths, any query as to whether a pathexists whose sum is a specified integer in an empty tree must be answerednegatively.
输入
Theinput consists of a sequence of test cases in the form of integer/tree pairs.Each test case consists of an integer followed by one or more spaces followedby a binary tree formatted as an S-expression as described above. All binarytree S-expressions will be valid, but expressions may be spread over severallines and may contain spaces. There will be one or more test cases in an inputfile, and input is terminated by end-of-file.
输出
Thereshould be one line of output for each test case (integer/tree pair) in theinput file. For each pair I,T (I represents the integer, T represents the tree)the output is the string yes if there is a root-to-leaf path in T whose sum isI and no if there is no path in T whose sum is I.
样例输入
22 (5(4(11(7()())(2()()))()) (8(13()())(4()(1()()))))
20 (5(4(11(7()())(2()()))()) (8(13()())(4()(1()()))))
10 (3
(2 (4 () () )
(8 () () ) )
(1 (6 () () )
(4 () () ) ) )
5 ()
样例输出
yes
no
yes
no
-----------------------------------------------------
解题思路
括号匹配,栈的应用
逐个字符读入,注意数字可能有负的
-----------------------------------------------------
代码
//H:Tree Summing
//总时间限制: 1000ms 内存限制: 65536kB
//描述
//LISP was one of the earliest high-level programming languages and, with FORTRAN, is one of the oldest languages currently being used. Lists, which are the fundamental data structures in LISP, can easily be adapted to represent other important data structures such as trees.
//
//This problem deals with determining whether binary trees represented as LISP S-expressions possess a certain property.
//Given a binary tree of integers, you are to write a program that determines whether there exists a root-to-leaf path whose nodes sum to a specified integer. For example, in the tree shown below there are exactly four root-to-leaf paths. The sums of the paths are 27, 22, 26, and 18.
//
//
//Binary trees are represented in the input file as LISP S-expressions having the following form.
//
//empty tree ::= ()
//
//tree ::= empty tree (integer tree tree)
//
//The tree diagrammed above is represented by the expression (5 (4 (11 (7 () ()) (2 () ()) ) ()) (8 (13 () ()) (4 () (1 () ()) ) ) )
//
//Note that with this formulation all leaves of a tree are of the form (integer () () )
//
//Since an empty tree has no root-to-leaf paths, any query as to whether a path exists whose sum is a specified integer in an empty tree must be answered negatively.
//输入
//The input consists of a sequence of test cases in the form of integer/tree pairs. Each test case consists of an integer followed by one or more spaces followed by a binary tree formatted as an S-expression as described above. All binary tree S-expressions will be valid, but expressions may be spread over several lines and may contain spaces. There will be one or more test cases in an input file, and input is terminated by end-of-file.
//输出
//There should be one line of output for each test case (integer/tree pair) in the input file. For each pair I,T (I represents the integer, T represents the tree) the output is the string yes if there is a root-to-leaf path in T whose sum is I and no if there is no path in T whose sum is I.
//样例输入
//22 (5(4(11(7()())(2()()))()) (8(13()())(4()(1()()))))
//20 (5(4(11(7()())(2()()))()) (8(13()())(4()(1()()))))
//10 (3
// (2 (4 () () )
// (8 () () ) )
// (1 (6 () () )
// (4 () () ) ) )
//5 ()
//样例输出
//yes
//no
//yes
//no
#include
#include
#include
using namespace std;
int main()
{
#ifndef ONLINE_JUDGE
ifstream fin("tm201602H.txt");
vector mystack;
int i = 0, sum = 0, tmpsum = 0, tmp = 0, kuohao = 0;
// sum: 这棵树对应的sum, tmpsum: 当前树的路径和,tmp: 当前数据的绝对值
// kuohao: 左括号的个数,决定遇到右括号的时候mystack中要不要出栈
bool negative = false, yes = false; // negative: 是否是负数, yes: true输出yes, false输出false
short leaf = 0; // leaf=2, 是叶子节点,需要计算
char dest; // 当前接收到的字符
while (fin >> dest)
{
if (dest == '(' && kuohao==0)// 没有左括号的时候tmp就是sum
{
if (negative)
{
tmp *= -1;
}
sum = tmp;
tmpsum = 0;
tmp = 0;
negative = false;
yes = false;
kuohao = 1;
}
else if (dest == '(') // 已有左括号时将tmp入栈
{
if (tmp) // 如果tmp不是0
{
if (negative)
{
tmp *= -1;
}
mystack.push_back(tmp);
tmp = 0;
negative = false;
}
kuohao++;
}
else if (dest == ')' && mystack.size()==kuohao)// 匹配到有内容的左括号
{
mystack.pop_back();
kuohao--;
if (kuohao == 0)
{
if (yes)
{
cout << "yes" << endl;
}
else
{
cout << "no" << endl;
}
}
leaf = 0;
}
else if (dest == ')') // 匹配到空的左括号
{
kuohao--;
if (kuohao == 0)
{
if (yes)
{
cout << "yes" << endl;
}
else
{
cout << "no" < mystack;
int i = 0, sum = 0, tmpsum = 0, tmp = 0, kuohao = 0;
// sum: 这棵树对应的sum, tmpsum: 当前树的路径和,tmp: 当前数据的绝对值
// kuohao: 左括号的个数,决定遇到右括号的时候mystack中要不要出栈
bool negative = false, yes = false; // negative: 是否是负数, yes: true输出yes, false输出false
short leaf = 0; // leaf=2, 是叶子节点,需要计算
char dest; // 当前接收到的字符
while (cin >> dest)
{
if (dest == '(' && kuohao==0)// 没有左括号的时候tmp就是sum
{
if (negative)
{
tmp *= -1;
}
sum = tmp;
tmpsum = 0;
tmp = 0;
negative = false;
yes = false;
kuohao = 1;
}
else if (dest == '(') // 已有左括号时将tmp入栈
{
if (tmp) // 如果tmp不是0
{
if (negative)
{
tmp *= -1;
}
mystack.push_back(tmp);
tmp = 0;
negative = false;
}
kuohao++;
}
else if (dest == ')' && mystack.size()==kuohao)// 匹配到有内容的左括号
{
mystack.pop_back();
kuohao--;
if (kuohao == 0)
{
if (yes)
{
cout << "yes" << endl;
}
else
{
cout << "no" << endl;
}
}
leaf = 0;
}
else if (dest == ')') // 匹配到空的左括号
{
kuohao--;
if (kuohao == 0)
{
if (yes)
{
cout << "yes" << endl;
}
else
{
cout << "no" <