激励函数-Activation Funciton

一、什么是激励函数

　　激励函数一般用于神经网络的层与层之间，上一层的输出通过激励函数的转换之后输入到下一层中。神经网络模型是非线性的，如果没有使用激励函数，那么每一层实际上都相当于矩阵相乘。经过非线性的激励函数作用，使得神经网络有了更多的表现力。

　　为了更具体的描述这个问题，请参考知乎上的回答。

原文链接：https://www.zhihu.com/question/22334626/answer/103835591
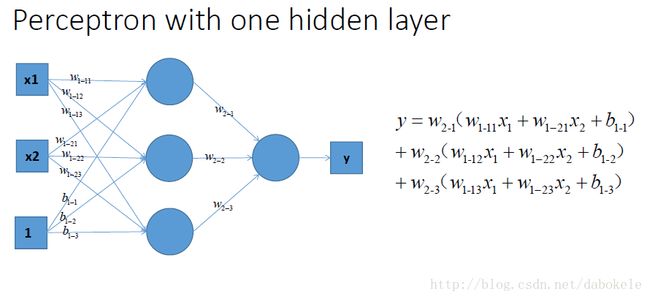
这是一个单层的感知机, 也是我们最常用的神经网络组成单元啦. 用它可以划出一条线, 把平面分割开

那么很容易地我们就会想用多个感知机来进行组合, 获得更强的分类能力, 这是没问题的啦~~
如图所示,

那么我们动笔算一算, 就可以发现, 这样一个神经网络组合起来,输出的时候无论如何都还是一个线性方程哎~纳尼, 说好的非线性分类呢~!!!!???

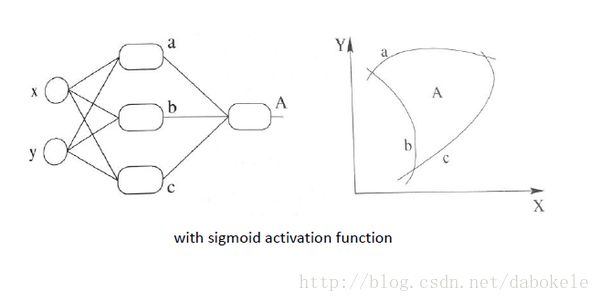
再盗用一幅经常在课堂上用的图…然而我已经不知道出处是哪了, 好像好多老师都是直接用的, 那我就不客气了嘿嘿嘿~，这幅图就跟前面的图一样, 描述了当我们直接使用step activation function的时候所能获得的分类器, 其实只能还是线性的, 最多不过是复杂的线性组合罢了，当然你可以说我们可以用无限条直线去逼近一条曲线啊……额,当然可以, 不过比起用non-linear的activation function来说就太傻了嘛….

祭出主菜. 题主问的激励函数作用是什么, 就在这里了!!
我们在每一层叠加完了以后, 加一个激活函数, 如图中的 y=δ(a) . 这样输出的就是一个不折不扣的非线性函数!

于是就很容易拓展到多层的情况啦, 更刚刚一样的结构, 加上non-linear activation function之后, 输出就变成了一个复杂的, 复杂的, 超级复杂的函数….额别问我他会长成什么样, 没人知道的~我们只能说, 有了这样的非线性激活函数以后, 神经网络的表达能力更加强大了~(比起纯线性组合, 那是必须得啊!)

继续厚颜无耻地放一张跟之前那副图并列的图, 加上非线性激活函数之后, 我们就有可能学习到这样的平滑分类平面. 这个比刚刚那个看起来牛逼多了有木有!

二、不同激励函数的公式和图形

1、Sigmoid函数
　　Sigmoid函数公式如下

δ(x)=11+e−x

　　函数图形如下：
　　
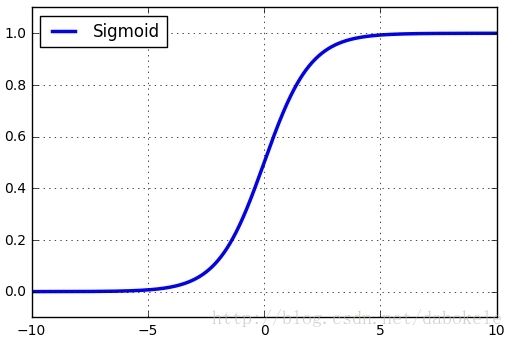
　　观察函数图形可以看到，Sigmoid函数将输入值归一化到 (0, 1)之间。
　　
　　Sigmoid函数导数公式如下

dδ(x)dx=ex(1+ex)2

　　函数图形如下：
　　

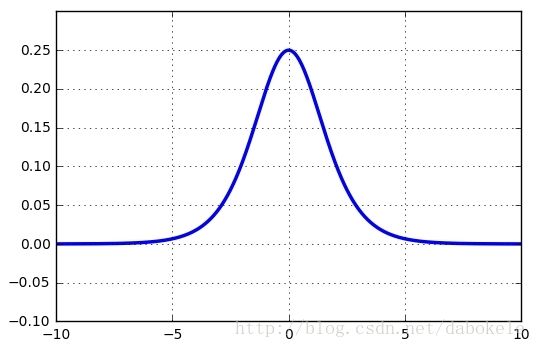
　　Sigmoid函数有三个缺点：　　
（1）Saturated neurons “kill” the gradients
　　在一些误差反向传播的场景下。首先会计算输出层的loss，然后将该loss以导数的形式不断向上一层神经网络传递，调整参数。使用Sigmoid函数的话，很容易导致loss导数变为0，从而失去优化参数的功能。
　　并且Sigmoid函数的导数最大值为0.25，该误差经过多层神经网络后，会快速衰减到0。
　　
（2）Sigmoid outputs are not zero-centered
　　Sigmoid函数的输出值恒大于零，那么下一层神经网络的输入x恒大于零。
　　

f=wTx+b

　　对上面这个公式来说， w上的gradient将会全部大于零或者全部小于零。这会导致模型训练的收敛速度变慢。
　　如下图所示，当输入值均为正数时，会导致按红色箭头所示的阶梯式更新。
　　
　　

（3）exp() is a bit compute expensive
　　最后，Sigmoid函数中的指数运算也是一个比较消耗计算资源的过程。
　　
2、Tanh函数

　　接下来的Tanh函数基于Sigmoid函数进行了一些优化，克服了Sigmoid的not zero-centered的缺点。Tanh函数公式如下：　　

tanh(x)=ex−e−xex+e−x

　　Sigmoid函数和Tanh函数之间的关系如下：

tanh(x)=2δ(2x)−1

　　
　　所以，对应于sigmoid的取值范围(0, 1)，tanh的取值范围为(0, 1)。将两个函数图像画在同一坐标系中，如下图所示：
　　

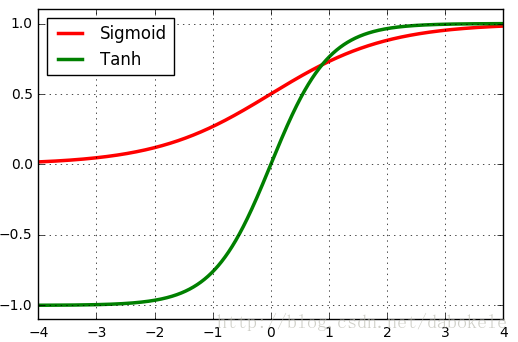
　　所以Tanh仍然具有Sigmoid函数的另外两个不足。
　　
3、ReLU函数
　　ReLU函数公式如下所示：

ReLU=max(0,x)

　　对应函数图形如下：
　　

　　该函数在输入小于0时输出值恒为0，在输入大于0时，输出线性增长。

　　ReLU函数没有Sigmoid函数及Tanh函数中的指数运算，并且也没有”kill” gradients的现象。
　　但是ReLU函数也有以下几个不足之处：
（1）not zero-centered
　　这个与Sigmoid类似，从函数图形就可以看出。
　　
（2）dead relu
　　这里指的是某些神经元可能永远不会被激活，导致对应的参数永远不会被更新。
　　比如说一个非常大的Gradient流过ReLU神经元，可能会导致参数更新后该神经元再也不会被激活。
　　当学习率过大时，可能会导致大部分神经元出现dead状况。所以使用该激活函数时应该避免学习率设置的过大。另外一种比较少见的情况是，某些初始化参数也会导致一些神经元出现dead状况。

　　以上部分参考自：http://mp.weixin.qq.com/s?__biz=MzI1NTE4NTUwOQ==&mid=2650324989&idx=2&sn=c70ec361350fefc7693d2231879dfd49&scene=0#wechat_redirect

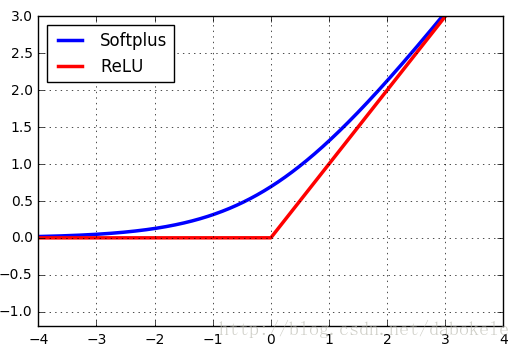
４、Softplus函数

　　Softplus函数公式如下，

Softplus(x)=log(1+ex)

　　通过观察该公式可以发现Softplus函数是Sigmoid函数的原函数。

　　Softplus函数与ReLU函数的图形对比如下图所示，
　　

　　在这里之所以将Softplus函数与ReLU函数的图形放在一起进行比较，是因为Softplus函数可以看成是ReLU函数的平滑版本。
　　并且，Softplus函数是对全部数据进行了非线性映射，是一种不饱和的非线性函数其表达式如公式，Softplus函数不具备稀疏表达的能力，收敛速度比ReLUs函数要慢很多。但该函数连续可微并且变化平缓，比Sigmoid函数更加接近生物学的激活特性，同时解决了Sigmoid函数的假饱和现象，易于网络训练和泛化性能的提高。虽然该函数的表达性能更优于ReLU函数和Sigmoid函数，即精确度相对于后者有所提高，但是其并没有加速神经网络的学习速度。
　　
５、Softsign函数
softsign(x)=11+|x|

　　

三、Tensorflow中提供的激励函数

　　在Tensorflow r1.0中提供了以下几种激励函数，其中包括连续非线性的（比如sigmoid, tanh, elu, softplus, softsign），连续但是并不是处处可微分的（relu, relu6, crelu, relu_x）以及随机函数（dropout）。

tf.nn.relu
tf.nn.relu6
tf.nn.crelu
tf.nn.elu
tf.nn.softplus
tf.nn.softsign
tf.nn.dropout
tf.nn.bias_add
tf.sigmoid
tf.tanh