数据结构----关键路径详解(Java)

算法说明：

求关键路径
1.输入e条弧，建立AOE网的存储结构，顶点数为n，顶点从0开始编号，设源点为v0、汇点为vn-1
2.从源点v0出发，令ve[0]=0，按拓扑有序求其余各顶点事件的最早发生时间ve[i](1≤i≤n-1)。如果得到的拓扑有序序列中顶点个数小于网中的顶点数，则说明网中存在环，不能求关键路径，算法终止；否则执行步骤3；
3.从汇点vn-1出发，令vl[n-1]=ve[n-1]，按逆拓扑有序求其余各顶点事件的最迟发生时间vl[i](2≤i≤n-2)；
4.根据各顶点的ve、vl值，求每条弧s的最早开始时间e(s)和最迟开始时间l(s)，若某条弧满足条件e(s)=l(s)，则为关键活动。

1.自己定义栈

package com.cn.graph;

import java.util.Arrays;

class Stack {
	private Object[] elementData;
	private int currentCapacity;
	private int base;
	private int top;
	private int capacityIncrements;
	private int initCapacity;
	
	public Stack(){
		base = 0;
		top = 0;
		initCapacity = 10;
		capacityIncrements = 10;
		currentCapacity = initCapacity;
		elementData = new Object[initCapacity];
	}
	
	public void push(Object obj) {
		if (top < currentCapacity) {
			elementData[top++] = obj;
		}
		else {
			//扩容
			currentCapacity += capacityIncrements; 
			ensureCapacityHelper();
			elementData[top++] = obj;
		}
	}

	private void ensureCapacityHelper() {
		elementData = Arrays.copyOf(elementData, currentCapacity);
	}
	public int getSize() {
		return top;
	}
	
	public Object pop() throws Exception {
		if (top > base) {
			Object obj = elementData[top - 1];
			elementData[top--] = null;
			return obj;
		} else {
			throw new ArrayIndexOutOfBoundsException("stack is null");
		}
	}
	
	
	public String toString() {
		String str = "";
		for (int i = 0; i < top; i ++) {
			str += elementData[i].toString() + " ";
		}
		return str;
	}
	
	
	public Object getTop() {
		return elementData[top - 1];
	}
	
	public boolean isEmpty() {
		if (base == top) {
			return true;
		} else {
			return false;
		}
		
	}
	
	
	
}

2.自定义一个异常

package com.cn.tree;

public class MyException extends Exception {
	private static final long serialVersionUID = 1L;
	public MyException(String str) {
		super(str);
	}
	public MyException() {}
}

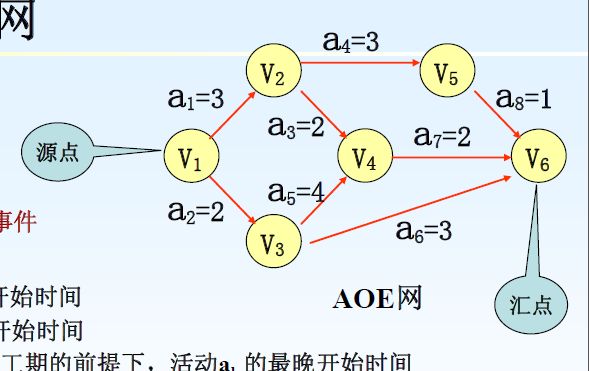
3.AOE网

4.定义邻接表数据结构

/**
 * 表结点结构
 * @author Administrator
 *
 */
class ArcNode {
	int adjvex;//表头顶点的邻接顶点编号
	int data;//边的信息
	int edge;
	ArcNode nextArc;//指向下一个邻接顶点的指针
	
	public ArcNode(int adjvex, int data, int edge, ArcNode nextArc) {
		this.adjvex = adjvex;
		this.data = data;
		this.nextArc = nextArc;
		this.edge = edge;
	}

	public int getAdjvex() {
		return adjvex;
	}

	public void setAdjvex(int adjvex) {
		this.adjvex = adjvex;
	}

	public int getData() {
		return data;
	}

	public void setData(int data) {
		this.data = data;
	}

	public ArcNode getNextArc() {
		return nextArc;
	}

	public void setNextArc(ArcNode nextArc) {
		this.nextArc = nextArc;
	}
}

/**
 * 头结点结构
 * @author Administrator
 *
 */
class HeadNode {
	String data;//节点的信息
	ArcNode firstArc;//指向第一个邻接顶点的指针
	public HeadNode() {

	}
	public HeadNode(String data) {
		this.data = data;
	}
	public HeadNode(String data, ArcNode firstArc) {
		this.data = data;
		this.firstArc = firstArc;
	}
	public String getData() {
		return data;
	}
	public void setData(String data) {
		this.data = data;
	}
	public ArcNode getFirstArc() {
		return firstArc;
	}
	public void setFirstArc(ArcNode firstArc) {
		this.firstArc = firstArc;
	}
}

5.求关键路径

package com.cn.graph;

import com.cn.tree.MyException;
public class AdjacencyList {
	public static void main(String[] args) throws Exception {
		//v1
		ArcNode an1 = new ArcNode(3, 2, 2, null);
		ArcNode an2 = new ArcNode(2, 3, 1,an1);
		
		//v2
		ArcNode an3 = new ArcNode(5, 3, 4, null);
		ArcNode an4 = new ArcNode(4, 2, 3, an3);
		
		//v3
		ArcNode an5 = new ArcNode(4, 4, 5, null);
		ArcNode an6 = new ArcNode(6, 3, 6, an5);
		
		//v4
		ArcNode an7 = new ArcNode(6, 2, 7, null);
		
		//v5
		ArcNode an8 = new ArcNode(6, 1, 8, null);
		
		//定义一个图
		HeadNode n1 = new HeadNode("v1", an2);
		HeadNode n2 = new HeadNode("v2", an4);
		HeadNode n3 = new HeadNode("v3", an6);
		HeadNode n4 = new HeadNode("v4", an7);
		HeadNode n5 = new HeadNode("v5", an8);
		HeadNode n6 = new HeadNode("v6", null);
		
		HeadNode[] hns = new HeadNode[]{n1, n2, n3, n4, n5, n6};
		
		/*//test
		ArcNode an = hns[0].firstArc;
		int i = an.adjvex;
		int j = an.nextArc.adjvex;
		
		HeadNode h = hns[i - 1];
		HeadNode h2 = hns[j - 1];
		
		System.out.println(h.getData());
		System.out.println(h2.getData());*/
		
		//球关键路径
		Stack s = new Stack();
		Stack t = new Stack();
		int[] inDegree = new int[hns.length];
		for (int i = 0; i < inDegree.length; i++) {
			inDegree[i] = 0;
		}
		/**
		 * 1.事件vj的最早发生时间ve[j]
		 * ve[1]=0
		 * ve[j]=Max{ve(i)+dut() }
		 * ve[j]等于从源点到顶点vj的最长路径的长度
		 */
		int[] ve = new int[hns.length];
		for (int i = 0; i < ve.length; i++) {
			ve[i] = 0;
		}
		
		toplogicalOrder(hns, s, inDegree, t, ve);
		System.out.println("-----------每个点的度数");
		for (int i = 0; i < inDegree.length; i++) {
			System.out.println(inDegree[i]);
		}
		System.out.println("-----------事件的最早发生时间");
		for (int i = 0; i < ve.length; i++) {
			System.out.println(ve[i]);
		}
		
		/**
		 * 2.事件vi的最晚发生时间vl[i]
		 * vl[n]=ve[n]
		 * vl[i]=Min{vl(j)-dut()}
		 */
		int[] vl = new int[hns.length];
		for (int i = 0; i < vl.length; i++) {
			vl[i] = ve[ve.length - 1];
		}
		
		lastHappen(hns, vl, t);
		System.out.println("-----------时间的最晚发生时间");
		for (int i = 0; i < vl.length; i++) {
			System.out.println(vl[i]);
		}
		
		/**
		 * 3.活动ak的最早开始时间e[k]
 		 * e[k]=ve[i]
		 */
		//8 是边的数目
		int[] e = new int[8];
		for (int i = 0; i < e.length; i++) {
			e[i] = 0;
		}
		activityEarly(hns, e, ve);
		System.out.println("-------------活动的最早开始时间");
		for (int i = 0; i < e.length; i++) {
			System.out.println(e[i]);
		}
		
		/**
		 * 4.活动ak的最晚开始时间l[k]
		 * l[k]=vl[j] -dut()
		 */
		
		int[] l = new int[8];
		for (int i = 0; i < l.length; i++) {
			l[i] = 0;
		}
		activityLast(hns, l, vl);
		System.out.println("------------活动的最晚开始时间");
		for (int i = 0; i < l.length; i++) {
			System.out.println(l[i]);
		}
	
		/**
		 * 若某条弧满足条件e(s)=l(s)，则为关键活动。
		 */
		System.out.println("------------关键路径");
		Stack key = new Stack();
		keyWay(key, e, l);
		//下面打印出关键活动
		System.out.println(key);
		
		
		
	}

	private static void keyWay(Stack key, int[] e, int[] l) {
		for (int i = 0; i < e.length; i++) {
			if (e[i] == l[i]) {
				key.push(i + 1);
			}
		}
		
	}

	private static void activityLast(HeadNode[] hns, int[] l, int[] vl) {
		for (int i = 0; i < hns.length; i++) {
			for (ArcNode n = hns[i].firstArc; n != null; n = n.nextArc) {
				int k = n.adjvex - 1;
				int j = n.edge;
				l[j - 1] = vl[k] - n.data;
			} 
			
		}
		
		
	}

	private static void activityEarly(HeadNode[] hns, int[] e, int[] ve) {
		for (int i = 0; i < hns.length; i++) {
			for (ArcNode n = hns[i].firstArc; n != null; n = n.nextArc) {
				int j = n.edge;
				e[j - 1] = ve[i];
			}
			
		}
		
	}

	private static void lastHappen(HeadNode[] hns, int[] vl, Stack t) throws Exception {
		int i = (Integer) t.pop();
		while (!t.isEmpty()) {
			i = (Integer) t.pop();
			for (ArcNode n = hns[i].firstArc; n != null; n = n.nextArc) {
				int j = n.adjvex - 1;
				if (vl[i] > vl[j] - n.data) {
					vl[i] = vl[j] - n.data;
				}
			}
		}
	}

	private static void toplogicalOrder(HeadNode[] hns, Stack s, int[] inDegree, Stack t, int[] ve) throws Exception {
		//求每个节点的入度
		for (int i = 0; i < hns.length; i++) {
			for (ArcNode n = hns[i].firstArc; n != null; n = n.nextArc) {
				inDegree[n.adjvex - 1] ++;
			}
		}
		//入度为0的顶点保存在栈中
		for (int i = 0; i < inDegree.length; i++) {
			if (inDegree[i] == 0) {
				s.push(i);
			}
		}
		
		int count = 0;
		
		while (!s.isEmpty()) {
			int i = (Integer) s.pop();
			t.push(i);
			count++;
			for (ArcNode n = hns[i].firstArc;n != null; n = n.nextArc) {
				int j = n.adjvex - 1;
				inDegree[j]--;
				if (inDegree[j] == 0) {
					s.push(j);
				}
				if (ve[i] + n.data > ve[j]) {
					ve[j] = ve[i] + n.data;
				}
			}
		}
		if (count < hns.length) {
			throw new MyException("有环！");
		}
		
		
	}
}