糖尿病的治疗效果分析

1．       数据介绍

1.1 数据来源

数据来自442名糖尿病患者，分别测量了他们的10个基线变量（年龄，性别，身体质量指数，平均血压，六个血清测量值和感兴趣的、基于一年观察期之后得到的一个数量度量指标，即一个疾病的进展指标）。要求建立一个模型，通过10个自变量年龄、性别、BMI、BP、TC、LDL、HDL、TCH、LTG和GLU来预测响应变量Y。

 

1.2 数据背景

糖尿病是一组由于胰岛素分泌缺陷和胰岛素作用障碍所致的以高血糖为特征的代谢性疾病。

要有效地治疗糖尿病，必须要先明确糖尿病的治疗目标，从而选择正确的治疗方法，达到理想的治疗效果。糖尿病治疗的目标主要有以下几个方面：(1)纠正高血糖和高血脂等代谢紊乱，促使糖、蛋白质和脂肪的正常代谢。(2)缓解高血糖等代谢紊乱所引起的症状。 (3)防治酮酸症中毒等急性并发症和防治心血管、肾脏、眼睛及神经系统等慢性病变，延长患者寿命，降低病死率。(4)肥胖者应积极减肥，维持正常体重，保证儿童和青少年的正常生长发育，保证糖尿病孕妇和妊娠期糖尿病产妇的顺利分娩，维持成年人正常劳动力，提高老年糖尿病患者的生存质量。

 

1.3数据分析

从数据信息可知Y越小说明糖尿病的治疗效果越好，我们将Y称为糖尿病指数。根据文献[1]，对于胰岛素治疗糖尿病的效果表明，性别和年龄对治疗效果无显著影响，故我们认为这两个变量可去掉。而TC和TCH这两个变量都有明显下降，所以我们认为这且其与糖尿病指数可能是成正相关的。据国外最新研究结果显示，对于肥胖的儿童患者，体重越重、身材越肥胖，其糖尿病血糖控制情况越差。于是，认为BMI指数对治疗效果可能有影响的，与糖尿病指数也可能是正相关的。理论上，糖尿病人的血压应当控制在病人能够耐受的尽可能较低的血压水平。从这个角度讲，血压（BP）与糖尿病指数可能正相关。众所周知，低密度脂蛋白胆固醇增高以及高密度脂蛋白胆固醇降低是引起粥样硬化的主要“元凶”。在临床治疗中，对于血脂紊乱我们主要采取调脂的治疗方法，即努力提高高密度脂蛋白水平，同时努力降低低密度脂蛋白水平，所以LDL可能与糖尿病指数正相关，而HDL可能与糖尿病指数负相关。这与计算Y与各解释变量的相关系数的结果是一致的。

 

 

2．  建模过程

 

2.1 变量选择（最小角回归）

最小角回归（Leastangle regression ），Efron于2004年提出的一种变量选择的方法，类似于向前逐步回归(ForwardStepwise)的形式。LAR是每次先找出和因变量相关度最高的那个变量, 再沿着LSE的方向一点点调整这个predictor的系数，在这个过程中，这个变量和残差的相关系数会逐渐减小，等到这个相关性没那么显著的时候，就要选进新的相关性最高的变量，然后重新沿着LSE的方向进行变动。而到最后，所有变量都被选中，就和LSE相同了。注意：用LAR时的Y都已经中心化，X中心标准化过了。

先对变量赋一个名称，将年龄age赋值x1,性别sex赋值x2,BMI指数赋值x3,BP平均血压赋值x4,TC血清总胆固醇赋值x5,LDL低密度脂蛋白赋值x6,HDL高密度脂蛋白赋值x7,TCH总循环血红蛋白量赋值x8,LTG赋值x9,GLU葡萄糖浓度赋值x10,进度指标为Y。计算y与解释变量x的相关系数得：

          y

x1   0.1878888

x2   0.0430620

x3   0.5864501

x4   0.4414818

x5   0.2120225

x6   0.1740536

x7  -0.3947893

x8   0.4304529

x9   0.5658826

x10  0.3824835

对x进行中心标准化，对y进行中心化后用LAR进行变量选择，得到结果：

LASSO sequence

Computing X'X .....

LARS Step 1 :    Variable 3     added

LARS Step 2 :    Variable 9     added

LARS Step 3 :    Variable 4     added

LARS Step 4 :    Variable 7     added

LARS Step 5 :    Variable 2     added

LARS Step 6 :    Variable 10    added

LARS Step 7 :    Variable 5     added

LARS Step 8 :    Variable 8     added

LARS Step 9 :    Variable 6     added

LARS Step 10 :   Variable 1     added

Lasso Step 11 :  Variable 7    dropped

LARS Step 12 :   Variable 7     added

Computing residuals, RSS etc.....

从LAR的结果知，解释变量与y的相关度由高到低为x3,x9,x4,x7,

x10,x5,x8,x6.

 

2.2 建立线性模型

根据LAR对变量的选择结果，先对y与前面五个变量做线性回归，得到如下结果：

Call:

lm(formula = y ~ x3 +x9 + x4 + x7 + x10)

 

Residuals:

     Min      1Q   Median       3Q     Max

-140.572  -40.434  -2.097   39.183  151.750

 

Coefficients:

             Estimate Std. Error t valuePr(>|t|)   

(Intercept)-267.5988    35.8936  -7.455 4.87e-13 ***

x3             5.9384     0.7186  8.263 1.72e-15 ***

x9            43.4757     6.3264  6.872 2.20e-11 ***

x4             0.9090     0.2199  4.134 4.27e-05 ***

x7            -0.7074     0.2287 -3.093  0.00211 **

x10            0.1151     0.2721  0.423  0.67258   

---

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’1

 

Residual standarderror: 55.28 on 436 degrees of freedom

Multiple R-squared:0.4917,    Adjusted R-squared: 0.4859

F-statistic: 84.35 on 5and 436 DF,  p-value: < 2.2e-16

    看这五个变量有无多重共线性，即计算方差膨胀因子，得：

      x3       x9       x4       x7      x10 

1.454913 1.576340 1.334533 1.263197 1.412587 

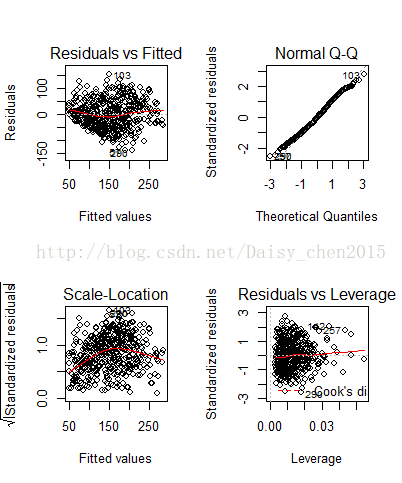
由于方差膨胀因子大于10时认为是存在多重共线性，所以这五个变量之间不存在共线性。画出一些图来看这个模型的拟合效果。

 

                        图1 线性模型的拟合效果

 

从图1可以看出，残差基本上在零附近，而QQ图也显示大部分点都集中在直线上，说明拟合效果挺好的。而从上面的回归结果可以看出这5个解释变量的符号与分析的一致，且只有x10的系数在5%的显著性水平下是不显著的。另外，尝试将剩下的其它三个变量加入模型中发现，若将x5(或x6)加入模型中，得到系数符号与分析不符且不显著，更重要的是残差平方和比上面的模型大；而将x8加入模型时，估计的系数不显著，而且符号也不符合，残差平方和也只是变小了一点点，于是认为这是最佳的线性模型。 

  

2.3 建立非参数模型

下面再看非参数模型：

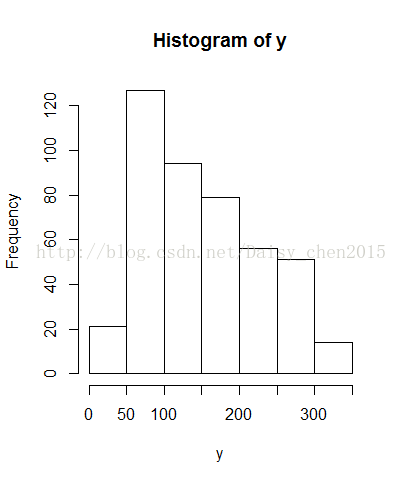
首先画y的直方图：

对数据做广义线性模型，从y的直方图可以看出，family可选Gamma函数,得到结果如下：

Call:

glm(formula = y ~ x3 + x4 + x5 + x6 + x7 + x8 + x9 + x10, family = Gamma)

Deviance Residuals: 

     Min        1Q    Median        3Q       Max  

-1.26945  -0.33060  -0.05384   0.24495   0.98677  

Coefficients:

              Estimate Std. Error t value Pr(>|t|)    

(Intercept)  3.340e-02  3.692e-03   9.046  < 2e-16 ***

x3          -1.812e-04  2.807e-05  -6.454 2.93e-10 ***

x4          -3.566e-05  9.243e-06  -3.857 0.000132 ***

x5           9.636e-05  2.649e-05   3.638 0.000308 ***

x6          -9.685e-05  2.409e-05  -4.021 6.83e-05 ***

x7          -4.266e-05  3.972e-05  -1.074 0.283421    

x8           1.979e-04  2.631e-04   0.752 0.452485    

x9          -4.955e-03  8.324e-04  -5.953 5.44e-09 ***

x10         -6.160e-06  1.163e-05  -0.530 0.596526    

---

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

(Dispersion parameter for Gamma family taken to be 0.1549709)

    Null deviance: 126.797  on 441  degrees of freedom

Residual deviance:  70.869  on 433  degrees of freedom

AIC: 4792.2

Number of Fisher Scoring iterations: 5

 

画出一些图来看拟合的效果：

              图2 非参数模型的拟合效果

 

由于结果中x7,x8,x10的系数都不显著，我们尝试去掉变量x8，得到结果:

Call:

glm(formula = y ~ x3 + x4 + x5 + x6 + x7 + x9 + x10, family = Gamma)

Deviance Residuals: 

     Min        1Q    Median        3Q       Max  

-1.26768  -0.32988  -0.05082   0.24679   0.99412  

Coefficients:

              Estimate Std. Error t value Pr(>|t|)    

(Intercept)  3.470e-02  3.262e-03  10.637  < 2e-16 ***

x3          -1.809e-04  2.800e-05  -6.462 2.78e-10 ***

x4          -3.626e-05  9.198e-06  -3.942 9.41e-05 ***

x5           1.043e-04  2.426e-05   4.299 2.12e-05 ***

x6          -1.002e-04  2.360e-05  -4.245 2.68e-05 ***

x7          -6.434e-05  2.728e-05  -2.358   0.0188 *  

x9          -5.064e-03  8.182e-04  -6.190 1.40e-09 ***

x10         -5.914e-06  1.163e-05  -0.508   0.6115    

---

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

(Dispersion parameter for Gamma family taken to be 0.1549408)

    Null deviance: 126.797  on 441  degrees of freedom

Residual deviance:  70.958  on 434  degrees of freedom

AIC: 4790.7

Number of Fisher Scoring iterations: 5

再看一些这个模型的拟合效果：

去掉变量x8之后残差平方和相差很小，AIC也更小了,Null deviance不变，Residual deviance变化也很小，于是从模型中去掉x8.

 

 

2.4 建立部分线性模型

接下来我们尝试用部分线性的模型去拟合，将葡萄糖浓度x10作为非线性的部分，结果如下：

Call: gam(formula = y ~ x3 + x4 + x5 + x6 + x7 + x9 + s(x10), family = Gamma)

Deviance Residuals:

     Min       1Q   Median       3Q      Max 

-1.26530 -0.33472 -0.05991  0.23848  0.98470 

(Dispersion Parameter for Gamma family taken to be 0.155)

    Null Deviance: 126.7969 on 441 degrees of freedom

Residual Deviance: 70.3203 on 430.9992 degrees of freedom

AIC: 4792.637 

Number of Local Scoring Iterations: 6 

DF for Terms and F-values for Nonparametric Effects

            Df Npar Df Npar F  Pr(F)

(Intercept)  1                      

x3           1                      

x4           1                      

x5           1                      

x6           1                      

x7           1                      

x9           1                      

s(x10)       1       3 1.3827 0.2475

 

接下来检验拟合的模型的系数的显著性：

 

z test of coefficients:

               Estimate  Std. Error z value  Pr(>|z|)    

(Intercept)  3.5256e-02  3.2510e-03 10.8447 < 2.2e-16 ***

x3          -1.8286e-04  2.8131e-05 -6.5003 8.018e-11 ***

x4          -3.6551e-05  9.2145e-06 -3.9666 7.290e-05 ***

x5           1.0866e-04  2.4245e-05  4.4818 7.403e-06 ***

x6          -1.0466e-04  2.3600e-05 -4.4348 9.217e-06 ***

x7          -6.8329e-05  2.7273e-05 -2.5054   0.01223 *  

x9          -5.2069e-03  8.1793e-04 -6.3660 1.940e-10 ***

s(x10)      -4.9875e-06  1.1381e-05 -0.4382   0.66121    

---

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

除了作为非线性部分的x10的系数不显著之外，其它的都显著，但是系数的符号与分析的不符合。而且此时通过  Null deviance 与Residual deviance的减小，我们可以判断出将葡萄糖浓度放入非线性部分还是可行的。但是从图中可看出所有的变量都是不显著的。

分别计算三个模型的残差平方和：

第一个线性模型的残差平方和： 2.199218e-25；

第二个非参数模型的残差平方和：2.961572e-17；

第三个部分线性模型的残差平方和：4.244529e-13；

 

从拟合的残差平方和来看，第一个线性模型最优。

 

3.结论

综合上面分析，对于该数据，拟合的最优模型为第一个线性模型：

.

也就是说LTG这一个量对糖尿病指数的影响最大，依次是BMI指数，平均血压（BP），高密度脂蛋白（HDL）和葡萄糖浓度（GLU）。

 

4.参考文献

[1].龙伟东.2型糖尿病短期胰岛素强化治疗效果的影响因素分析[期刊论文]中国临床实用医学.2010,04（2）.

[2].BRADLEY EFRON, TREVOR HASTIE, IAIN JOHNSTONE AND ROBERT TIBSHIRANI .LEAST  ANGLE REGRESSION. The Annals ofStatistics2004, Vol. 32, No. 2, 407–499.