逆波兰式实现四则运算表达式计算器支持括号、十六进制

   最近做一个题目，要求实现简单的四则运算、支持括号和十六进制、浮点数等。同时能够进行输入合法检查。

      用逆波兰式（后缀表达式）实现时主要包括以下几个主要部分：

              栈操作：包括入栈、出栈、是否为空、栈顶元素等，由于在栈操作中需要char型和float型，需要创建模板。

              输入合法检查：包括输入合法字符、输入括号匹配、输入括号匹配、输入正确的十六进制、运算符无或连续。

              提取输入表达式：由于输入的表达式中有浮点数或者十六进制数需要提取出来。

              中缀表达式转化为后缀表达式：输入的表达式为中缀表达如a+b*c+(d*e+f)*g,需要将该表达式转化为后缀表达式即abc*+de*f+g*+。

               计算后缀表达式：从而得到计算结果

               计算结果输出处理：包括判断是否为有十六进制，对含有十六进制表达式的输出结果需要分析是否需要输出十六进制、输出结果是否为整数等

分别分析如下：

        由于输入的表达式中有数字、字符等，在后来的栈操作时需要的不仅是char型的，还需要float型（int型数字也可以用float处理）。所以栈操作如下：定义栈模板。并实现具体操作：

//自定义一个栈模板
template 
class stack
{
public:
	stack(){top = -1;}
	T topElem();
	T pop();
	bool isEmpty();
	void push(T _elem);
private:
	T elem[g_iconstArrayMax];
	int top;
};

//入栈
template 
void stack::push(T _elem)
{
	if (top == g_iconstArrayMax - 1)
	{
		printf("栈满!\n");
	}
	else
	{
		top++;
		elem[top] = _elem;
	}
}

//出栈
template 
T stack::pop()
{
	if (top == -1)
	{
		printf("栈空!\n");
		return 0;
	}
	else
	{
 		T x = elem[top--];
 		return x;
	}
}

//返回栈顶元素
template 
T stack::topElem()
{
	if (top == -1)
	{
		printf("栈空!\n");
		return 0;
	}
	else
	{
		return elem[top];
	}
}

//是否为空
template 
bool stack::isEmpty()
{
	if (top == -1)
	{
		return true;
	}
	else
	{
		return false;
	}
}

在对输入的表达式进行分析，由于输入的表达式中有可能哟float、十六进制，整数，于是需要对输入的表达式进行分析，将操作数和操作符分别提取出来。并在提取的同时将char型型计算出float int和十六进制数字，并将十六进制数字转化为int方便后来的计算。

该功能由函数实现如下，在该函数中分别将数字存储在figure中，并将操作数用figure中的下标+1代替，结合操作符将，原表达式如1.23+0x23*2+（1.5*3-0.5）*2转化为仅包含int型下标和操作符如1+2*3+（4*5-6）*7的存储于dest中：

//把数字都拆出来，然后放进figure数组中，将原字符串复制到dest中，
//同时，数字全部用figure中对应的小标代替
void cToFig(char* dest,char* str,float* figure)
{
	if (NULL == str)
	{
		printf("字符串为空！\n");
	}
	else
	{
		int j = 0;
		int figNum= 0;//figure下标
		int powNum = 1;//pow的次数
		int destNum = 0;//dest的下标
		int i = 0;

		while(str[i]!='\0')
		{
			if (str[i] >= '0' && str[i] <= '9')
			{
				j = i+1;
				int inte = 0;//整数
				float fnum = 0.0;//浮点数

				if (str[j] == 'x')//出现十六进制
				{
					j++;
					while ((str[j]!= NULL)&&(!isOperator(str[j])))
					{
						j++;
					}
					//计算出十六进制
					for (int k = i+2; k < j; k++)
					{
						if (str[k] >= '0' && str[k] <= '9')
						{
							inte = inte*16+(str[k]-'0');//这里要区分是不是0-9 a-f
						}
						else
						{
							inte = inte*16+(str[k]-87);
						}	
					}
					figure[figNum] = inte;
					dest[destNum] = figNum + '1';
					destNum++;
					figNum++;
					i= j;
				}
				else
				{
					while(str[j]>='0' && str[j] <= '9')
					{
						j++;
					}
					j--;

					for (int k = i; k <= j; k++)
					{
						inte = inte*10+str[k]-'0';
					}
					j++;

					if (str[j] == '.')
					{
						powNum = 1;
						i = j+1;
						j = j+1;
						while(str[j]>='0' && str[j] <= '9')
						{
							j++;
						}
						for (int k = i; k < j; k++)
						{
							float tempf = pow(0.1,powNum);
							powNum++;
							fnum=fnum+tempf*(str[k]-'0');
						}
						i = j;
						figure[figNum] = inte+fnum;
						dest[destNum] = figNum + '1';
						destNum++;
						figNum++;
					}
					else
					{
						i = j;
						figure[figNum] = inte;
						dest[destNum] = figNum + '1';
						destNum++;
						figNum++;
					}
				}
			}
			else 
			{
				dest[destNum] = str[i];
				i++;
				destNum++;
			}
		}
		dest[destNum] = '\0';
	}
}

然后是将转化后的仅包含int型的中缀表达式转化为后缀表达式。中缀表达式转化为后缀表达式需要借助栈，当遇到操作数时放入数组压入栈，当遇到操作符时与栈顶元素进行比较，如果优先级低于栈顶元素则依次弹出，否则入栈，当遇到‘（’，直接压栈，但是遇到‘）'，将栈内元素依次弹入到数组中直到遇到‘（’，具体实现如下：

void midToback(char* backStr, char* midStr,int& m)
{
	if (NULL == midStr)
	{
		printf("表达式为空！\n");
	}
	else
	{
		stack oper;
		//initStack(oper);
		int len = strlen(midStr);

		//char operOfMid = '\0';

		for (int i = 0; i < len; i++)
		{
			//遇见表示操作数的数组下标
			if (midStr[i] >= '1')
			{
				backStr[m] = midStr[i];
				m++;
			}
			else if (midStr[i] == '(')
			{
				oper.push(midStr[i]);
			}
			else if (midStr[i] == '+')
			{
				//operOfMid = oper.top();
				while (!oper.isEmpty()&&((oper.topElem()=='-') ||(oper.topElem()=='*')||(oper.topElem()=='/')||(oper.topElem()=='+')))
				{
					backStr[m++] = oper.topElem();
					oper.pop();
				}
				oper.push(midStr[i]);
			}
			else if (midStr[i] == '-')
			{
				while (!oper.isEmpty()&&((oper.topElem()=='-') ||(oper.topElem()=='*')||(oper.topElem()=='/')))
				{
					backStr[m++] = oper.topElem();
					oper.pop();
				}
				oper.push(midStr[i]);
			}
			else if ((midStr[i] == '*')||(midStr[i] == '/'))
			{
				oper.push(midStr[i]);
			}
			else if (midStr[i] == ')')
			{
				while(oper.topElem()!= '(')
				{
					backStr[m++] = oper.topElem();
					oper.pop();
				}
				oper.pop();
			}
		}
		while(!oper.isEmpty())
		{
			backStr[m++] = oper.topElem();
			oper.pop();
		}
		backStr[m] = '\0';
	}
}

在得到后缀表达式后，对表达式进行计算，如后缀表达式为123*+45*6-7*+，同样借助栈操作，当遇到操作数时压入栈，遇到操作符则依次弹出两个栈顶元素计算（需要注意：一、计算顺序，二、压入的是下标，计算时需要将对应的操作数提取出来计算）后压入栈，实现如下：

float calcu(char* backStr,int m, float* fig)
{
	stack sResult;//定义float栈放计算结果

	float a,b,c,result = 0.0;

	for (int i = 0; i< m;i++)
	{
		if (backStr[i]>='1')
		{
			//将数字对应到float中的数字，并放入栈
			int tempSubscript = backStr[i]-'1';
			sResult.push(fig[tempSubscript]);
		}
		else if(backStr[i] == '-')
		{
			a = sResult.pop();
			b = sResult.pop();
			c = b-a;
			sResult.push(c);
		}
		else if (backStr[i] == '+')
		{
			a = sResult.pop();
			b = sResult.pop();
			c = b+a;
			sResult.push(c);
		}
		else if (backStr[i] == '*')
		{
			a = sResult.pop();
			b = sResult.pop();
			c = b*a;
			sResult.push(c);
		}
		else if (backStr[i] == '/')
		{
			a = sResult.pop();
			b = sResult.pop();
			c = b/a;
			sResult.push(c);
		}
	}
	result = sResult.pop();
	return result;
}

计算结果出来之后，需要对计算结果进行分析：首先表达式中是否有十六进制，如果有十六进制且结果为整数则需要转化为十六进制输出，否则就按照i整数或者小数输出，所以这里还需要进行判断是否为整数，和十进制转化为十六进制。

void tenToSixteen(char* sixteen,int n)
{
	int shang = 0;
	int yushu = 0;
	int value = 1;
	int i = 0;
	while(value <= n)
	{
		value = value*16;
		yushu = n % value;
		shang = yushu * 16 /value;

		if (shang >=0 && shang <=9)
		{
			sixteen[i] = (char)(shang+48);
		}
		else
		{
			sixteen[i] =(char)(shang+87);
		}
		i++;
	}
	char str[g_iconstArrayMax] = "0x";
	strrev(sixteen);
	strcat(str,sixteen);
	strcpy(sixteen,str);
}

//判断结果是不是int型
bool isInte(float fresult)
{
	char fresultStr[g_iconstArrayMax];

	sprintf(fresultStr,"%f",fresult);
	
	if (NULL == fresultStr)
	{
		return false;
	}
	else
	{
		int len = strlen(fresultStr);
		int i = 0;
		while (fresultStr[i]!='.')
		{
			i++;
		}

		if (fresultStr[i+1] == '0')
		{
			return true;
		}
		else
		{
			return false;
		}
	}
}

另外关于输入是否合法的检查，两个函数实现一个进行具体的判断，另一个判断括号是否匹配，同样利用栈操作实现：

bool IsMatch(char* str)
{
	//初始化栈
	stack s;
	//initStack(s);

	int len = strlen(str);

	char pp[g_iconstArrayMax];
	char temp;
	int k = 0;

	for (int i= 0; i '9')
			{
				if ((str[i] < 'a'))
				{
					printf("输入非法字符！\n");
					return false;
				}
				else if ((str[i] > 'f')&&(str[i] != 'x'))
				{
					printf("输入非法字符！\n");
					return false;
				}
				else if(str[i] == 'x')
				{
					if (str[i-1] != '0')
					{
						printf("输入十六进制非法，请以0x开头！\n");
						return false;
					}
				}
				else
				{
					if (str[i-1]!='x')
					{
						printf("输入非法字符！\n");
						return false;
					}	
				}
			}
		}
		//检测括号匹配
		if (!IsMatch(str))
		{
			printf("括号不匹配！\n");
			return false;
		}
		//检测是否出现连续的运算符或者没有运算法
		int num = 0;
		int k = 0;
		for (int j = 0; j< len; j++)
		{
			if ((str[j] == '+')||(str[j] == '-')||(str[j] == '*')
				||(str[j] == '/'))
			{
				num++;
				k = j;
				if ((str[k-1] == '+')||(str[k-1] == '-')||(str[k-1] == '*')
					||(str[k-1] == '/')||(str[k+1] == '+')||(str[k+1] == '-')||(str[k+1] == '*')
					||(str[k+1] == '/'))
				{
					printf("出现连续运算符！\n");
					return false;
				}
				else if ((str[j] == '/')&&(str[k+1] == '0'))
				{
					printf("被除数不能为0！\n");
					return false;
				}
				else if (str[k+1] == NULL)
				{
					printf("输入不完整！\n");
					return false;
				}
			}
		}

		if (num == 0)
		{
			printf("无运算符！\n");
			return false;
		}
		return true;
	}
}

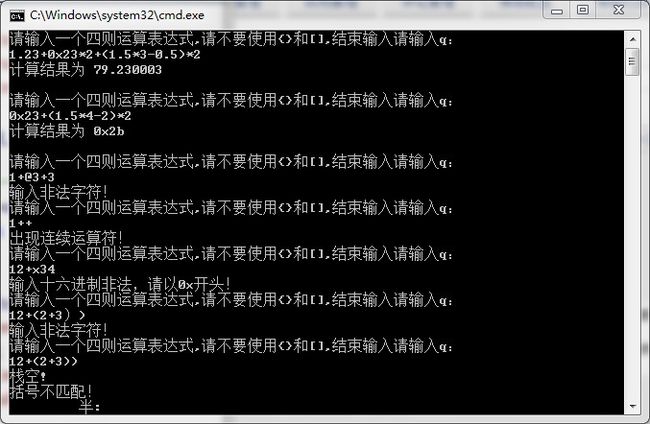
实现结果如下：