数据流分析（三）

想学数据流分析的人还是找一个国外大学的讲义学吧，以下内容都是自己多年前按照自己的理解写的，很多内容可能会误人子弟，sorry

---

#引子
在数据流分析（一）和数据流分析（二）中我们介绍了数据流分析的基本模式以及到达定值和活变量的分析。在这篇文章中我们简要介绍一下可用表达式和数据流分析中的格。

• 可用表达式
• 数据流分析中的格

---

##可用表达式

如果从流图入口结点到达程序点 p 的每条路径都对表达式 x + y 求值，且从最后一个这样的求值之后到p点的路径上没有再次对x或y赋值，那么 x + y 在 p 点上可用(available)。

注意在可用表达式的定义中，我特意加黑了每条路径，这是和到达定值不同的，对于到达定值来说至少存在一条这样的路径即可。

对于可用表达式数据流模式而言，如果一个基本块对 x 或 y 赋值（或可能对它们赋值），并且之后没有再重新计算 x + y，我们就说该基本块“杀死”了表达式 x + y。

如果一个基本块一定对 x + y 求值，并且之后没有再对 x 或 y 定值，那么这个基本块生成表达式 x + y 。

可用表达式信息的主要用途就是寻找全局公共子表达式。每个程序都有有限个表达式，这有限个表达式就是可用表达式数据流分析的值域，也就是每个程序点的可用表达式就是这个值域的子集。

int z = x * y;
print s + t;
int w = u / v;
// ...
// program contains expressions { x * y, s + t, u / v, ...}

可用性是表达式在数据流中的一个属性，“这个表达式是否计算过？”。在一条指令之前，每个表达式只能是可用或者不可用，所以通常都是从指令的角度来考虑表达式的可用性，每条指令（或者流图中的一个结点）都关联着一组可用表达式。

int z = x * y;
print s + t;
int w = u / v; // 3: avail(3) = { x * y, s + t}

例如在结点3处，有两条可用表达式**“x * y”** 和 “s + t”。从很多方面来看，可用表达式和活变量都有相似之处，都是数据流的一种属性，并且在每个程序点都关联着一组值的集合。在活跃变量分析中，数据流从后向前传播，一个对 x 的赋值语句，会“杀死”变量x的活跃性，在可用表达式的分析中，数据流从前向后传播，一个对 x 的赋值语句会“杀死”所有包含 x 运算子的表达式。

除了数据流方向这一个区别之外，还有一个很重要的区别，就是在可用表达式分析中，我们必须能够保证该表达式在当前程序点绝对可用，也就是说我们必须保证该表达式被计算过（即使有丢失可用表达式的可能），而不是该表达式在此处可能可用。也就是说可用表达式分析是一种must分析，而活跃变量分析是一种may分析。

如果一个表达式被认为是可用的，我们有可能会做一些比较危险的事情（例如删除重复计算该表达式的指令）。在活变量分析中，更多的活变量就更能够保证安全性，但是在可用表达式中，越少的可用表达式才更能保证安全性。

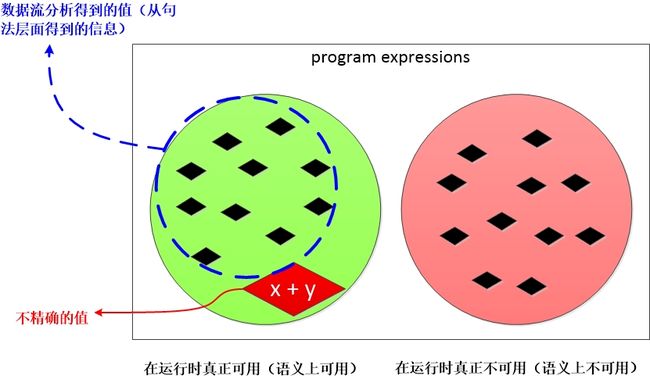
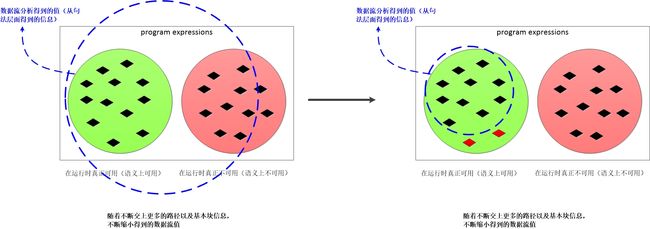
当程序运行时可用表达式和不可用表达式如下图所示，这个图表示的动态执行时的精确解（也就是如果某个基本块不可能执行到，那么这个基本块对可用表达式分析的影响为0）。

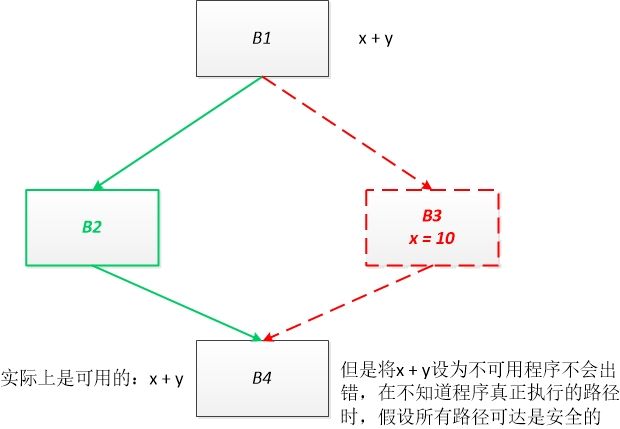
假设有以下代码，在数据流分析中不可能真正确切的知道哪些路径可达，所以假设所有路径可达是安全的，虽然会损失些可以优化的机会。

在安全的前提下，数据流分析还是会尽量向精确靠近，这样才能把优化发挥的更彻底。上述代码对应的可用表达式的图示如下。其中 x + y 是我们在数据流分析的过程中将其杀死的，其实在真正代码的执行过程中，B3块可能不会被真正执行，也就是说 x + y 可能是可用的。但是数据流分析的第一准则是安全性，然后才会在安全的前提下做更为激进的分析。和活变量分析类似，我们尽量会在安全的前提下，向精确解靠近。

我们可以用类似于计算到达定值的方式计算可用表达式。假设 U 是所有出现在程序中一个或多个语句的右部的表达式的全集。对于每个基本块*B***，令IN[ B ]表示在B的开始处可用的的U中的表达式的集合。令OUT[ B ]表示在B的结尾处可用的表达式集合。定义*e_gen[B]***为B生成的表达式的集合，而***e_kill[B]***为被B杀死的U中的表达式的集合。所以我们可以相关的数据流方程和控制流方程。

上面的方程和到达定值的方程组看起来几乎一样，但是一点很重要的区别是这个方程组的交汇运算是交集运算，而不是并集运算。因为只有当一个表达式在一个基本块的多有前驱的结尾处都可用，它才会在该基本块的开头可用。

在到达定值方程的过程中，我们首先假设任何地方都没有定值到达，然后逐渐增大到到达定值的集合，最终构建得到该解。我们最终会求解到达定值方程组，得到符号“到达”定义的最小集合。

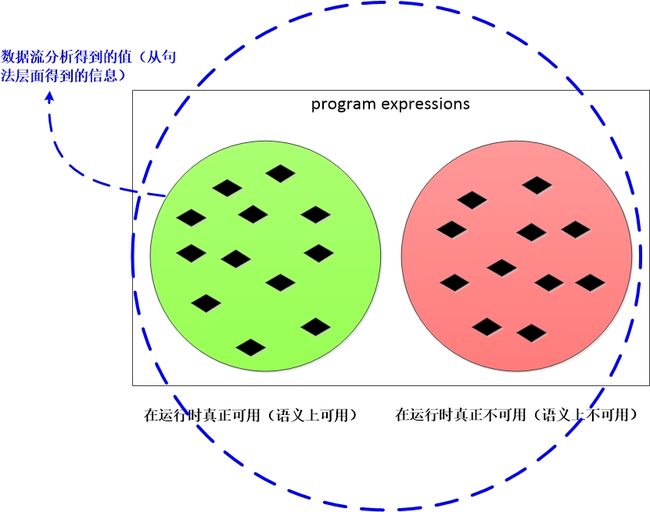
而在求解可用表达式的过程中，我们首先假设除了入口块之外的所有基本块的出口处，所有可用表达式都是可用的，然后不断的将这个解缩小，直到得到一个最大的可用表达式集合的解。

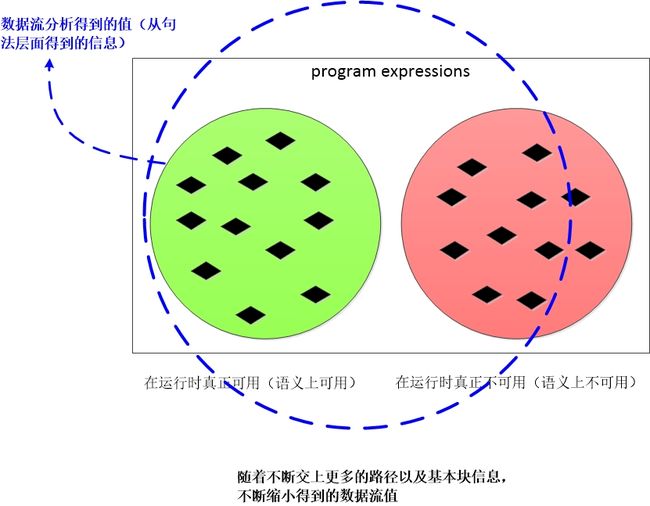
例如我们开始假设所有表达式可用，然后不断的缩减得到的解，直到越过了精确解范畴。

由于数据流分析会忽略所有的路径条件，假设所有的路径可达，所以数据流解的集合会不断的缩小直到一个最大的精确的安全解。

这里我们证明一下为什么考虑全路径的情况下，一定会越过精确解。考虑下面的代码：

（1）多考虑一个路径，肯定会杀死一个原有的可用的表达式
（2）即使多考虑的路径中会生成新的可用表达式，但是由于数据流方程是交集运算，所以单单多考虑的路径的生成还不行，还需要其他的路径都生成该表达式，该表达式才会生成出来。也就是说，多考虑的路径中生成的表达式其实没有任何意义。

例如上图中的代码，假设 B1 -> B3 -> B4 这条路径不可达，B3块会杀死表达式***x + y***，虽然会生成表达式 d + c 但是由于可用表达式的交汇运算时交集，所以必须B2块生成表达式 d + c 才算真正生成表达式 d + c ，也就是无效路径生成的表达式其实没有意思的。也就是多考虑一条路径只会杀死更多的表达式。

不知道一个表达式是可用的只会使我们失去改进代码的机会，而把一个不可用的表达式则会使我们改变程序的计算结果。可用表达式的迭代算法如下所示：

下面我们总结一下前面所提到过的MUST和MAY分析。

特点	May	Must
safe	更大的集合	更小的集合
desired information	small set	large set
Gen	添加可能为真的值	只添加保证为真的值
Kill	只删除保证为假的值	删除所有可能为假的值
merge	union	intersection

通过上面的表格，我们可以看出May分析是尽可能向集合增大的方向前进，而Must分析是尽可能的向集合减小的方向前进。那么有没有一个统一的数据流分析框架来表示呢，不用去关注最终得到的解释最大不动点还是最小不动点，是用交集还是用并集等等。答案是有，后面我们介绍数据流分析中格的概念，格这种数据结构是一个非常直观的表示数据流分析的框架。

---

Sound And Complete

前面我通过可用表达式的例子说明精确解与保守解的概念，其实这种提法并不标准。下面我摘抄《A Brief Introduction to Static Analysis - Sam Blackshear》讲义中的内容。

当我们编写一个程序的时候，我们希望知道程序是否满足某个属性，例如程序P是否没有空指针解引用（NPD），或者程序中的所有的类型转换是否是安全的。如果对程序P进行手工验证，在程序P比较复杂的时候，过程会很繁琐。所以可以通过一个程序（或者静态分析工具）去验证程序P的某些属性是否满足。

但是验证某个程序的属性是不可判定的，见如何理解莱斯定理对程序静态分析的限制。

虽然我们无法得到程序的精确解，但是我们可以使用overapproximation或者underapproximation来尝试得到一个较为精确的解。

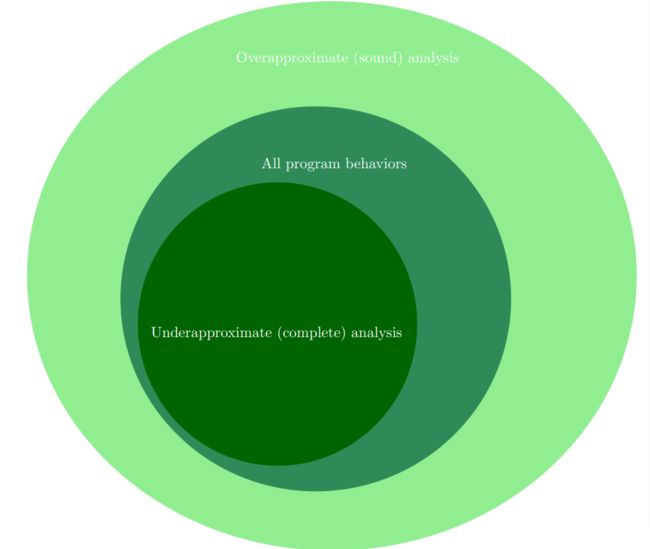
• A sound static analysis overapproximates the behaviors of the program. A sound static analyzer is guaranteed to identify all violations of our property φ, but may also report some “false alarms”, or violations of φ that cannot actully occur.
• A complete static analysis underapproximates the behaviors of the program. Any violation of our property φ reported by a complete static analyzer corresponds to an actual violation of φ, but there is no guarantee that all actual violations of φ will be reported.

上面的的sound static analysis其实就对应我们上面说的保守解，是一种overapproximation，就是考虑程序中实际并不可行的路径，所以能够覆盖完所有的违反属性φ的场景，但是有误报。

而上面的complete static analysis是一种就对应上面我们所描述的超过精确解的值，这些值保证都违反了φ，但是并不能覆盖完所有的值，有漏报。

Note that when a sound static analyzer reports no errors, our program is guaranteed not to violate φ! This is a powerful guarantee. As a result, most static analysis tools choose to be sound rather than complete.

但是在某些静态分析工具中在某些场景中是不可能做到sound的，例如clang static analyzer，在指针场景中，指针ptr有可能指向任意的变量，如果要对指针ptr指向的内存区域进行赋值，"sound static analysis"会将程序中所有变量进行赋值，那么继续向下就会变得非常不精确，这是不可能接受的，整个分析过程会得不到任何有价值的信息。

注：上图是我无耻地粘贴过来的