矩阵相乘Strassen算法Java实现
前言
我们都知道矩阵相乘的规则,矩阵1的m行与矩阵2的n列对应的位置的乘积之和即为结果矩阵m行n列的值,所以只有当矩阵1的列数等于矩阵2的行数时,才可以进行相乘。其实矩阵的本质是线性方程式的表示形式,比如:

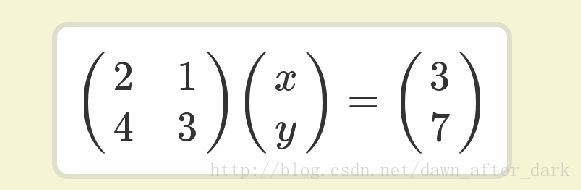
好了,本篇博客重点不在这里。
经典方法
矩阵相乘的经典实现就是按照相乘规则来编写的,三重循环即可
public static void mutipleMatrix(int[][] matrix1, int[][] matrix2,
int[][] result, int row1, int col1, int col2){
for(int i = 0; i < row1; i++)
for(int k = 0; k < col2; k++)
for(int j = 0; j < col1; j++)
result[i][k] += matrix1[i][j] * matrix2[j][k];
}以上方法的复杂度为O(n的三次方),当矩阵维数爆炸时,你的程序一定也会崩溃的,哈哈,下面我们就来看看科学家改进的方法。
Strassen方法
该方法的思想就是分治法,即把一个大问题划分为一个个小问题,对这些小问题逐个击破,分而治之。
一个为2的幂次方的大小为N的矩阵,总是划分为4个大小为N/2的矩阵,所以两个矩阵相乘,又可以是各个分块相乘,虽然这里也是采用了分治法,但是乘法操作还是没有减少,故而复杂度还是没变。看图:

我们发现上诉分治的时候每次乘法操作都是8次,4次加法操作。在计算机中,乘法操作是非常耗时,如果能减少乘法次数,势必会降低复杂度。科学家Strassen就想出了一个方法,通过各种凑数,终于发现可以通过对划分的4个小矩阵进行7次变换,可以减少一次乘法操作。多么牛啊,这就是大神,我佩服。
那么他构造的7个式子是什么呢?看图:

上图中的a,b,c,d…是之前我们划分过得小矩阵。最后的我们可以根据画递归树或者主定理得到复杂度为O(n的2.81次方)!
Java代码
说实话,采用递归实现,每次都要创建一堆的数组,很容易栈溢出的。
package com.special.util;
import java.util.Scanner;
/**
*
* @author special
* @date 2017年12月1日 下午1:31:55
*/
public class StrassenMutipleMatrix {
public static void matrixSub(int[][] matrixA, int[][] matrixB, int[][] result){
for(int i = 0; i < matrixA.length; i++)
for(int j = 0; j < matrixA.length; j++)
result[i][j] = matrixA[i][j] - matrixB[i][j];
}
public static void matrixAdd(int[][] matrixA, int[][] matrixB, int[][] result){
for(int i = 0; i < matrixA.length; i++)
for(int j = 0; j < matrixA.length; j++)
result[i][j] = matrixA[i][j] + matrixB[i][j];
}
public static void Strassen(int N, int[][] matrixA, int[][] matrixB, int[][] result){
if(N == 1){
result[0][0] = matrixA[0][0] * matrixB[0][0];
return;
}
int halfSize = N / 2;
int[][] A = new int[halfSize][halfSize];
int[][] B = new int[halfSize][halfSize];
int[][] C = new int[halfSize][halfSize];
int[][] D = new int[halfSize][halfSize];
int[][] E = new int[halfSize][halfSize];
int[][] F = new int[halfSize][halfSize];
int[][] G = new int[halfSize][halfSize];
int[][] H = new int[halfSize][halfSize];
int[][] C1 = new int[halfSize][halfSize];
int[][] C2 = new int[halfSize][halfSize];
int[][] C3 = new int[halfSize][halfSize];
int[][] C4 = new int[halfSize][halfSize];
int[][] P1 = new int[halfSize][halfSize];
int[][] P2 = new int[halfSize][halfSize];
int[][] P3 = new int[halfSize][halfSize];
int[][] P4 = new int[halfSize][halfSize];
int[][] P5 = new int[halfSize][halfSize];
int[][] P6 = new int[halfSize][halfSize];
int[][] P7 = new int[halfSize][halfSize];
int[][] tempA = new int[halfSize][halfSize];
int[][] tempB = new int[halfSize][halfSize];
for(int i = 0; i < halfSize; i++)
for(int j = 0; j < halfSize; j++){
A[i][j] = matrixA[i][j];
B[i][j] = matrixA[i][halfSize + j];
C[i][j] = matrixA[i + halfSize][j];
D[i][j] = matrixA[i + halfSize][j + halfSize];
E[i][j] = matrixB[i][j];
F[i][j] = matrixB[i][halfSize + j];
G[i][j] = matrixB[i + halfSize][j];
H[i][j] = matrixB[i + halfSize][j + halfSize];
}
matrixSub(F,H,tempB);
Strassen(halfSize,A,tempB,P1);
matrixAdd(A,B,tempA);
Strassen(halfSize,tempA,H,P2);
matrixAdd(C,D,tempA);
Strassen(halfSize,tempA,E,P3);
matrixSub(G,E,tempB);
Strassen(halfSize,D,tempB,P4);
matrixAdd(A,D,tempA);
matrixAdd(E,H,tempB);
Strassen(halfSize,tempA,tempB,P5);
matrixSub(B,D,tempA);
matrixAdd(G,H,tempB);
Strassen(halfSize,tempA,tempB,P6);
matrixSub(A,C,tempA);
matrixAdd(E,F,tempB);
Strassen(halfSize,tempA,tempB,P7);
matrixAdd(P5,P4,C1);
matrixSub(C1,P2,C1);
matrixAdd(C1,P6,C1);
matrixAdd(P1,P2,C2);
matrixAdd(P3,P4,C3);
matrixAdd(P5,P1,C4);
matrixSub(C4,P3,C4);
matrixSub(C4,P7,C4);
for(int i = 0; i < halfSize; i++)
for(int j = 0; j < halfSize; j++){
result[i][j] = C1[i][j];
result[i][j + halfSize] = C2[i][j];
result[i + halfSize][j] = C3[i][j];
result[i + halfSize][j + halfSize] = C4[i][j];
}
}
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner input = new Scanner(System.in);
while(input.hasNext()){
int n = input.nextInt();
int[][] matrixA = new int[n][n];
int[][] matrixB = new int[n][n];
int[][] result = new int[n][n];
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
matrixA[i][j] = input.nextInt();
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
matrixB[i][j] = input.nextInt();
Strassen(n,matrixA,matrixB,result);
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++){
if(j != n - 1) System.out.print(result[i][j] + " ");
else System.out.println(result[i][j]);
}
}
}
}
